дроби »
деление дробей
Деление дробей. Нахождение дроби от числа
Решение: Чтобы выполнить деление дробей, нужно перемножить эти дроби, только при этом перевернув одну дробь наоборот
Например 10/12 :8/11
10 : 8 = 10 * 11 =
12 11 12 8
Теперь выполняем обыкновенное умножение этих дробей
= 10*11 = 110 = 55*2 = 55 = 1 целая 7
12*8 96 48*2 48 48
Чтобы найти дробь от числа, нужно число умножить на эту дробь
например
найти 5/6 от числа 21 число 21 это в виде дроби будет 21/1
21 * 5 = 21 * 5 = 21*5 = 105 = 35*3 = 35 = 17 целых 1
6 1 6 1*6 6 2*3 2 2
можно ещё так сделать решать или проверять
21 * 5/6=21:6*5=3,5(это 3целых 5/10)*5=17целых 5/10=17целых 1/2Деление дробей. Задачи
В детский сад привезли 36кг яблок, груш в полтора раза меньше чем груш сколько всего км фруктов привезли в детский сад
Задача 2
Скорость электрички 50км /ч. На своем маршруте она должна пройти 3 перегона длиной 12км, 15км и 18км сделав при этом 2 остановки 1/20ч сколько потребуется времени на весь маршрут
Решение: 1 ЗАДАЧА:1) Яблоки - 36 кг
Груши - 36/1,5 кг
36/1,5 = 24 (кг) - груш.
2) Груши - 24 кг
Сливы - 24/1,5 кг
24/1,5 = 16 (кг) - слив.
3) 36 + 24 + 16 = 76 (кг) - всего фруктов.
Ответ: было привезено 76 кг фруктов.
2 ЗАДАЧА: Весь путь S - сумма длин перегонов: 12+15+18=45км.
По формуле: V•t=S (скорость умножить на время равно путь) подставим V - скорость и S - путь: 50•t=45, значит время равно 9/10 часа или 18/20 часа (для удобства).
18/20 часа - время движения, но поскольку было совершено две остановки по 1/20ой часа, то суммарное время остановок = 2/20 часа.
Сложим время остановок и время движения электрички: 2/20 часа + 18/20 часа. Получим 20/20 часа или 1 час.
Ответ: время на весь маршрут составит 1 час.Выполнить деление дробей:
2х^ 2+xy-6y^2 / 6х^ 2-5xy+y^2 : 2х^ 2-7xy+6y^2 / 3х^ 2-7xy+2y^2
Решение: $$ \frac{2x^2+xy-6y^2}{6x^2-5xt+y^2} : \frac{2x^2-7xy+6y^2}{3x^2-7xy+2x^2} = $$
По правилам, переворачиваем дробь
$$ =\frac{2x^2+xy-6y^2}{6x^2-5xt+y^2}* \frac{3x^2-7xy+2y^2}{2x^2-7xy+6y^2} = $$
Разложим чилситель и знаменатель дроби на множители
$$ = \frac{(x+2y)(2x-3y)(x-2y)(3x-y)}{(2x-y)(3x-y)(x-2y)(2x-3y)} = $$
Сократим и получаем
$$ = \frac{x+2y}{2x-y} $$
Ответ: $$ \frac{x+2y}{2x-y} $$.
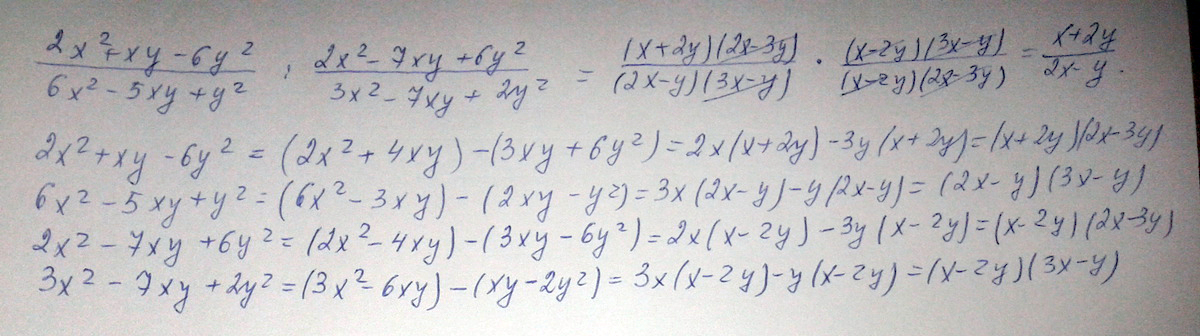
Выполните деление дробей
№1010(1)
а) 3 1/2:2 1/3 в)1 2/3:2 1/2 д)1 5/7:3 3/4
№1011(1)
а) 16/21:20/49 г) 1/4:3 1/2 ж)5:2 1/2 к) 10 1/2:3 1/2
№1022
В одну банку помещается 3/5кг подсолнечного масла. Сколько понадобится банок, чтобы разлить 8кг масла?
Решение: Дроби с целым число переводите в обыкновенную, затем вместо деления ставите знак умножения и переворачиваете вторую дробь вверх ногами и умножаете
№1010 а)=7/2:7/3=7/2*3/7=3/2=1 1/2
в)5/3:5/2=5/3*2/5=2/3
д)12/7:15/4=12/7*4/*15=16/35
№1011 а) =16/21*49/20=28/35=4/5
г) 1/4:7/2=1/4*2/7=1/14
ж) 5/1:5/2=5/1*2/5=2/1=2
к) 21/2:7/2=21/2*2/7=3Тема деление дробей
А) На одной полке 27 книг, а на другой в полтора раза меньше. Сколько книг на двух полках вместе?
б) Привезли 36 яблок, грушь-в полтора раза меньше, чем яблок, а слив в полтора раза меньше чем грушь. Сколько всего фруктов привезли?
Решение: 1 - 27 книг, на второй в 1.5 раза меньше, значит 27/1,5 = 18, 18+27=45.2-36, груши 36/1,5=24, слив 24/1,5 =16
30 меньше 45в полтора раза, также и груши, также и сливы.
То есть делим 36 на полтора, затем 24 на полтора.
А фруктов 76 всего.а) 27/1,5=18 книг
27+18=45 книг в общем
б) 36/1,5=24 груши
24/1,5=16 слив
36+24+16=76 фруктов всего

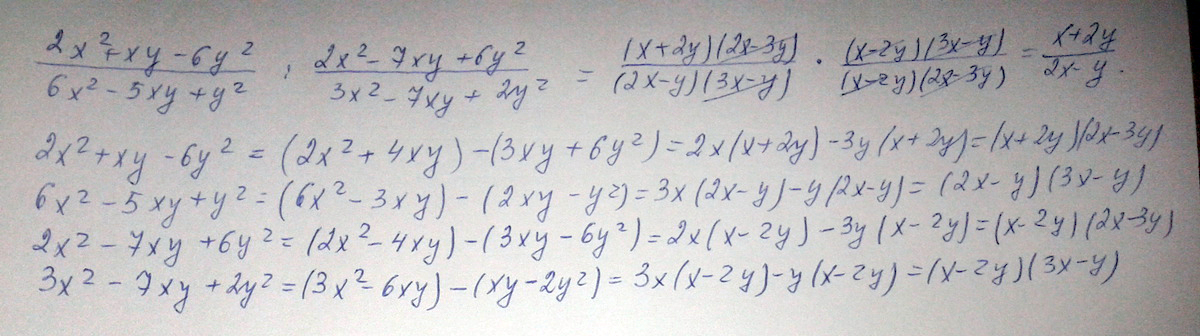
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...