значение какого числа является рациональным
При каких значениях параметра а множеством корней уравнения |x+3|+|x-1|=а является числовой отрезок, длина которого = 4?
Решение: Это задание легко решается графически. Чертим график функции f(x)=|x+3|+|x-1|
График функции а представляет собой прямую, параллельную оси ох
Мы ищем промежуток в графике модуля, где расстояние между ветвями равно 4
Видим, что только при а=4 промежуток равен 4, дальше идет увеличение промежутка, а при а<4 решений нет.При каких значениях параметра а множеством корней уравнения |x+3|+|x-1|=а является числовой отрезок, длина которого = 4 ?
Решим данное уравнение аналитически по методу интервалов
Найдем точки смены знаков выражений под модулями |x+3| и |x-1|
х+3=0 и х-1 = 0
х=-3 х=1
Получили три области (-бескон;-3];[-3;1];[1;+бескон)
В первом интервале (-бескон;-3]
х+3<0 и х-1<0
Поэтому Ix+3I=-x-3 и Ix-1I=1-x
Запишем уравнение
Ix+3I+Ix-1I =a
-x-3 +1-x=a
a=-2х-2 или х=(-a-2)/2
Так как х принадлежит (-бескон;-3] то a принадлежит [4;+бескон)
Решением на этом отрезке является одна точка
На интервале [-3;1]
х+3>0 и х-1<0
Поэтому Ix+3I=x+3 и Ix-1I=1-x
Запишем уравнение
Ix+3I+Ix-1I =a
x+3+1-x=a
4=a
Поэтому при а=4 решением является множество х принадлеж [-3;1]
На интервале [1;+бескон)
х+3>0 и х-1>0
Поэтому Ix+3I=x+3 и Ix-1I=x-1
Запишем уравнение
Ix+3I+Ix-1I =a
x+3+x-1 =a
a=2x+2 или х =(а-2)/2
Так как х принадлежит [1;+бескон) то a принадлежит [4;+бескон)
Решением на этом отрезке является одна точка
Следовательно решением данного уравнения при a>4 являются два значения
х =(а-2)/2 и х=-(а+2)/2
При а=4 множество значений х принадлежащих [-3;1] длинной =4
При a<4 решений данное уравнение не имеет.
Ответ: при а=41 Вычислите дискриминант квадратного трёхчлена: a)3x^2-8x+5; б)x^2-16x+64 2 Разложите квадратный трёхчлен на линейные множители a)x^2-4x+3; б)3x^2-2x-5 5При каком значении а число 3 является корнем квадратного трёхчлена x^2-2x+a?
Решение: 1. а. Д=(-8)^2-4*3*5=4б. Д= (-16)^2-4*64=0
2.а. x^2-4x+3=1(х-1)(х-3)=(х-1)(х-3)
Д=16-4*3=4
х1= (4+2)/2=3
х2=(4-2)/2=1
Ответ: (х-1)(х-3)
б. 3x^2-2x-5=3(х+1)(х-5/3)=(х+1)(3х-5)
Д=4-4*3*(-5)=8^2
х1=(2-8)/6=-1
х2=(2+8)/6=5/3
Ответ: (х+1)(3х-5)
1.
а) Д=64-4*3*5=64-60=4
б) Д=256-4*1*64=256-256=0
2.
а)Д=16-4*1*3=16-12=4
корень из Д= 2
х1=6/2=3
х2=2/2=1
х^2-4x+3=(x-3)(x-1)
б)Д=4-4*3*(-5)=4+60=64
корень из Д=8
x1=10/2=5
x2=-6/2=-3
3x^2-2x-5=3(x-5)(x+3)
1) Корни уравнения x^2+16x+a=0 относятся как 4:3. Найдите значение a и корни уравнения.2) Найдите, не вычисляя значения дискримината, при каком значении a уравнение имеет единственный корень. Найдите эти корни.
А) x^2+20x+a=0
Б) x^2+ax+25=0
3) При каком значении m корни уравнения x^2+mx-11=0 являются противоположными числами? Найдите эти корни.
Решение:$$ 1)\; x^2+16x+a=0\\ \frac{x_2}{x_1}= \frac{4}{3} \; ,\; \; x_2=\frac{4x_1}{3}\\x_1+x_2=-16\; \; \to \; \; x_1+\frac{4x_1}{3}=-16\; ,\; \frac{7}{3}x_1=-16\; ,\; x_1=-\frac{48}{7}\\x_2=-\frac{4\cdot 48}{3\cdot 7}=-\frac{64}{7}\\a=x_1\cdot x_2=\frac{48}{7}\cdot \frac{64}{7}=\frac{3072}{49}=62\frac{34}{49} $$
$$ 2)\; \; a)\; \; x^2+20x+a=0\\D/4=10^2-a=0\; \; \to \; \; a=100\\b)\; \; x^2+ax+25=0\\D=a^2-100=0\\a=\pm 10\\3)\; \; x^2+mx-11=0\; ,\; \; x_1=-x_2\\x_1\cdot x_2=-11\; \; \to \; \; (-x_2)\cdot x_2=-x_2^2=-11\\x_2=\pm \sqrt{11}\\x_1=\mp \sqrt{11}\\-m=x_1+x_2=(-x_2)+ x_2=0\\m=0 $$№1 Является ли пара чисел (3:-4) решением системы а) {2х+у=2 {5х вторая степень +5ху+у вторая степень=х+у
б){7х+5у=1 {1-ху=-11
№4 найдите значение выражения 2х+5у, если х-2у=15 и 2х+3у=16
№5 при каких значениях а и b решением системы {2х-ау=b-2 является пара чисел (2:-3) {ах-3у=b+2
№9 вычислите координаты точки пересечения прямых а) у=2х-4 и у=-3х+1 б)4х-3у=-1 и 3х+2у=12
Решение: 1. а) 6 + y = 2y = -4 -- подходит.
45 +15y + y^2 = 3 + y
45 + (-60) + 16 = 3 - 4
1 = - 1 -- не подходит. значит пара чисел (3; -4) не подходит.
б) 21 + 5y = 1
y = -4 -- подходит
1 - 3y = - 11
13 = - 11 -- не подходит. то же самое.
4. 2(2y + 15) + 5y = 9y + 30
16 - 3y + 5y = 16 + 2y
9y + 30 = 16 + 2y
7y = - 14
y = - 2
x = 15 + 2y = 15 - 4 = 11
5. 4 + 3a = b - 2
2a + 9 = b + 2 -- система
3a = b - 6
2a = b - 7 -- система. вычитаем из первого второе
a = 1
значит, b = 9
9. а) 2x - 4 = - 3x + 1
5x = 5
x = 1
подставим. y = 2 - 4 = - 2
б) y = 1/3 + 4/3 * x
y = 6 - 3/2 * x
1/3 + 4/3 * x = 6 - 3/2 * x
19/6 * x = 6
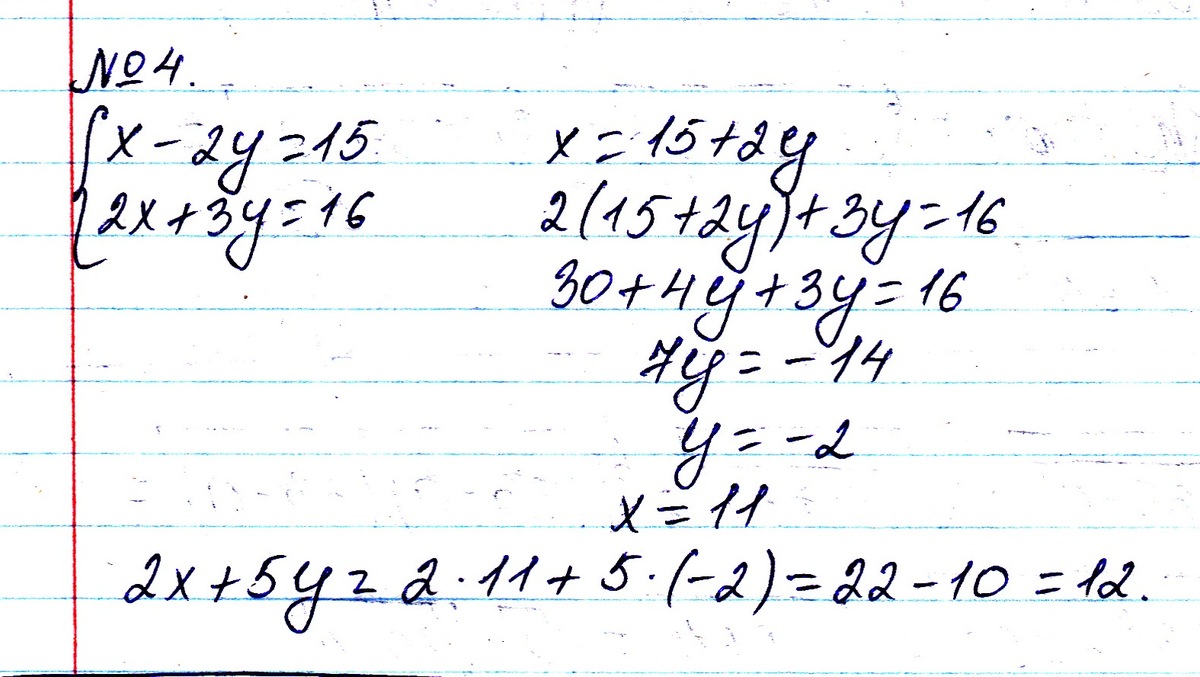
1. Верно ли, что если число рациональное, то оно является целым?
2. Каждое ли число является рациональным?
3. Что называют модулем числа?
4. Какие значения может принимать модуль числа?
5. Чему равен модуль положительного числа?
6. Чему равен модуль числа 0?
7. Чему равен модуль отрицательного числа?
8. Что можно сказать о модулях противоположных чисел?
Решение:
1. нет (например 1,2 - число рациональное, но не целое)
2. нет (√3 -число иррациональное)
3. Это расстояние от координаты до начала отсчёта
4. Неотрицательны (положительные и ноль)
5. самому числу
6. нулю
7. противоположному числу
8. модули противоположных чисел равны

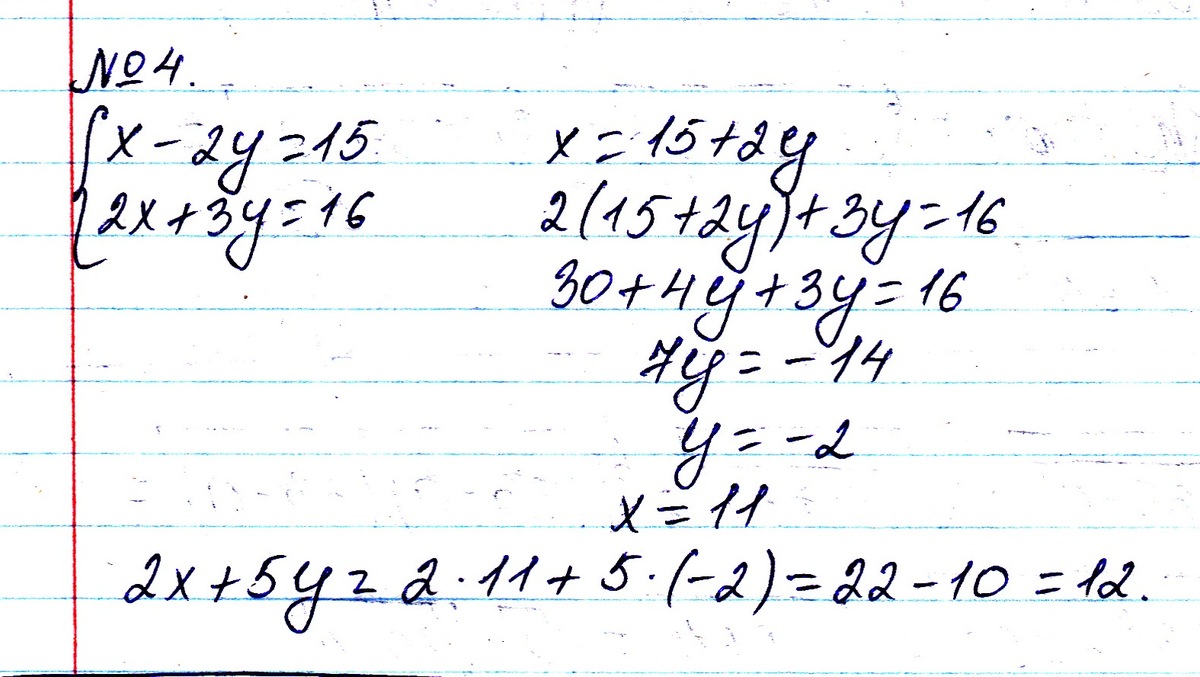
 Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...
Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...