график функции »

график касательной к функции

  • 1. Найти сумму целых решений неравенства \( (x-1)(x+2)(x-4) ^{2} \leq 0 \)
    2. Укажите абсциссу точки графика функции \( y=5+4x- x^{2} \), в которой угловой коэффициент касательной равен 3
    3. Найти наибольшее значение функции \( y=2,7*e ^{3 x^{2} - x^{3}-4 } \) на отрезке [1;3]
    4. Вычислите \( (3,4 \sqrt[3]{25 \sqrt{5} }+1,6 \sqrt{5 \sqrt[3]{25} } ^{ -\frac{6}{11} } \)


    Решение: 1.
    $$ (x-1)(x+2)(x-4) ^{2} \leq 0, \\ (x-1)(x+2)(x-4) ^{2} = 0, \\ x_1=-2, x_2=1, x_3=4, \ (x-4) ^{2} \geq 0, (x-1)(x+2) \leq 0, \\ -2 \leq x \leq 1, \ x\in[-2;1]\cup\{4\}; -2+(-1)+0+1+4=2. $$
    2.
    $$ y=5+4x- x^{2}, k=y’_{x_0}=3, \\ y’=4-2x, \\ 4-2x_0=3, \\ x_0=0,5. $$
    3.
    $$ y=2,7e ^{3 x^{2} - x^{3}-4 }, x\in[1;3], \\ y’=2,7e ^{3 x^{2} - x^{3}-4 }\cdot(6x-3x^2), \\ y’=0, \\ 8,1e ^{3 x^{2} - x^{3}-4 }\cdot x(2-x)=0, \\ e ^{3 x^{2} - x^{3}-4 }>0, \\ \left[ {{x=0,} \atop {x=2;}} \right. $$
    $$ x=1, y=2,7e ^{3\cdot1^{2}-1^{3}-4}=2,7e^{-2}, \\ x=2, y=2,7e ^{3\cdot2^{2}-2^{3}-4}=2,7 \\ x=3, y=2,7e ^{3\cdot3^{2}-3^{3}-4}=2,7e^{-4}, \\ \max\limits_{x\in[1;3]}y=2,7;\min\limits_{x\in[1;3]}y=2,7e^{-4}. $$
    4.
    $$ (3,4 \sqrt[3]{25 \sqrt{5} }+1,6 \sqrt{5 \sqrt[3]{25} }) ^{ -\frac{6}{11} } = (3,4 \sqrt[3]{5^2 \sqrt{5} }+1,6 \sqrt{5 \sqrt[3]{5^2} }) ^{ -\frac{6}{11} } = \\ = (3,4 \sqrt[3]{ \sqrt{5^4\cdot5} }+1,6 \sqrt{ \sqrt[3]{5^3\cdot5^2} }) ^{ -\frac{6}{11} } =(3,4 \sqrt[6]{ 5^5}+1,6 \sqrt[6]{5^5 }) ^{ -\frac{6}{11} } = \\ = (5\sqrt[6]{5^5 }) ^{ -\frac{6}{11} } = (5\cdot5^{ \frac{5}{6} }) ^{ -\frac{6}{11} } = (5^{ \frac{11}{6} }) ^{ -\frac{6}{11} } =5^{-1}= \frac{1}{5}= 0,2. $$

  • Определите какой угол образует с осью х касательная,проведенная к графику функций y=f(x) в точке с абсциссой х=а,если
    1) f (x)=-3х(в кубе),а=1\3
    2) f (x)=0,2x(в 5 степени),а=-1
    3) f (x) =- 0,25x(в 4 степени), а=0
    4) f (x) = -7x(в кубе)+10х(в квадрате) +х-12, а=0
    5) f (x)= 2x-1\3-2x,a=1\2
    6) f (x)=x-1\x-2, a=1


    Решение: 1) f (x)=-3х³,а=1\3
    f`(x)=-9x²  f`(1/3)=-9*1/9=-1  tga=-1  a=135
    2) f (x)=0,2x(в 5 степени),а=-1
    f`(x)=x^4  f`(-1)=1  tga=1  a=45
    3) f (x) =- 0,25x(в 4 степени), а=0
    f`(x)=-x³  f`(0)=0  tga=0  a=0
     4) f (x) = -7x³+10х² +х-12, а=0
    f`(x)=-21x²+20x+1  f`(0)=1  tga=1  a=45
     5) f (x)= 2x-1\3-2x,a=1\2
    f`(x)=(6-4x+4x-2)/(3-2x)²=4/(3-2x)²  f`(1/2)=4/4=1  tga=1  a=45
     6) f (x)=x-1\x-2, a=1
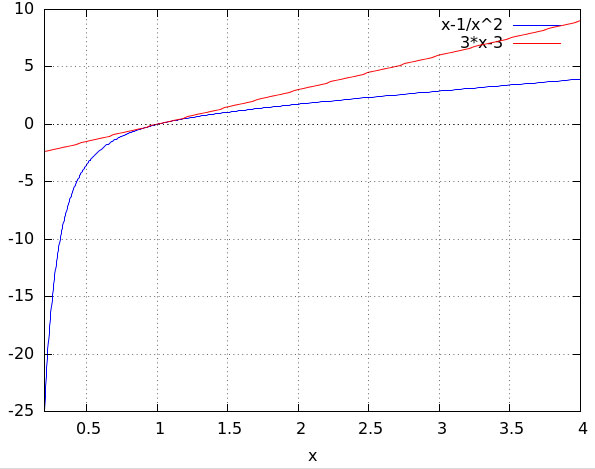
    f`(x)=(x-2-x+1)/(x-2)²=-1/(x-2)²  f`(1)=-1/1=-1  tga=1  a=135




  • Является ли прямая y=3x-3 касательной к графику функции y=x-1/× (X во второй степени)


    Решение:


    $$ f(x)=x- \frac{1}{x^2} $$ функция
    $$ y(x)=3x-3 $$ прямая
    Не знаю как учили это решать. Попробую объяснить как я рассуждал.
    Чтобы уравнение прямой являлось уравнением касательной в некоторой точке x0 должны выполняться соотношения:
    $$ f(x_{0})=y(x_{0}) $$ (3)
    $$ f^{’}(x_{0})=y^{’}(x_{0})=k $$ (4)
    Напоминаю, что общий вид одного из видов уравнений прямой
    $$ y(x)=k*x+b $$
    У нас к=3, вот от этого пляшем
    $$ f^{’}(x)=1+2 \frac{1}{x^3} $$
    Приравниваем эту производную к 3 и смотрим есть ли вообще такие точки, где (4) выполняется
    $$ f^{’}(x)=1+2 \frac{1}{x^3}=3 $$
    $$ \frac{1}{x^3}=1 $$
    $$ x^{3} =1 \\ x=1 $$
    Есть, хорошо проверяем (3)
    $$ f(1)=1-\frac{1}{1^2} =1-1=0 \\ y(1)=3*1-3=0 $$
    условия выполнены, значит данное уравнение прямой, является уравнением касательной для функции f(x) в точке с координатами(1;0)

    f x x- frac x функция y x x- прямаяНе знаю как учили это решать. Попробую объяснить как я рассуждал.Чтобы уравнение прямой являлось уравнением касательной в некоторой точке...

  • На оси y взята точка В, из неё проведены касательные к графику функции y=3-0,5x². Известно, что эти касательные образуют между собой угол 90°. Найдите координаты точки В


    Решение: Y=3-x^2/2
    Берем производную
    y’=-x
    Чертим параболу. Она симметрична
    Т. к. угол равен 90 градусов, то угол между касательными и осью ОХ равен 45 град
    tga=y’
    tg45=1 => 1=-x => x=-1
    Находим значение функции в этой точке
    y(-1)=3-0.5=2.5
    Находим уравнение касательной в этой точке
    y’(-1)=1
    y=f(a)+f’(a)(x-a)=2.5+1(x+1)=x+3.5
    Точка пересечения двух касательных (0; 3.5)

  • На оси y взята точка B, из нее проведены касательные к графику функции \( y=3- \frac{1}{2} x^{2} \) Известно, что эти касательные образуют между собой угол 90 градусов. Найдите координаты точки B


    Решение: Касательная прямая есть производная в точке.
     Пусть точка касания с графиком имеет координаты $$ A(x_{1};y_{1}) $$. 
     График функций $$ y=3-\frac{x^2}{2} $$ симметричен относительно оси $$ oY $$. Пересекающая ось $$ oY $$ в точке $$ f(0)=3 $$.
    Очевидно что координата точки $$ B(x_{2};y_{2})\\ y_{2}>3 $$.
    Рассмотрим прямоугольный треугольник образованный касательной к графику функций с осями ординат и абсцисс. 
      $$ f’(x)=tga $$. Так как график симметричен, то угол образующие касательные $$ 90а $$, ордината будет являться биссектрисой. Следовательно треугольник будет прямоугольным и равнобедренным. 
    пусть касательная имеет вид $$ y=kx+b \\ y’=(3-\frac{x^2}{2})’=-x\\ -x=1\\ x=-1 $$, так как $$ tg45а=1 $$ 
    Точка касания равна -1, касательная в этой точке по формуле 
     $$ f(-1)=\frac{5}{2}\\ f’(-1)=1\\\\ y=\frac{5}{2}+1(x+1)=x+\frac{7}{2}\\ $$
    То есть координата $$ B(0;\frac{7}{2})=B(0; \ 3,5) $$

  • К графику функции y=x^2+2x-3 проведены касательные в точках (0;-3) и (-2;-3). Найдите координаты точки пересечения этих касательных


    Решение: Yk = f(xo)+f’(xo)(x-xo).
    1) xo(0;-3).
      f(xo) = -3.
      f’(x) = 2x+2.
      f’(xo) = 2*0+2 = 2
      yk = -3+2(x-0) = 2x-3.
    2) xo(-2;-3).
      f(xo) = 4-4-3 = -3.
      f’(x) = 2x+2.
      f’(xo) = -4+2 = -2
      yk = -3-2(x+2) = -3-2x-4 = -2x-7.
    Точка К пересечения: 
      2х-3 = -2х-7
      4х = -4
      х = -4/4 = -1.
      у = 2*(-1)-3 = -2-3 = -5.
      К(-1; -5). 

    Yk f xo f xo x-xo . xo - .  f xo - .  f x x .  f xo   yk - x- x- .  xo - - .  f xo - - - .  f x x .  f xo - -   yk - - x - - x- - x- .Точка К пересечения    х- - х-   х -   х...

  • К графику функции у=корень (х+2) проведена касательная, образующая с осями координат треугольник наименьшей площади. Найдите координаты точки касания.


    Решение: D(y)=[-2;+∞)- область определения данной функции.
    Cоставим уравнение касательной к кривой в точке z
    y(z)=√(z+2);
    y’(x)=1/2√(x+2)
    y`(z)=1/2√(z+2)
    Уравнение
    у-у(z)=y’(z)(x-z)
    y-√(z+2)=(x-z)/2√(z+2)
    Найдем точки пересечения касательной с осями координат
    При х=0  у=√(z+2)-(z/2√(z+2))=(2z+4-z)/2√(z+2)=(z+4)/2√(z+2)
    При у=0  x-z=-2(z+2)  ⇒x=-z-4
    Треугольник, образуемый касательной с осями координат- прямоугольный, с катетами |-z-4|  и |(z+4)/2√(z+2)|
    Площадь прямоугольного треугольника находим по формуле как  половину произведения катетов:
    S(Δ)=(1/2)|-z-4|·(z+4)/2√(z+2)=(z+4)²/4√(z+2)
    S’(z)=2(z+4)(3z+4)/16(z+2)√(z+2)
    S’(z)=0
    3z+4=0
    z=-4/3
    y(-4/3)=√((-4/3)+2)=1/√3
    О т в е т.(-4/3; 1/√3)

  • Дана функция f(x)=3+5x+3x^2. Найдите координаты точки её графика, в которой угловой коэффицент касательной к нему равен -7.


    Решение: касателная  ест  производной  функции  в точке.

     производная :

    (3+5x+3x²)’  = (3)’+(5x)’+(3x²)’  =  0 + 5 + 3 · 2x =  6x + 5

     искаем  аргументу  для которрого    6x + 5 = (-7)

     6x =( -7 ) -5 = -12

     x= (-2)

     тепер   найдем значение функцйии для этого аргумента

    y= 3+5x+3x²    где  x = (-2)  

    y= 3 + 5 · (-2) +  3 · (-2)²  = 3 + (-10) + 3· 4 = (-7) + 12=  5

    искана  точка, т=  ((-2), 5 )

     во вложению  граф, 

    касателная  y = (-7) x  +  C   по поводу  grafa  найдем  число  C

    5 = (-7)· (-2)+ C

    C= 5 - 14 = -9

    касателна  в точке  (-2, 5)  :    y= (-7) x - 9

    извините  лексикальное  граматические ошибки  я не русский

  • Найдите площадь треугольника, ограниченного осями координат и касательной к графику функции f(x)=кореньиз(5-4х), проведенной в точке его пересечения с прямой у=х.
    Решите с подробным объяснением


    Решение: Найдем точку пересечения графиков заданных функций:
    {y=√(5-4x)
    {y=x √(5-4x)=x; 5-4x=x^2; x^2+4x-5=0; x1=-5;x2=1
      x1=-5; √(5+20)=-5 неверно! 
      x2=1; √(5-4)=1 верно, х=1-корень уравнения
    тогда у=1, (1;1)-точка пересечения
    Составим уравнение касательной: f(x)=f(a)+f’(a) *(x-a); а=1
    f(1)=√(5-4*1)=1;
    f’(x)=(√(5-4x))’=1/(2√(5-4x)) *(5-4x)’=-4/ (2√(5-4x))=-2/√(5-4x);
    f’(1)=-2/√(5-4)=-2
    f(x)=1-2*(x-1); f(x)=-2x+2-уравнение касательной
    Найдём точки пересечения касательной с осями координат
    с осью х: y=0; -2x+2=0; -2x=-2; x=1
    с осью у: x=0; y=-2*0+2; y=2
    тогда имеем прямоугольный треугольник с катетами, длины которых1 и2
    S=1/2 *1*2=2/2=1
    Ответ. 1

  • 5) Найдите площадь треугольника, образованного осями координат и касательной к графику функции f (х) = 3х-2(корень из) х в точке с абсциссой х0 = 4


    Решение: Найдем уравнение касательной,  по формуле
      $$ y=f(a)+f’(a)(x-x_{0}) $$ 
     $$ f(4)=3*4-2\sqrt{4}=8\\ f’(x)=3-\frac{1}{\sqrt{x}}\\ f’(4)=3-\frac{1}{2}=\frac{5}{2}\\\\ y=8+\frac{5}{2}(x-4) = \frac{5x}{2}-2\\\\ $$
    Точки пересечения прямой с осями координат, равны 
    $$ OX=>\frac{5x}{2}-2=0\\ x=\frac{4}{5}\\ |OY|\\ => \frac{5*0}{2}-2=|2|\\\\ S=\frac{\frac{4}{5}*2}{2}=\frac{4}{5} $$

1 2 > >>