график функции »

точки пересечения графика функции - страница 2

  • Линейная функция y=2x+8 найдите:
    а). наименьшее и наибольшее значение функций на отрезке [-2;1 ]
    б). координаты точки пересечения графика функции с осью Ox


    Решение: Функция возрастающая, поэтому большему значению аргумента соответствует большее значение функции.
    У=2х+8
    У=2(-2)+8=4
    Это наименьшее значение.
    У=2*1+8=10 наибольшее значение.
    б) при пересечении с осью ОХ координата у=0
    0=2х+8
    Х= -4
    А(-4;0) точка пересечения прямой
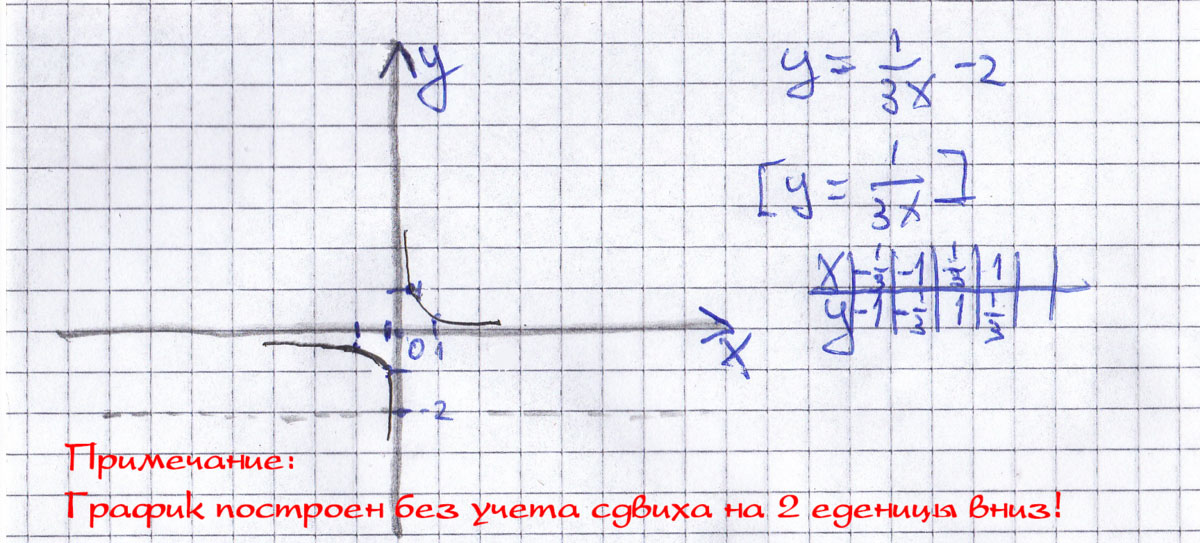
    с осью ОХ

  • Постройте график функции y=1/3x-2. Найдите
    А) наименьше и наибольшее значения функции на отрезке [0;3]
    Б) координаты точки пересечения графика функции с осью Ox


    Решение: График ф-ии будет прямая. Наименьшее значение на заданном тобой отрезке будет при х=0, т. е.2, а наибольшее при х=3, т. е.1. Координата (она будет одна) точки пересечения будет [6,0].

    Графиком функции является гипербола. В в точке [x = 0], "y" не существует, так как на ноль делить нельзя. "y" наименьшее  =  - 17/9 ≈ -1.8888888. (8);

    График ф-ии будет прямая. Наименьшее значение на заданном тобой отрезке будет при х т. е. а наибольшее при х т. е. . Координата она будет одна точки пересечения будет . Графи...

  • дана функция f:R к R найдите точки пересечения графика функции с осями координат если, f(x)= - 3,2x - 6,4


    Решение: Определяем точку пересечения графика с ос. иксов, f(x)=0(тоесть ордината этой точки равна нулю). Получаем уравнение6 -3,2х-6,4=0,3,4х=6,4, х=6.4:(-3,2).

    х=-2. (-2;0) это точка пересечения с ос. абсцисс(иксов).

    Определяем точку пересечения с ос. ординат(игреков). Для этой точки х=0,

    f(0)=-3,2·0-6,4=-6,4. (0;-6,4) это точка пересечения с ос. ординат(игреков).

    Ответ: (-2;0), (0;-6,4). 

  • определите точки пересечения графика функции y=-2x+7 с осями координат


    Решение: График пересекается с осью Ох при х=0, при этом у=-2*0+7=7, точка пересечения с осью Ох имеет координаты (0;7)

    График персекается с осью Оу при у=0, при этом х=(0-7)/-2=3,5, Точка пересечения с осью Оу имеет координаты (3,5;0)

    Надо посмотреть при каких значениях х, у будет = 0, и при каких значениях у, х будет = 0.

    Итак, если х=0, то у=7

    если х=3,5, то у=0

    значит, точка пересечения с ОУ - 7, а с ОХ - 3,5

    Для наглядности можно построить график

  • Определите точки пересечения графика функции y=2x-3c с осями координат


    Решение: Тогда сперва y=0 и решаете уравнение, а потом х=0 и решаете второе уравнение. в первом случае вы получите точку пересечения оси x, а во втором точку пересечения оси y.

    Y=2x-3
    1) С осью Ох (у=0)
      2х-3=0
      2х=3
      х=1,5
      (1,5;0) - искомая точка
    2) С осью Оу (х=0)
      у(0)=2*0-3=0-3=-3
      (0;-3) - искомая точка
    Ответ: (1,5;0) и (0;-3)
     

<< < 12 3 > >>