график функции »
найдите абсциссы точек пересечение графика
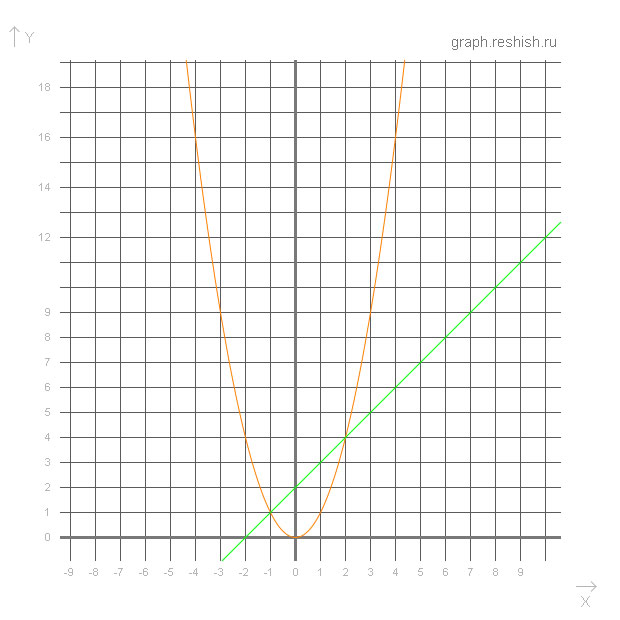
В одной системе координат (единичный отрезок 1 см)постройте график функции y=x^2 ,y=x+2 и найдите абсциссы их точек пересечения.
Решение: Для того, чтобы найти точки пересечения графиков функций f(x) и g(x), надо решить уравнение f(x) = g(x).
В данном случае это будет уравнение x² = x + 2. Решаем это уравнение:
x² = x + 2
x² - x - 2 = 0
x1 = -1; x2 = 2 (по теореме Виета о корнях приведённого квадратного уравнения)
Ответ: абсциссы точек пересечения графиков -1 и 2.
Вычислить длину дуги линии между точками пересечения с осью Оу
(9y^)=4(3-x)^3
Решение: Заданная кривая имеет 2 симметричные относительно оси Х ветви.
Пределы измерения по оси Х - от 0 до 3.
Преобразуем функцию 9y²=4(3-x)³:
$$ y= \frac{2}{3}(3-x)^{ \frac{3}{2} }. $$
Производная этой функции равна:
$$ y’=- \sqrt{3-x}. $$
Длина дуги равна:
$$ L=2* \int\limits^3_0 {(1+3-x)} \, dx =2* \int\limits^3_0 ({4-x}) \, dx $$ = 2*((-2/3)*(4-x)^(2/3)|₀³ = 2*((-2/3)-(-16/3)) = 28/3 = 9(1/3).
Отметьте на координатной плоскости точки Т(5,4), К(-1,2). Постройте прямую Т1 К1 симметричную прямой Т К относительно оси абсцисс. Найдите координаты точек пересечения прямой Т1 К1 с осью абсцисс.
А) (-6,0) В) (0,7) С) (0, 2,5) Д) (2,5, 0)
скиньте фотку. И букву ответа .
Решение: T1(5;-4) K1(-1;-2)
A(-6;0)
Отметьте на координатной плоскости точки Т(5,4), К(-1,2). Постройте прямую Т1 К1, симметричную прямой Т К относительно оси абсцисс. Найдите координаты точек пересечения прямой Т1 К1 с осью абсцисс
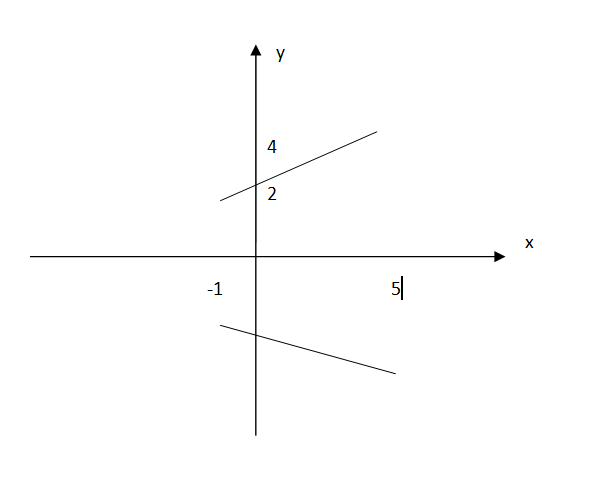
SOS Желательно .
Дана функция f(x)=6-5x-x^2. Не производя построения графика, найдите:
а) координаты точек пересечения графика с осью абсцисс.
б) координаты точки пересечения графика с осью ординат.
в) координаты точек пересечения графика с прямой y=5x+6
г) наибольшее значение функции.
Решение: А) пересечение с осью абсцисс, это f(x)=0
6-5x-x^2=0
X=-2
X=3
Две точки: A(-2;0), B(3;0)
Б) пересечение с осью ординат, это x=0
f(x)=6
Значит точка C(0;6)
В) пересечение с графиком функции, нужно их уравнять
6-5x-x^2=5x+6
X=0 и x=-10
Значит точки с координатами (0;6) и (-10;10)
Г) график функции-парабола, ветви направлены вниз, значит наибольшее значение функции это вершина
Xвершины=5:-2=-2,5
Yвершины=12,25
Наибольшее значение функции 12,25
Парабола задана уравнением y=x^2-4x-5a) Найдите координаты вершины параболы. б) определите, куда(вверх, вниз) направленны ветви параболы, и объясни почему. в) Найдите координаты точек пересечения параболы с осью абсцисс. 2. Найдите наименьшее значение функции y=x^2-4x-5.
Решение: а) Координаты вершины:
х0=-b/2ax0=-(-4)/2*1=4/2=2
y0=x^2-4x-5a
y0=2^2-4*2-5=4-8-5=-9
Координаты вершины: (2;-9)
б) Ветви параболы направлены вверх, т. к. а=1 (т. е. он больше нуля)
y=a^2-bx-c -это общий вид квадратного уравнения. И вот этот первый коэффициент а=1.


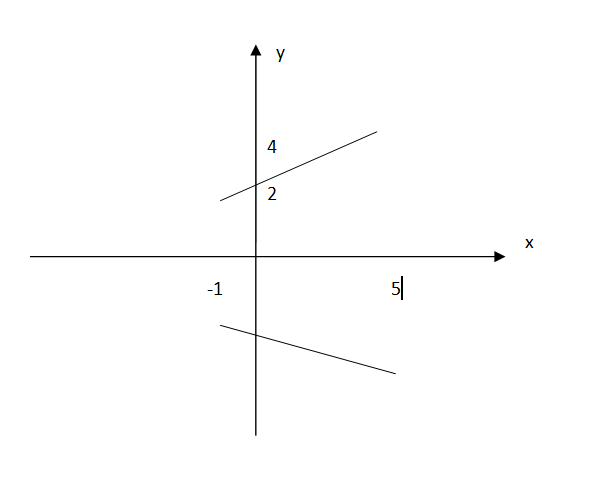
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...