координаты »
найти координаты середины отрезка
Найти координаты середины отрезка АВ, если А (5;1) и В (1;5).
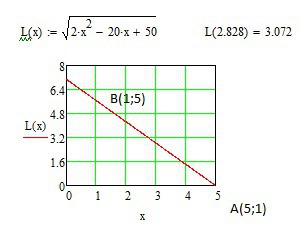
Решение: Длина отрезка АВ составляет√ ((ха-хв)²+(yа-yв)²)=5,6657 единиц, соответственно половина длины составляет 2,828 единиц. Уравнение отрезка АВ имеет вид прямой с отрицательным угловым коэффициентом k=-(ха-хв)/(yа-yв)=-1 (направлен из верхнего левого угла в правый нижний).
yab=-x+6. Расстояние от точки А до середины L=√((хц-5)²+(-хц+6-1)²)=√((хц-5)²+(5-хц)²)=2*хц²-20*хц+50. График расстояния от точки А показан на рисунке. Середине отрезка соответствует хц=3, L(хц)=yц=3.072.
Данные точки А (4,8) В (2,2)
а) найти координаты середины отрезка АВ
б) найти длину АВ
в) определите, какая из данных точек принадлежит прямой x-y+4=0
Решение: 1) (4+2)\2=3
(8-2)\2=3
Значит, координаты середины отрезка (3;3). 1 строчка - находим х, 2 строчка - находим у. Мы к координате А прибавляем координату В.
2) АВ= корень из( (2-4)^2 +(-2-8)^2))= корень из (4 + 100) = корень из 104= 2 корня из 26
3) Проверим А: 4+8=4 - неверно, значит А не принадлежит
Проверим В: 2+2=4 - верно, значит В принадлежитКонцы отрезка CD имеют координаты C(-4:3),D(4;-3). НАйти координаты середины отрезка CD.
Решение: Координаты середины этого отрезка (0;0).
О (хО;yO) - середина отрезка CD
xO= (xC+xD)/2
yO=(yC+yD)/2
C(-4:3), D(4;-3)
xO= (-4+4)/2=0
yO=(3-3)/2=0
Теперь правильно
Теорема Пифагора:
длина отрезка=
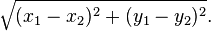
Даны точки А и В А (1;-3;0) В (-2;-4;1) найти координаты середины отрезка АВ найти длину отрезка АВ
Решение: Пусть точка С является точкой середины отрезка АВ, тогда найдем координаты точки С:
$$ C=(\frac{1+(-2)}{2}; \frac{-3+(-4)}{2}; \frac{0+1}{2})=(\frac{1-2}{2}; \frac{-3-4}{2}; \frac{0+1}{2})=(\frac{-1}{2};\frac{-7}{2}; \frac{1}{2})=(-\frac{1}{2}; -3\frac{1}{2}; \frac{1}{2}) $$
Теперь найдем длину отрезка АВ
$$ AB=\sqrt{(1-(-2))^2+(-3-(-4)^2+(0-1)^2}=\sqrt{(1+2)^2+(-3+4)^2+(0-1)^2}=\\=\sqrt{3^2+1^2+(-1)^2}=\sqrt{11} $$Найдите формулу для определения координаты середины отрезка
Решение: Координаты середины отрезка через координаты радиус-векторов его концов. Формулы для нахождения координат середины отрезка легко получить, обратившись к алгебре векторов. Пусть на плоскости задана прямоугольная декартова система координат Oxy и точка С – середина отрезка АВ, причем и. По геометрическому определению операций над векторами справедливо равенство (точка С является точкой пересечения диагоналей параллелограмма, построенного на векторах и, то есть, точка С – середина диагонали параллелограмма). В статье координаты вектора в прямоугольной системе координат мы выяснили, что координаты радиус-вектора точки равны координатам этой точки, следовательно, Тогда, выполнив соответствующие операции над векторами в координатах, имеем. Откуда можно сделать вывод, что точка С имеет координаты. Абсолютно аналогично могут быть найдены координаты середины отрезка АВ через координаты его концов в пространстве. В этом случае, если С – середина отрезка АВ и, то имеем.А(х1: у1) иВ(х2: у2)
Х=(х1+у1)/2
У=(х2+у2)/2


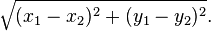
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...