координаты »
как найти координаты вектора
В прямоугольной системе координат Охуz построить точки A (5,-1,3), B (2, -2,4). Найти координаты вектора AB.
Решение: Использовано определение координат точки в прямоугольной системе координат XOYZ, определение координат вектора, применена формула координат вектора через координаты его начала и конца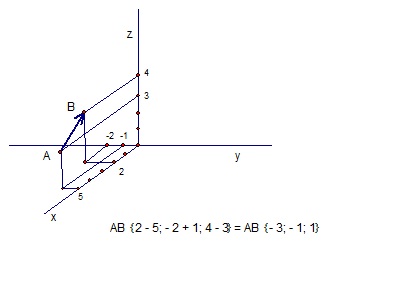
Даны координаты вершин пирамиды ABCD: A(-1;1;-5) В(3;5;-7) С(1;12;-15) D(-1;3;-4) Необходимо:
1.Записать векторы АВ, АС, АD в ортонормальной системе {i,j,k} и найти модули этих векторов.
2.Найти угол между векторами АВ и АС
3.Найти проекцию вектора AD на вектор АВ
4.Вычислить площадь грани АВС
5.Найти обьем пирамиды АВСD
Решение: 1.AB=(3-(-1));(5-1);(-7-(-5))=(4;4;-2)=4i+4j-2k AC=(1-(-1));(12-1);(-15-(-5))=(2;11;-10)=2i+11j-10k AD=(-1-(-1));(3-1);(-4-(-5))=(0;2;1)= 2j+k Модули векторов. |AB|=sqrt (все под корнем)4^2+4^2+2^2=sqrt36=6 |AC|=sqrt 2^2+11^2+10^2=sqrt225=15 |AD|=0^2+2^2+1^2=sqrt 5=2,236
2. угол между АВ и АС : cosy=4*2+4*11+(-2)*(-10)/6*15=0,8 y=arccos (0,8)=36,871°
3.проекция вектора:Ррав АС=2*4+11*4+(-10)*(-2)/sqrt 36=12
4.площадь грани cosy =sqrt 1-0,8^2=0,6 площадь грани АВС :Sавс=1/2|АВ|*|АС|siny=1/2 sqrt 36*sqrt 225 * 0,6 =27
5. Объем пирамиды | 4 4 -2 | V=1/6 | 2 11 -10 |=108/6 | 0 2 1 | находим определитель матрицы (маленький треугольник )=4*(11*1-2*(-10))-2*(4*1-2*(-2))+0*(4*(-10)-11*(-2))=108Помогите с заданием решившему два или три задания дам лучшее решение.
1) Найти координаты X если Х перпендикулярен i-2j+k, x перпендикулярен 2i-3j+k, а модуль вектора Х равен 6*(корень из 3)
2) Проверить принадлежат ли точки А(-1;3;4) B(0;1;5) C(-2;3;5) D(6;0;0) одной плоскости, составить уравнение плоскости.
3) Составить уравнение прямой через точку А(1;3;2) паралельно плоскости XOY и образует угол 45 с прямой X/1=y/1=z/0. Сколько ответов имеет задача?
Решение: Делаем из четырёх точек три вектора (одну соединяем с тремя остальными), находим координаты этих векторов, вычитая координаты начала вектора из координат конца вектора, далее находим смешанное произведение этих векторов (численно равно определителю, строки которого и есть эти вектора в любом порядке). Если смешанное произведение равно нулю, значит эти вектора (а значит и эти точки) лежат в одной плоскости, если не равно нулю-то не лежат. Это универсальный стандартный способ. это к номеру 2 Для номера 1. Для перпендикулярности двух ненулевых векторов необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, учитывая данное условие состаляем уравнения Х(x,y,z) -обозначим так коорд. Х x-2y+z=0 2x-3y+z=0 Третье уравнение получаем из формулы модуля: х^2+y^2+z^2=108
Найти неизвестную координату вектора а=xi+3j-3k, если модуль а =5
Решение: Для вектора $$ a= { a_x;a_y;a_z }$$
модуль равен
$$ |a|=\sqrt{a^2_x+a^2_y+a^2_z} $$
отсюда используя условие получим
$$ a_x=x;a_y=3;a_z=-3 \\ 5=\sqrt{x^2+3^2+(-3)^2} \\ 25=x^2+9+9 \\ x^2=25-18 \\ x^2=7 $$
откуда неизвестная координата х равна $$ -\sqrt{7} $$ или $$ \sqrt{7} $$
В вариантах 1–10 даны координаты точек А, В, С. Требуется: а) записать векторы и и найти модули этих векторов; б) найти угол между векторами и ;
Решение: a) |A|=√(0^2+(-3)^2+3^2)=√(9+9)=√18
|B|=√(5^2+(-2)^2+3^2)=√(25+4+9)=√38
|C|=√(3^2+2^2+7^2)=√(9+4+49)=√62
б) сначала находим скалярное произведение векторов:
ABC=0*5*3+(-3)(-2)2+3*3*7=12+63=75
далее надо найти длину (т. е. модуль), которая нам уже известна (сма)
после необходимо перемножить эти длины и получаем:
√18*√38*√62=√9*2*9.5*4*15.5*4=3*2*2√9.5*15.5*2=12√294.5
(дурацкие какие-то значения получаются)
и наконец, делим скалярное произведение векторов на произведение длин этих векторов, получаем:
75/12√294.5=25\4√294.5 -это cos
сам угол равен arccos(25\4√294.5)Найдите координаты вектора b коллинеарного вектору a{-3;2}, если a*b=39
Решение: $$ a=(-3,2),\; \; b=(x,y)\\\\a\cdot b=-3x+2y=39\\\\\overline{a}||\overline{b}\; \; \to \; \; \frac{-3}{x}=\frac{2}{y}\; \; \to \; \; -3y=2x\\\\ \left \{ {{-3x+2y=39} \atop {-3y=2x}} \right. \; \left \{ {{-3x+2\cdot \frac{2x}{-3}=39} \atop {y=\frac{2x}{-3}}} \right. \\\\-3x-\frac{4x}{3}=39,\; \; \frac{-13x}{3}=39,\; \; x=-9,\; \; y=\frac{-18}{-3}=6\\\\\overline{b}=(-9,6) $$|a|=√13
a{-3; 2}
b{-3x; 2x}
|b|=√13|x|
если векторы коллинеарны, то ab = +- |a|*|b|
39= + - 13 |x|
|x|= + - 3
b{-9; 6} или b{9; -6}Найдите координаты вектора b коллинеарного вектору a(2корня из 2; -1;4) если |b|=10
Решение: a(2√2 ;- 1 ; 4) ;
Координаты коллинеарных векторов пропорциональны :
b(2√2k ; -k ; 4k).
модуль(длина) вектора b :
|b| =√(2√2k)²+( -k)² +(4k)²) ;
10 = 5|k| ;
k = ±2.
ответ : b(-4√2 ;2 ; - 8) или b (4√2 ; -2 ; 8).
Найдите координаты векторов a+b и a-b если a {-8;16}и b{13;-6}
Решение: Имеете a(-2;3;6), b(0;6;-8)
складывая векторы ты попарно складываете соответствующие координаты векторов
потому имеем (a+b) = (-2+0; 3+6; 6 +(-8))=(-2; 9; -2). т. е. получили новый вектор.
скалярное умножение векторов суть сумма попарно перемноженных соответствующих координат векторов и потому имеем
b(a+b) = (0;6;-8) (-2; 9; -2) = 0*(-2) + 6*9 + (-8)*(-2)=70Найдите координаты и длину вектор а=-b+1/2 вектор с
Вектор b {3;-2}
Вектор с{-6;2}
Решение: -b - это вектор, противоположный вектору b, поэтому его координаты противоположны координатам вектора b, это будет (-3;2)
1/2с = 1/2(-6; 2) = (-3;1). Использовали правило умножения вектора на число: чтобы умножить вектор на число, надо каждую координату вектора умножить на это число.
Теперь выполняем сложение и получаем
а = (-3; 2) + (-3; 1) = ( -6; 3)
Если всё это записать кратко, то будет так:
а = -(3; -2) + 1/2(-6; 2) = (-3; 2) + (-3; 1) = ( -6; 3)
Длина вектора равна: корень квадратный из суммы квадратов его координат.
(-6)^2 + 3^2 = 36 + 9 = 45
IaI (это длина вектора а)= корень из 45 = 3 на корень из 5
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...