координаты »

найдите координаты середины

  • 1) Дан треугольник ABC с вершинами А (11;-2;-9), В (2;6;-4) С (8;-6;-8)
    а) Найдите координаты середины отрезка ВС
    б) Найдите координаты и длины вектора ВС
    в) Найдите вектор АВ + ВС
    г) Докажите перпендикулярность векторов АВ и АС
    2) Даны вершины треугольника А (1 3 0) В (1 0 4) С (-2 1 6) Найти косинус угла А этого треугольника
    3) Даны три вершины параллелограмма АВСД А (0 2 -3) В (-1 1 1) С (2 -2 -1) Найдите координаты четвертой вершины Д


    Решение: 1) Дан треугольник ABC с вершинами А (11;-2;-9), В (2;6;-4) С (8;-6;-8) а) ВСser = ((2+8)/2, (6+-6)/2, (-4+-8)/2) = ( 5, 0,6 )
    б) Найдите координаты и длины вектора ВС
    $$ [BC]= \sqrt{(8-2)^{2} + (-6-6)^{2} + (-8-4)^{2}} = \sqrt{ 6^{2} + 12^{2} +(-12)^{2}} = \\ \sqrt{36+144+144} = \sqrt{324} = 18 $$
    в) Найдите вектор АВ + ВС
    Тут просто два вектора нарисовать, причем второй вектор начинается в точке Б. Затем соединить вершины А и С.
    г) Докажите перпендикулярность векторов АВ и АС
    Рисовать, иначе не увидите. Можно вычислить косинус, если равен нулю - значит перпендикулярны. Но это вряд ли математика 5-го класса.
    2) Даны вершины треугольника А (1 3 0) В (1 0 4) С (-2 1 6) Найти косинус угла А этого треугольника
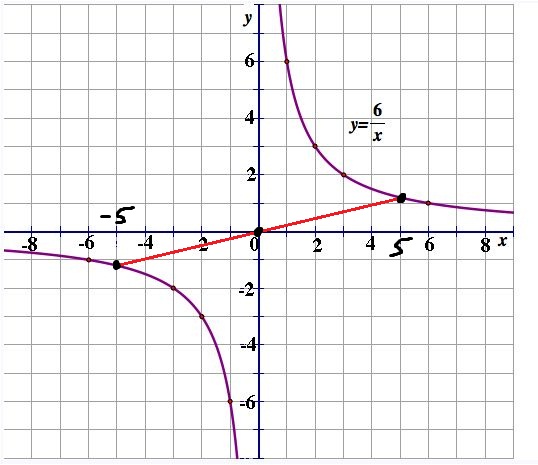
    3) Даны три вершины параллелограмма АВСД А (0 2 -3) В (-1 1 1) С (2 -2 -1) Найдите координаты четвертой вершины Д

  • Постройте график функции y= 6/x. Найдите координаты середины отрезка, соединяющего точки этого графика с абсциссами 5 и -5


    Решение: Отметим на полученном графике точки с абсциссами 5 и –5 и соединим их отрезком. Координаты середины этого отрезка (0; 0)

    ======================

    см. рис

    Отметим на полученном графике точки с абсциссами и и соединим их отрезком. Координаты середины этого отрезка см. рис...

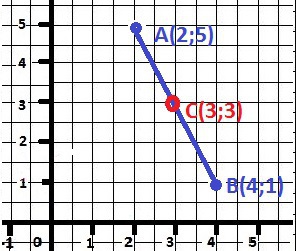
  • 1) Найдите координаты середины отрезка AB
    a)(2;5), B(4;1)
    b) A(-2;3), B(6;-1)
    2) Найдите координаты точки B, если точка М является координатой середины отрезка АВ. a)(2; 1), M(3; 2) b) A(3; -1), M(-1; 1)
    3) Найдите координаты середин сторон треугольника с вершинами
    A(0; 0), B(0; 4) и C(-6; 0)
    4) a) Точки А(2;3) и C(4; 1) являются противоположными вершинами параллелограмма АВСD. Найдите координаты точки пересечения диагоналей параллелограмма.
    b) Точки А(1; 3), B(2; 6) и C(5; 7) вершины параллелограмма ABCD. Найдите координаты вершины D


    Решение: 1)
     Сх = (Ах+Вх)/2 = (2+4)/2 = 3
    Су=(Ау+Ву)/2 = (1+5)/2 = 3
    С(3;3) - ОТВЕТ
    2) Симметрия - расстояния от точки М до точки С равны.
    Сх= Ах + 2*(Мх-Ах) = 2+2(3-2) = 4
    Су= Ау+2*(Му-Ау) = 1+2-(3-2) = 3 
    С(4;3) - ОТВЕТ
    4а) - середина отрезка - полусумма координат.
    Ох =(Ах+Сх)/2 = (2+4)/2 = 3
    Оу=(Ау+Су)/2 = (1+3)/2= 2
    О(3;2) - ОТВЕТ
    4б) Параллелограмм - АВ║CD и AD║BC. Параллельно - значит наклоны одинаковы, значит и разности координат равны.
    Cx-Bx = 5-2 = 3 и Cy-By= 7-6 = 1 - нашли разности координат.
    Теперь прибавили к координатам точки А.
    Dx= Ax+3 = 1+3 =4
    Dy=Ay+1 = 3+1 = 4
    D(4;4) - ОТВЕТ 

     Сх Ах Вх Су Ау Ву С - ОТВЕТ Симметрия - расстояния от точки М до точки С равны.Сх Ах Мх-Ах - Су Ау Му-Ау - -  С - ОТВЕТ а - середина отрезка - полусумма координат.Ох Ах Сх О...

  • даны точки А(-1;4;3) и В(5;-2;-0) а) Найдите координаты середину АВ б) Точка B - середина отрезка АС. в) найдите длину отрезка ав


    Решение: Пусть T - середина АВ
    $$ T( \frac{-1+5}{2} ; \frac{4-2}{2} ; \frac{3+0}{2} )=(2;1;1,5) \\ $$
    Так как В - середина отрезка АС, пусть координаты С будут $$ (x;y;z) $$.
    Найдем их через точку В, которая есть серединой АС:
    $$ 5= \frac{-1+x}{2}\stackrel{.}{\Longrightarrow}-1+x=10\stackrel{.}{\Longrightarrow}x=11 \\ -2=\frac{4+y}{2}\stackrel{.}{\Longrightarrow}4+y=-4\stackrel{.}{\Longrightarrow}y=-8 \\ 0= \frac{3+z}{2}\stackrel{.}{\Longrightarrow}3+z=0\stackrel{.}{\Longrightarrow}z=-3 \\ C(11;-8;-3) $$
    Длина отрезка АВ:
    $$ AB= \sqrt{(5+1)^2+(-2-4)^2+(0-3)^2}= \sqrt{36+36+9} = \sqrt{81}=9 $$Пусть T - середина АВ T frac - frac - frac Так как В - середина отрезка АС пусть координаты С будут  x y z .Найдем их через точку В которая есть серединой АС frac - x stackre...

  • Даны точки B(-1;4) М(2;-3) F(1;-3) и K(4;4)
    1) Разложите вектор MK по координатам вектора i и j
    2) Найдите координаты середины отрезка FM
    3) Напишите уравнение окружности с центром в точке K, радиуса KB


    Решение: 1) MK={4-2;4-(-3)}={2;7}
    MK=2i+7j
    2)
    предположим, точка О-середина отрезка
    xo=(xf+xm)/2=(1+2)/2=1.5
    yo=(yf+ym)/2=(-3+(-3))/2= -3
    координаты середины отрезка FM (1.5;-3)
    3) центр К(4;4)
    радиус КВ
    определим вектор КВ по точкам
    КВ={-1-4;4-4}={-5;0}
    найдем длину радиуса КВ
    /КВ/=V(-5)^2+0^2)=V25=5
    уравнение окружности
    (x-x0)^2+(y-y0)^2=R^2
    (x-4)^2+(y-4)^2=25
    V- это знак корня

  • Даны точки А(5,2,1) и В(-3,4,7)
    а) найдите координаты середины отрезка АВ
    б) найдите координаты точки С, если точка А-середина отрезка СВ
    2
    Даны векторы а(2,6,3) и б(-1,2,2)
    Найдите |а+b|
    |a|+|b|
    3) даны точки А(2,1,8) В (1,5,0)
    С(8,1,4)
    А) докажите что треугольник авс равнобедренный
    Б) найдите длину средней линии треугольника соединяющей середины боковых сторон


    Решение: 1
    a) М-середина
    х=(5-3)/2=1  y=(-2+4)/2=1  z=(1+7)/2=4
    M(1;1;4)
    b)5=(x-3)/2⇒x-3=10⇒x=13
    -2=(y+4)/2⇒y+4=-4⇒y=-8
    1=(z+7)/2⇒z+7=2⇒z=-5
    C(13;-8;-5)
    2
    a+b={1;-4;1}
    |a+b|=√1+16+1=√18=3√2
    |a|+|b|=√4+36+9+√1+4+4=√49+√9=7+3=10
    3
    AB=√(1-2)²+(-5-1)²+(0+8)²=√1+36+64=√101
    BC=√(8-1)²+(1+5)²+(-4-0)²=√49+36+16=√101
    AC=√(8-2)²+(1-1)²+(-4+8)²=√36+0+16=√52=2√13
    AB=BC- треугольник равнобедренный
    Средняя линия равна 1/2АС=1/2*2√13=√13

  • Найдите координаты середины отрезка AB, если A (-2;3) а B (4;5)


    Решение: по теореме о координатах середины отрезка. каждая координата середины отрезка равна полусумме одноименных координат этого отрезка

  • 1) Найдите координаты середины отрезка АС, если : А(2;-7;-6),C(6;-3;-2)
    2) Найдите расстояние между точками М и К, если :
    М(9;-3;-6), К (1;5;-10)


    Решение: 1) для начала найдем координаты отрезка АС, для этого от координат конца отнимаем координаты начала и получаем: АС(4;4;4;), затем делим на 2 и получаем координаты середины вектора (2;2;2)
    Ответ:(2;2;2)
    2) для начала найдем координаты отрезка МК, для этого от координат конца отнимаем координаты начала и получаем: МК(-8;8;4), затем находим длину МК=корень из 64+64+16=12
    Ответ:12 см расстояние

  • Отметьте на координатной плоскости точки М(0;-4) и N(6;2) и соедините из отрезкой. Найдите координаты середины отрезка МN


    Решение: Координаты пересечения с осью х (4,0) 
    Середина отрезка вычисляется по теореме Пифагора, т. к. он является гипотенузой прямоугольного треугольника, координаты углов которого (0,4);(0,2) и (6,2), катеты равны 6 и 6. 6²+6²=с²
    с=√72≈8.485. Середина отрезка - 8.485:2≈4.24

  • Постройте в координатной плоскости треугольник MKN если M-7;-5 N-3;5 K7;1 измерьте углы и стороны этого треугольника найдите координаты середины стороны MN рисунок )


    Решение: |MN|²=(-3-(-7))²+(5-(-5))²=4+10=116
    |MK|²=(7-(-7))²+(1-(-5))²=14+6=232
    |NK|²=(7-(-3))²+(1-5)²=100+16=116
    |MN|=|NK|
    видим
    232=116+116
    |MK|²= |MN|²+ |NK|²
    отсюда следует, что треугольник прямоугольный и равносторонний
    значит углы 45,45 и 90 градусов
    |MN|=√116=2√29
    |MK|=√232=2√58
    |NK|=√116=2√29
    P точка пересечения МК с осью оY
    |PK|²=7²+3²=58
    |PM|²=7²+3²=58
    |MN|²=116=58+58
    точка Р делит МК пополам с координатами (0;2)

1 2 > >>