координаты »

найдите координаты вершины параболы

  • Найдите вершину, ось и точки пересечения с осями координат параболы и постройте ее график y=x^2-2x-8


    Решение: У=х²-2х-8
    Вершина : х₀=2:2=1; у₀=1-2-8=-9
    Точка пересечения о осьюОУ имеет координаты (0;-8)
    Точки пересечения с осью ОХ имеют координаты (4;0);(-2;0)
    х²-2х-8=0
    D=4+32=36; x₁=4; x₂=-2
    Рисунок

    У х - х- Вершина х у - - - Точка пересечения о осьюОУ имеет координаты - Точки пересечения с осью ОХ имеют координаты - х - х- D x x - Рисунок...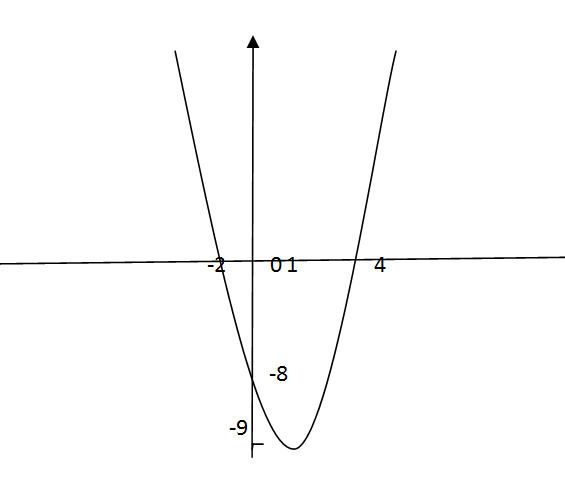

  • Найдите вершину, ось и точки пересечения с осями координат параболы и постройте ее график y=x^2-4x+3


    Решение: Существуют формулы нахождения вершины параболы m(x)= -b/2a это значение x также имеется у можно найти просто подставив значение у график
    m(x)= -4/2×1=-2
    n(y)=(-2)^2-4×(-2)+3= 4+8+3=15
    чтобы найти точки пересечения приравниваем функцию нулю
    находим дискриминант x1 и
    x^2-4x+3=0
    Д= b^2-4×ac=16-12=4 √4=2
    x1=(-b-√Д)/2а= 1
    x2=(-b+√Д)/2а=3
    точки пе рё сечения графика с осью ох 1;3
    вершина параболы (-2;15)

  • 1. Для квадратичной функции у=2х^2+7х-3 найти у(-3)
    2, Дана функция у=5/х-1+2 Найдите у(6)
    3. Найдите координаты вершины параболы у=-3(х-2)^2-4
    4. Напишите уравнение оси симметрии параболы у=х^2+4x-5
    5. Запишите уравнение параболы у=х^2+рх+q, вершина которой находится в точке А(-3;-4)
    6. Постройте график функции у=(х+1)^2-2


    Решение: 1)y=2x^2+7x-3
    y(-3)=2*(-3)^2-7*3-3=18-21-3= -6
    2y=5/(x-1)+2
    y(6)=5/(6-1)+2=7
    3)y= -3(x-2)^2-4=-3(x^2-4x+4)-4= -3x^2+12x-12-4= -3x^2+12x-16
    x0= -b/2a
    b=12
    a= -3
    x0= -(12/(2*(-3))=2
    y(2)= -3*4+24-16= -4
    вершина  (2;-4)
    4)y=x^2+4x-5
    x0=-b/2a
    x0= -4/2= -2
    ось симметрии прямая х= -2
    5)y=x^2+px+q
    A(-3;4)
    х0= -3
    x0=-b/2a
    -3=-p/2
    -p=(-3)*2=-6
    p=6
    y(-3)=-4
    (-3)^2+6*(-3)+q=-4
    9-18+q= -4
    q=5
    y=x^2+6x+5
    6) на фото

    1)y=2x^2+7x-3
    y(-3)=2*(-3)^2-7*3-3=18-21-3= -6
    2y=5/(x-1)+2
    y(6)=5/(6-1)+2=7
    3)y= -3(x-2)^2-4=-3(x^2-4x+4)-4= -3x^2+12x-12-4= -3x^2+12x-16
    x0= -b/2a
    b=12
    a= -3
    x0= -(12/(2*(-3))=2
    y(2)= -3*4+24-16= -4
    вершина  (2;-4)
    4)y=x^2+4x-5
    x0=-b/2a
    x0= -4/2= -2
    ось симметрии прямая х= -2
    5)y=x^2+px+q
    A(-3;4)
    х0= -3
    x0=-b/2a
    -3=-p/2
    -p=(-3)*2=-6
    p=6
    y(-3)=-4
    (-3)^2+6*(-3)+q=-4
    9-18+q= -4
    q=5
    y=x^2+6x+5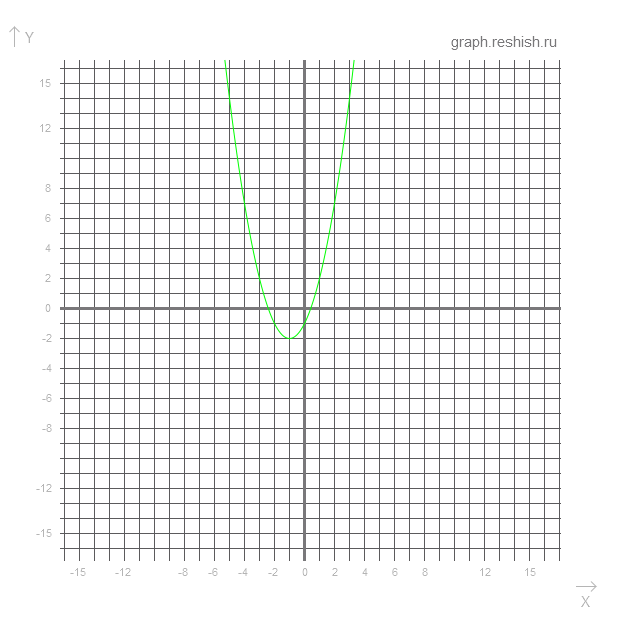

    y x x- y - - - - - - - y x- y - y - x- - - x - x - - x x- - - x x- x -b ab a - x - - y - - - вершина  - y x x- x -b ax - - ось симметрии прямая х - y x px qA - х - x -b a- -p...

  • Найдите вершину параболы, ось симметрии и точки пересечения с осями координат. Постройте график. y=-x^2+2x


    Решение: точки пересечения с осями координат находятся из условия равенства 0.

    пересечение с осью ОХ - у=0

    -x^2+2x = 0

    x^2 - 2x = 0

    x(x-2) = 0

    x = 0 или х = 2

    пересечение с осью ОУ - х=0

    у = -0+0 = 0

    ось симметрии имеет уравнение: х = -b/(2a) (это часть формулы для корней уравнения.)

    х = 2/2 = 1

    вершина параболы лежит на ее оси => координата х уже известна х=1

    осталось найти у

    у = -1^2 + 2*1 = -1+2 = 1

    координаты вершины (1; 1)

    график -парабола, ветви вниз.

  • 1. Найдите значение функции у=х (в квадрате)+2х-7 при х=3
    2. Найдите нули функции у=х(в квадрате)+5х
    3. Найдите координаты точки пересечения графика функции у=х(в квадрате)+6х-9 с осью Оу.
    4. Найдите координаты вершины параболы у=-3х(в квадрате)+12х+5 (все делается без чертежа)


    Решение: 1. Найдите значение функции у=х (в квадрате)+2х-7 при х=3

      y=3 (в квадрате) +2*3-7=9+6-7=8
    2. найдите нули функции у=х(в квадрате)+5х

      х(в квадрате)+5х =0

      x(x+5)=0

      x=0 или х+5=0

      Нули функции: 0 и -5
    3. Найдите координаты точки пересечения графика функции у=х(в квадрате)+6х-9 с осью Оу.
    Точка, лежащая на оси Оу, имеет координаты: х =0 и какой-то у, т. (0; у)

    Подставим в уравнение функции х=0 и найдем у:

    у= 0 (в квадрате) =6*0-9 = -9
    4. Найдите координаты вершины параболы у=-3х(в квадрате)+12х+5

     х(вершины)= -b/(2*a), если квадратичная функция задана формулой y=a*x (в квадрате)+b*x+c

     х(вершины)=-12/(2*(-3))=-12/(-6)=  2

    y(вершины)= -3*2 (в квадрате)+12*2+5=-3*4+24+5=-12+29=17

    Т. о. вершина имеет уоординаты (2; 17)

    1. y(3)=3²+2*3-7=8.

    2. y=x²+5x=x(x+5); x₀=0; x₀=-5.

    3. y(0)=0²+6*0-9=-9.

    4. y=-3x²+12x+5;

    x₀=-b/2a=-12/-6=2; y₀=y(2)=-12+24+5=12+5=17.

    A(2;17) - вершина.

  • Найдите координаты вершины параболы:
    а) f(x)=x^2-6x+4;
    б) f(x)=-x^2-4x+1
    в)f(x)=3x^2-12x+2;
    При вычислении воспользуйтесь формулами
    m=-b/2a и n=f(-b/2a), где m и n координаты вершины параболы f(x) =ax^2+bx+c


    Решение: Найдите координаты вершины параболы:
    а) f(x)=x²-6x+4;
    б) f(x)=-x²-4x+1
    в)f(x)=3x²-12x+2;
    При вычислении воспользуйтесь формулами 
    m=-b/2a и n=f(-b/2a), где m и n координаты вершины параболы f(x) =ax^2+bx+c
    Решение:
    а) f(x)=x²-6x+4;
    В приведенном уравнение b =-6, a=1
    m=x=-b/2a =-(-6)/(2*1)=6/2=3
    n=y(3)=3²-6*3+4=9-18+4=-5
    Вершина параболы y= x² - 6x + 4 находится в точке с координатами m=х=3, n=у(3)=-5
    б) f(x)=-x²-4x+1
    В приведенном уравнение b =-4, a=-1
    m=x=-b/2a =-(-4)/(2*(-1))=-4/2=-2
    n=y(-2)=-(-2)²-4*(-2)+1=-4+8+1= 5
    Вершина параболы y= -x² - 4x + 1 находится в точке с координатами m=х=-2, n=у(-2)= 5
    в)f(x)=3x²-12x+2
    В приведенном уравнение b =-12, a=3
    m=x=-b/2a =-(-12)/(2*3)=12/6= 2
    n=y(2)=3*2²-12*2+2=12-24+2= -10
    Вершина параболы y= 3x²-12x+2 находится в точке с координатами m=х=2, n=у(2)= -10

  • 1) Найдите координаты m пересечения параболы y=2x2-7x+8;y2=5x-2x2 2) Найдите множество решений неравенства 5х,3/4 - 3-х/5>2-х/10


    Решение:

  • №1) Найдите f(-5), если f(x) =-x^2-7x+11
    №2) Найдите координаты вершины параболы y=x^2-8x-3
    №3) Найдите множество значений функции y=x^2+3 на отрезке [-2:4]


    Решение: 1)
    $$ f(x)=-x^2-7x+11\\f(-5)=-(-5)^2-7*(-5)+11=-25+35+11=21 $$
    2)
    Координаты вершины параболы y=ax²+bx+c вычисляются по формулам:
    $$ x_v=-\frac{b}{2a}\\y_v=ax_v^2+bx_v+c $$
    Воспользуемся:
    $$ x_v=-\frac{-8}{2*1}=\frac{8}{2}=4\\y_v=4^2-8*4-3=-19\\A_v(4;-19) $$
    3)
    Находим наименьшее и наибольшее значений функции на этом отрезке.
    Для начала находим производную.
    $$ y=x^2+3\\y’=2x $$
    Далее находим нули производной:
    $$ y’=0\\2x=0\\x=0 $$
    x=0 - критическая точка(может быть максимумом или минимумом функции).
    Наносим критические точки на координатную прямую, находим знаки производной на интервалах. Там где производная положительная функция возрастает, отрицательная - убывает.

    Находим значения функции на концах отрезка и в точке минимума:
    y(-2)=(-2)²+3=4+3=7
    y(4)=4²+3=16+3=19
    y(0)=0²+3=3
    Значит множество значений функции y∈[3;19]

  • 1) Найдите коородинаты вершины параболы и определите направление ветви:
    y=-x^2-8x+3
    2) Найдите наименьшее значение функции:
    y=x^2-x-10


    Решение: Помогите, пожалуйста:

    1) Найдите коородинаты вершины параболы и определите направление ветви:

    y=-x^2-8x+3

    2) Найдите наименьшее значение функции:

    y=x^2-x-10 

    1) Найдите коородинаты вершины параболы и определите направление ветви:

    y=-x^2-8x+3

    xo=-b/2a=8/-2=-4 yo=f(-4)=-16+32+3=19 (-4,19)

    2) Найдите наименьшее значение функции:

    y=x^2-x-10 

    minf(x)=yo=-D/4a=-(1+40)/4=-10 1/4

  • Найдите координаты вершины параболы и определите направление ветви:
    1) у=х (в квадрате) -4х+3
    2) у=-х(в квадрате) -12х+1
    3) у= х( в квадрате) -10х +15
    4) у=-х(в квдрате) -8х+3


    Решение: всё написано с: 

    1) ветви вверх, координаты вершины xo=4/2=2,y0=2^2-4*2+3= -1 ( 2;-1)
    2) ветви вниз, x0=12/2=6 y0=-6^2-12*6+1= -83 ( 6;-83)
    3) ветви вверх x0= 10/5=2 y0=4-10*2+15=-1 (2;-1)
    4) ветви вниз x0= 8/2=4 y0= -4^2-8*(-4)+15= -8+32+15=39 (4;39)

1 2 > >>