координаты »

множество точек на координатной плоскости

  • Какое множество точек задаёт на координатной прямой плоскости неравенство 1) (x-1)(y-1)>=0; 2) x^2-y^2>0 ?

    (больше или равно)


    Решение: Если эти неравенства не связаны, то то, что во вложении.

    (для первого неравенства "прямой крест", для второго "косой")

    Если эти неравенства не связаны то то что во вложении. для первого неравенства прямой крест для второго косой...

  • Построить множество точек на координатной плоскости OXY с координатами (х,у) удовлетворяющими условию х*/у/=х^2


    Решение: 1. Нарисуй систему координат ХУ и нанеси на координатные оси разметку 
    2. Проведи две параллельные прямые на расстоянии 0,5 от оси ОХ, одну выше, другую ниже. 
    3. Заштрихуй область выше верхней прямой и ниже нижней. 
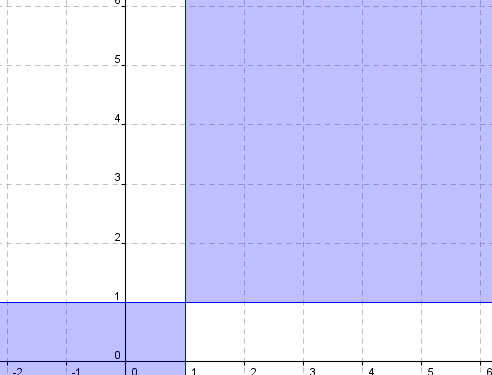
    Это и будет искомое множество точек.

  • 1) Выделив штриховкой множество точек координатной плоскости, координаты которых удовлетворяют системе условий x>=-1 и y=<4 укажите наибольший радиус окружности (x-5)^2+(y-1)^2=R^2, все точки которой принадлежат данному множеству? 2) Найти значение выражения \( \sqrt[10]{{(5-3x})^{10}} - |3x+4| \), если x∈[2;3]


    Решение: 1) Чертите оси Х и У.Из т.4 на оси У проводите пунктиром прямую, параллельно оси ОХ. Из т. -1 на оси Х проводите пунктиром прямую параллельно оси ОУ. Заштриховываете область ниже первой прямой, но правее - второй.

    Находите точку с координатами (5; 1). Это и есть центр окружности. Тихонечко проводите окружность с радиусом R = 3 - это и есть наибольший возможный радиус окружности, еще попадающей в заштрихованную область.

    2)  = (3х-5) -(3х+4), так как (5-3х)мен 0 на указанном промежутке, а (3х+4)бол0 на этом промежутке.

     (3х-5) -(3х+4) = -9.

    Ответ: -9.

    Чертите оси Х и У.Из т. на оси У проводите пунктиром прямую параллельно оси ОХ. Из т. - на оси Х проводите пунктиром прямую параллельно оси ОУ. Заштриховываете область ниже п...

  • Найдите множество точек координатной плоскости: 1) модуль которых равен 2; 2) аргумент которых равен \( \frac{3\pi}{4} \).


    Решение: 1) Модуль - это расстояние от начала координат О(0; 0) до точки.
    Точки, модуль которых равен 2 - это окружность с центром О(0,0) и R = 2.
    2) Соедини точку отрезком с началом координат О(0; 0).
    Аргумент точки - это угол наклона этого отрезка к оси Ох.
    Точки, аргумент которых равен такому-то углу - это луч под таким углом.
    Для твоего угла 3pi/4 - это диагональ 2 четверти из начала координат.

  • Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условиям \(\begin{cases}2|x|+|y-1|\geq2\\x^2+y^2-2y\leq3\end{cases}\) и найдите площадь получившейся фигуры.


    Решение: S=S(круга)-S(ромба)=πR²-(1/2)·d₁·d₂=π·2²-(1/2)·4·2=4π-4 кв. ед.
    х²+y²-2y≤3  ⇒ x²+(y-1)²≤4-  внутренняя часть круга радиуса R=2 с центром в точке (0;1).
    2|x|+|y-1|≥1
    Раскрываем модуль:
    1) х≥0; у-1 ≥0  получаем 2х+у-1≥2  или   у≥-2х+3  часть плоскости ограниченная тремя неравенствами х≥0; у≥1; у≥-2х+3  ( см. рис. 2) красного цвета
    2) х<0; y-1<0  получаем неравенство -2x-y+1≥2  или у ≤-2х-1
     Часть плоскости, ограниченная тремя неравенствами х<0; у<1; у≤-2х-1  ( см. рис. 2) желтого  цвета
    и аналогично
    3) x≥0; y-1<0  получаем неравенство  2х-у+1≥2   или   у≤2х-1
    Часть плоскости, ограниченная неравенствами х≥0; у< 1; y ≤2х-1
    4) x<0; y-1≥0 получаем неравенство -2х+у-1≥2  или  у≥2х+3.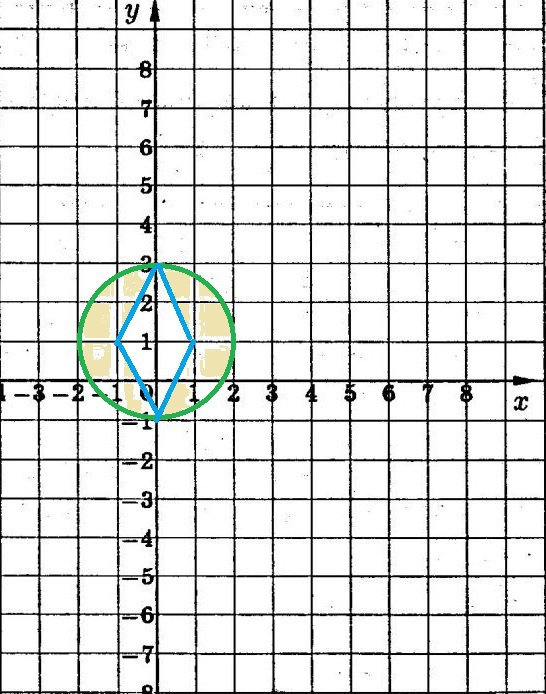

    S S круга -S ромба R - d d - - кв. ед.х y - y   x y- -  внутренняя часть круга радиуса R с центром в точке . x y- Раскрываем модуль х у-   получаем х у-   или   у - х   часть...

  • Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условиям
    Далее система
    2|x|+|y -1|≥2
    x^2+y^2 -2y≤3
    и найдите площадь получившейся фигуры.


    Решение:
     $$ 2|x|+|y-1| \geq 2\\ x^2+y^2-2y \leq 3 \\ \\ x^2+y^2-2y+1 \leq 2^2 \\ x^2+(y-1)^2 \leq 2 ^2 $$ 
      То есть это окружность с центром $$ (1; 0 )\\ R=2 $$ 
      На отрезке $$ x \in (-2;-1]\\\\ $$
      Очевидно что $$ \sqrt{(y-1)^2} \geq 0\\ $$, значит   $$ 1- \sqrt{4-x^2} \leq y \leq \sqrt{4-x^2 }+1 $$ 
     На отрезке $$ x \in (-1;0)\\\\ -2x+|y-1| \geq 2 \\ |y+1| \geq 2x+2 \\ y \geq 3+2x\\ y \leq -1-2x $$
     И так далее, получим
     Получим 6 отрезков, включая две полуокружности задаваемой
      $$ 1-\sqrt{4-x^2} \leq y \leq 1+\sqrt{4-x^2} $$ 
     на отрезке $$ -2\ < \ x \leq -1\\ 1 \leq \ < \ x\ < \ 2 $$ 
     То есть получим ромб, который не будет включен в решение, со сторонами 
      $$ \sqrt{2^2+1^2}=\sqrt{5} $$ 
      $$ cos\alpha = \frac{3}{5}\\ sin\alpha = \frac{4}{5}\\ 2S_{romb} = \frac{2*\frac{4}{5}}{2}*5 = 4\\ S_{rew}=4\pi-4=4(\pi-1) $$

  • 1) Выделив штриховкой множество точек координатной плоскости, координаты которых удовлетворяют системе условий x>=-1 и y=<4 укажите наибольший радиус окружности (x-5)^2+(y-1)^2=R^2, все точки которой принадлежат данному множеству?
    2) Найти значение выражения \( \sqrt[10]{{(5-3x})^{10}}-I3x+4I \), если x∈[2;3]


    Решение: 1) Чертите оси Х и У. Из т.4 на оси У проводите пунктиром прямую, параллельно оси ОХ. Из т.1 на оси Х проводите пунктиром прямую параллельно оси ОУ. Заштриховываете область ниже первой прямой, но правее - второй.

    Находите точку с координатами (5; 1). Это и есть центр окружности. Тихонечко проводите окружность с радиусом R = 3 - это и есть наибольший возможный радиус окружности, еще попадающей в заштрихованную область.

    2)  = (3х-5) -(3х+4), так как (5-3х) мен 0 на указанном промежутке, а (3х+4) бол0 на этом промежутке.

     (3х-5) -(3х+4) = -9.

    Ответ: -9.