в декартовой системе координат
Найдите площадь прямоугольника, вершины которого заданы координатами в декартовой системе координат А(-2; 0) В(0; -2) С(-3; -5) D(-5 ; -3)
Решение: Решение
Построенный прямоугольник, с данными координатами вершин, в декартовой системе координат образует три прямоугольных треугольника. Для вычисления площади понадобятся два из них
Так как S = a * b, то сторонами прямоугольника являются гипотенузы этих треугольников. Вычислим по теореме Пифагора.
1. AD² = 3² + 3² = 18
AD = √18
2. AB² = 2² + 2² = 8
AB = √8 ⇒
⇒ S = √18 * √8 = √144 = 12 см²
Ответ: площадь прямоугольника равна 12 см²
Найдите площадь прямоугольника, вершины которого заданы координатами в декартовой системе координат А(0; -2), В(1; 0), С(7; -3), D(6; -5).
Решение: Используем формулу для нахождения расстояния между точками.найдем длину АВ, АВ^2=(1-0)^2+(0+2)^2=5,AB=sqrt(5)
BC^2=(7-1)^2+(0+3)^2=36+9=45, BC=sqrt(45)=3*sqrt(5)
S=3*sqrt(5)*sqrt(5)=3*5=15
Есть простая формула S=Q+W/2-1, где Q - количество точек, находящихся внутри фигуры. W - на контуре фигуры. Считать только точки с целыми координатами: (-1;0), (2;3) и так далее.
Постройте в декартовой системе координат точки а(-4;6) и в (8;-3).
Решение: Зто просто на осях Х и У. а(-4,6) это значит х=-4 у=6. Откладываем по оси х в отрицательном направлении 4 единицы, а по оси у поднимаемся вверх с этого места на 6 единиц. Получим точку а. Также в. 8 единиц по оси х. И потом вниз на 3 единицы. За единичный отрезок берем 1 клетку.
^ У
*а ! 6
! 5
! 4
! 3
! 2
! 1
---------- -5- -4-- -3- -2-- -1--0--1--2--3--4---5--6--7--8-> Х
! -1
! -2
! -3 *в
! -4
! -5
! -6
! -7
! -8
как найти координаты точки в декартовой системе координат?
Решение: Данная вам точка имеет координаты. Чтобы их найти, Вы из этой точки опускаете
перпендикуляры на ось Х и ось У и смотрите какие цифры соответствуют Вашей точке.Точка пересечения с осью Х называется абсциссой Вашей точки,а с осью У,
ординатой точки.Координаты записывают (.) А(2,4); (.) С(-3,4) и т.д. На первом месте записывают абсциссу точки, а на втором - ординату. Если точка лежит на оси Х-ов, то ордината ее=0, а если на оси У-ов,,то абсцисса =0. Начало координат - это точка О (0,0), координаты ее = 0.
Найдите площадь квадрата, вершины которого заданы координатами в декартовой системе координат А(-3;0).В(-6;3).С(-3;6).D(0;3).
Решение: Это последовательные вершины квадрата. Найдём расстояние между вершинами, оно будет равно длине стороны квадрата.
$$ AB=\sqrt{(-6+3)^2+(3-0)^2}=\sqrt{9+9}=3\sqrt{2}\\BC=\sqrt{(-3+6)^2+(6-3)^2}=\sqrt{9+9}=3\sqrt{2}\\CD=\sqrt{(0+3)^2+(3-6)^2}=\sqrt{9+9}=3\sqrt{2}\\AD=\sqrt{0+3)^2+(3-0)^2}=3\sqrt{2}\S=3\sqrt{2}\cdot 3\sqrt{2}=9\cdot 2=18 $$
Для того, чтобы найти площадь квадрата, нужно возвести в квадрат длину его стороны.
Найдем сторону, для этого обратимся к рисунку. По рисунку проще всего найти длину стороны AD. Для этого напишем выражение по теореме Пифагора:
AD^2 = 3^2 + 3^2 = 18
Можно было бы найти непосредственно длину отрезка AD, но лучше сразу заметить, что мы нашли как раз то, что искали - сторону в квадрате! Поэтому сразу пишем ответ
S = 18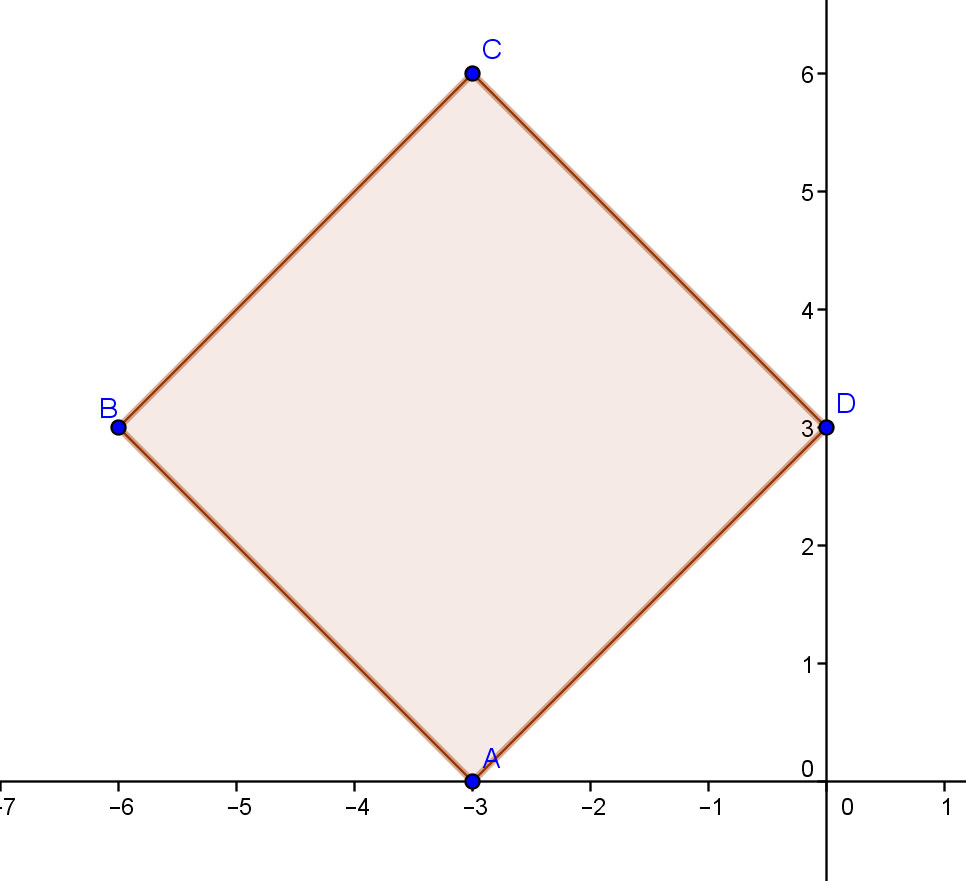
построить вектор с координатами 1,2,3 в декартовой системе координат
Решение: Как я понимаю задание, необходимо сначала найти образ прямой р при центральной симметрии относительно т.М, а затем осуществить параллельный перенос на вектор MN.Возьмем две характерные точки прямой р:
А(0; -3) и В(1; -1). Найдем их образы при центральной симметрии отн.
т. М(-3; 5):
A’: К вектору АМ (-3; 8) прибавляем такой же, получим вектор AA’ (-6;16)
с координатами конца:
х - 0 = -6 х = -6.
у -(-3) = 16 у = 13
Итак A’ (-6; 13).
B’: К вектору ВМ (-4; 6) прибавляем такой же и получим вектор BB’ (-8; 12) с координатами конца:
х - 1 = -8 х = -7
у -(-1) = 12 у = 11.
Итак B’: (-7; 11).
Теперь совершим перемещение точек A’, B’ на вектор MN (4; -4):
Точка A’ (-6; 13) перейдет в точку A" (-2; 9).
Точка B’ (-7; 11) перейдет в точку B" (-3; 7)
Указанные точки принадлежат искомому образу p" данной прямой р. Найдем уравнение этого образа:
у = кх +b
-2k + b = 9, b = 13,
-3k + b = 7, k = 2.
Ответ: у = 2х + 13
Постройте фигуру животного по точкам: (4; -3), (2; -3). (2; -2), (4; -2), (4; -1), (3; 1), (2; 1), (1;2), (0; 0), (-3; 2), (-4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0),(6; 2), (6; -2), (5; -3), (4; -3), (4; -5), (3; -9), (0;-8), (1; -5), (1; -4), (0; -4), (0; -9), (-3; -9), (-3; -3), (-7; -3), (-7, -7), (-8; -7), (-8; -8), (-11; -1), (-14; -3), (-12; -1), (-11; 2), (-8; 4), (-4; 5) Постройте отдельно две точки (2; 4), (6; 4)-это глаза животного ЭТА ЗАДАЧА ПО ТЕМЕ "Декартова система координат на плоскости"
Решение: Животное СЛОН
Рисуем 1 точку (4;-3)
х=4; у=-3
Рисуем 2 точку (2;-3)
х=2; у=-3
Соединяем две точки линией.
Рисуем 3-ью точку (2;-2)
х=2; у=-2
Соединяем точки 2 и 3 линией и т.д.
Декартова система координат:
горизонтальная линия - ось х (справа положительные значения х, слева отрицательные)
вертикальная линия - ось у (вверху положительные значения у, внизу - отрицательные)
Дана точка с координатами x y. Определить номер декартовой системы координат, к которой она принадлежит
Решение: Var x, y: integer;
z: string;
begin
readln(x, y);
if (x > 0) then
if (y > 0) then z := ֵ’
else if (y = 0) then z := ֵ, 4’
else z := ָ’
if (x = 0) then
if (y > 0) then z := ֵ, 2’
else if (y = 0) then z := ִ’
else z := ַ, 4’
if (x < 0) then
if (y > 0) then z := ֶ’
else if (y = 0) then z := ֶ, 3’
else z := ַ’
writeln(’>>’, z, ’<<’);
end.Придумайте задачу на построение фигур по точкам заданным своими координатами по Декартовой системе
Решение: Задача. Построить точки на координатной прямой и соединить их в следующей последовательности:
(1;1)⇒(2;2)⇒(1;3)⇒(2;4)⇒(4;4)⇒(5;3)⇒(4;2)⇒(5;1)⇒(1;1)
фигура изображена на скине внизу
Как найти координаты точки в декартовой системе координат?
Решение: Данная вам точка имеет координаты. Чтобы их найти, Вы из этой точки опускаете перпендикуляры на ось Х и ось У и смотрите какие цифры соответствуют Вашей точке. Точка пересечения с осью Х называется абсциссой Вашей точки, а с осью У,
ординатой точки. Координаты записывают (.) А(2,4); (.) С(-3,4) и т. д. На первом месте записывают абсциссу точки, а на втором ординату. Если точка лежит на оси Х-ов, то ордината ее=0, а если на оси У-ов, то абсцисса =0. Начало координат-это точка О (0,0), координаты ее=0.
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...