координаты »
постройте в системе координат графики - страница 2
Постройте в одной системе координат график функции y=4x+4 и y=-x какая из этих функций является возрастающей?
Решение: Смотрите рисунок, приложенный к ответу. Построим оба графика на одной системе координат. График функции $$ y = -x $$ нарисуем красным цветом, а график функции $$ y = 4x+4 $$ — синим.
Теперь посмотрим, какая из функций возрастает. По графику это определить просто. Нужно посмотреть, «растет» ли график вверх слева направо или «убывает» вниз. Из рисунка видно, что вверх слева направо растет синий график, то есть график функции $$ y = 4x+4 $$.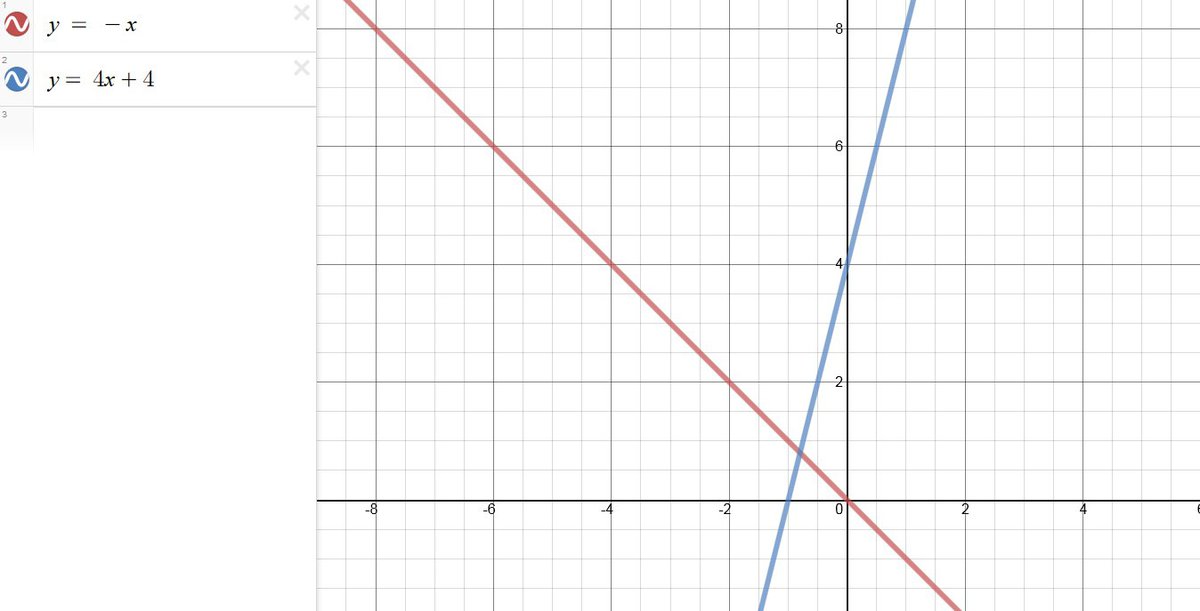
Постройте в одной системе координат графики функций y=-0,5x+2 и y=-2x+5. Найдите координаты точки пересечения графиков функций.
Решение: Я думаю график можно построить
Чтобы найти точки пересечения двух графиков
надо одно значение приравнять к другому
-0,5х+2=-2х+5
1,5х-3=0
1,5х=3
х=2 то есть мы нашли кординаты по х
поставляем любую функцию,чтобы найти у
у= -2*2+5=1
То есть А(2;1) будет точка пересечения
Постройте в одной системе координат графики функций y=-1/3x+1,y=-1/3x-2,y=-1/3x
Решение: Графиком функции является гипербола. В в точке [x = 0], "y" не существует, так как на ноль делить нельзя. "y" наименьшее = - 17/9 ≈ -1.8888888... (8);
вот картинка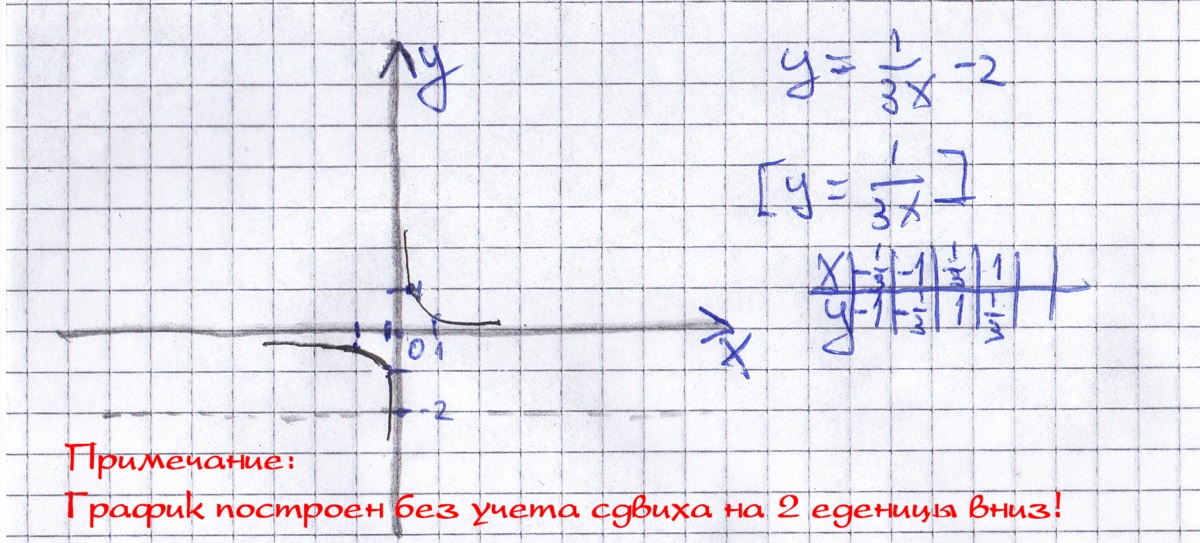
В одной системе координат постройте графики функций y= -0,5x и y=2. Найдите координаты их точки пересечения
Решение:Первая прямая у= -0,5х проходит через начало координат, след
х= 0 4
у= 0 -2
вторая прямая у=2 параллельна оси ОХ и проходит через точки
х= 0 -2
у= 2 2
Строим графики в системе координат по точкам.
По графику смотрим и видим, что точка пересечения А(-4;2).В одной системе координат постройте графики функций y=x y=x+3 y=-x-1
Решение: Первая функция - прямая пропорциональность. Графиком является прямая, проходящая через начало координат.
Две последние функции - линейные, графиками являются прямые.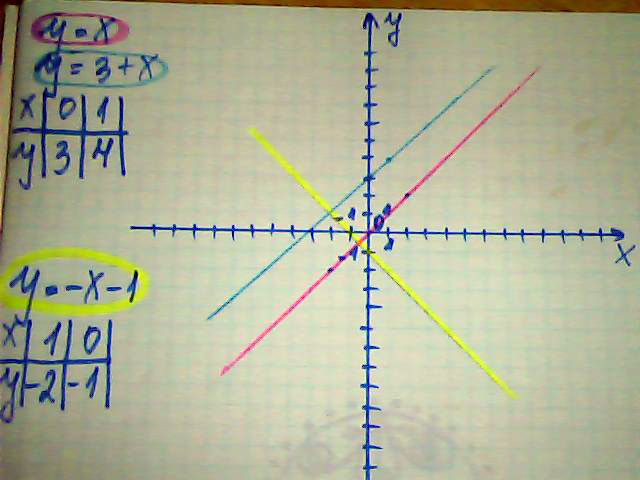
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...