координаты »
система координат x y
В одной системе координат изобразите графики функций: у=log5х, у=log3x
Решение: Y = log₅ x - нижний (синий)
y = log₃ x - верхний (красный)
оба графика проходят через (1; 0)
при x < 0 не существуют
а при х близких к нулю слева стремятся в -∞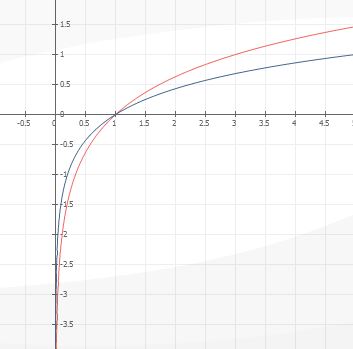
Вычислить площадь области ( с помощью перехода к полярной системе координат) \( x^2 +y^2 \geq e^2, x^2+y^2 \leq e^4 \)
Решение: $$x^2+y^2=e^2 \to r^2cos^2\phi +r^2sin^2\phi=e^2 \\ r^2(cos^2\phi +cos^2\phi )=e^2 \\ r^2=e^2 r=e>0 \\ x^2+y^2=e^4 \to r^2=e^4 \\ r=e^2>0 \\ S=\iint r dr d\phi=4\int_0^{\frac{\pi}{2}}d\phi\int _{e}^{e^2}r\, dr=4\int_0^{\frac{\pi}{2}}(\frac{r^2}{2}_e^{e^2})d\phi =\\=4\cdot \frac{1}{2}\int _0^{\frac{\pi}{2}}(e^4-e^2)d\phi =2(e^4-e^2)\cdot \phi_0^{\frac{\pi}{2}}=\\=2(e^4-e^2)(\frac{\pi}{2}-0)=\pi e^2(e^2-1) $$
Заданная область - кольцо между окружностями с центром в (0,0) и
радиусами $$ r=e, r=e^2. $$Заданы координаты вершин треугольника АВС. Требуется а) построить треугольник в системе координат 0ХУ; б) вычислить его периметр, в) написать уравнения сторон (с проверкой). А(4,4) В(2,2) С(-5,7)
Решение: AB=sqrt(5-2)^2+(3+1)^2=sqrt25=5.. AC=sqrt(5-2)^2+(-2+1)^2=sqrt10. BC=sqrt(5-5)^2+(-2-3)^2=sqrt25=5=>ABC-равнобедр треуг.
cosB=(AB^2+BC^2-AC^2)/ (2*AB*BC(это следует из теор косинусов)=> cosB=(25+25-10) / (2*5*5)= 40 /50=4/5=>уголABC=arccos(4/5)
e)cosB= 4/5=>sinB=sqrt(1-(4/5)^2)=3/5=>уголB=arcsin(3/5)=>S (площ.треуг.) =1/2*AB*BC*sinB=1/2*25*sin(arcsin4/5)=1/2*25*(3/5)=7.5(a) A B = √ ( 3 - 7 ) ² + ( - 3 + 3 ) ² = 4
B C = √ ( 7 - 5 ) ² + ( - 3 - 5 ) ² =2 √ 1 7
A C = √ (3 - 5 ) ² + ( - 3- 5 ) =2 √ 1 7
P Δ A BC = 4 + 2√ 1 7 + 2 √1 7 = 4 + 4 √ 17 ( b ) c o s B = ( 2 √ 1 7 ) ² +4 ² - ( 2 √ 1 7 )² = 1 6 = 1 ⇒ < B = 7 6 ⁰
2 · 2 √ 1 7 · 4 1 6√ 1 7 √ 17
Изобразите на координатной плоскости множество решений системы неравенств {x^2+y^2<=9, {y-x<=1
Решение: Первое неравенство изображается кругом с центром в начале координат и радиусом. равным 5. Второе неравенство у>=х+2--это полуплоскость выше прямой у=х=2 и сама прямая. Нарисуй круг, проведи прямую и заштрихуй часть координатной плоскости выше прямой. Заштрихованная часть плоскости, ограниченная окружностью и прямой и будет множество решений системы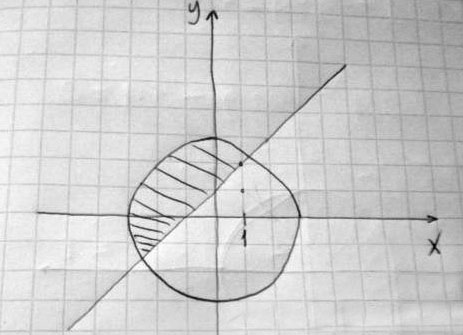
Отметьте и последовательно соедините на коорд. плоскости точки, координаты которых приведены в двоичной системе счисления: (101,101) (101,101000) (11001,101000) (11001,101) (10100,101) (10100,11110) (1010,11110) (1010,101) (101,101)
Решение: 1. Координаты первой точки (101;101)
В десятичной системе - (5; 5)
Т.к. 101 = 1×2^2 + 0×2^1 + 1×2^0 = 4+0+1 = 5
2. Координаты второй точки (101; 101000)
Или в десятичной - (5; 40)
101 мы уже вычислили
101000 = 1×2^5 + 0×2^4 + 1×2^3 + 0×2^2 + 0×2^1 + 0×2^0 = 32+0+8+0+0+0 = 40
3. Координаты 3ей точки (11001; 101000)
В десятичной - (25; 40)
11001 = 1×2^4 + 1×2^3 + 0×2^2 + 0×2^1 + 1×2^0 = 16+8+0+0+1 = 25
4. Координаты 4й точки (11001; 101) или в десятичной - (25; 5)
5. Координаты 5й точки (10100; 101) или (20; 5)
10100 = 1×2^4 + 0×2^3 + 1×2^2 + 0×2^1 + 0×2^0 = 16+0+4+0+0 = 20
6. Координаты 6й точки (10100; 11110) или (20; 30)
11110 = 1×2^4 + 1×2^3 + 1×2^2 + 1×2^1 + 0×2^0 = 16+8+4+2+0 = 30
7. Координаты 7й (1010; 11110) или (10; 30)
1010 = 1×2^3 + 0×2^2 +1×2^1 + 0×2^0 = 8+0+2+0 = 10
8. Координаты 8й (1010; 101), т.е. (10; 5)
9. И координаты 9й те же, что и у первой (5; 5)
10. При соединении точек получится замкнутая фигура.Начертите прямоугольную систему координат и постройте точки с заданными,координатами:1) х=2, у=3 3) х=-4, у=-2 5) х=-1, у=0
Решение: Решение см. на рисунке:
В одній системі координат побудуйте графіки функцій і вкажіть координати точок їх перетину у=2х+6. і. у=х+3
Решение: Спочатку треба написати : у=2х+6 - лінійна функція графіком якої є пряма. Малюємо табличку для значення х і у:1) х=1;у=8 2)х=2;у=10. Далі птшемо: у=х+3- лвнійна функція, графіком якої є пряма. Малюємо знову табличку з такими значеннчми:1)х=1;у=4 2)х=2;у=5. Далі малюємо два графіки на одній площині. Звідси, можна побачити точку перетину графіків (точку А), яка має координати А(-3;0)Напишите решение системы неравенств в виде числового промежутка и изобразите его на координатной прямой
2) {х > 3
{х < 6
4) {2х+3>х-1
{5х -22 <х +2
Решение: 2) все числа от 3 до 6, не включая 3 и 6 (на прямой отметьте точки 3 и 6,
не закрашивая их, заштрихуйте расстояние от 3 до 6)
4) 2x+3>x-1, x>-4
5x-221) Вычислить координаты точек пересечения прямых y=3x-4 и y=5x-10 2)Решите систему неравенства 5x+4<0 3x+1.5>0
Решение: 1) делаем систему 3х-у=4 и 5х-у=10решение
из 3х-у=4 Вычитаем 5х-у=10 И получаем -2х=-6, х=3, у=3*3-4=5 Ответ. (3;5)
мы меняем местами b и у и получаем систему, потому что у=кх+b
1)$$ \begin{cases} y=3x-4\\y=5x-10\\ \end{cases}\\ 3x-4=5x-10\\ -2x=-6\\ x=3\\ \begin{cases} x=3\\y=5 \end{cases} $$
Ответ:(3;5)
2)$$ \begin{cases} 5x+4<0\\3x+1,5>0\\ \end{cases}\\ \begin{cases} 5x<-4\\3x>-1,5\\ \end{cases}\\ \begin{cases} x<-0,8\\x>-0,5 \end{cases} $$
Ответ:(-0,8;-0,5)
По стройте в одной системе координат графики ф-й y=x-2;
y=-2x-2;
y=-2.
1) в какой точке каждый из этих графиков перечеркивает ось y,ось x;
2) каково взаимное расположение графиков?.
Решение: Составьте таблицу для каждого уравнения. Берете значение Х, и вычисляете значение Y. По две точки для каждого графика. А функция y = -2, это прямая проведенная через точку по линии Y -2. Проведите линии и все станет понятно.Номер 1
1)
Ох (2;0)
Оу (0;-2)
2)
Ох (-1;0)
Оу (0;-2)
3)
Ох не пересекает
Оу (0;-2)
Номер 2
Пересекаются
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...