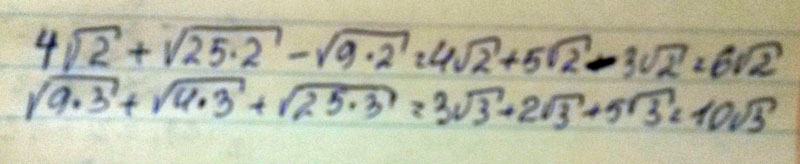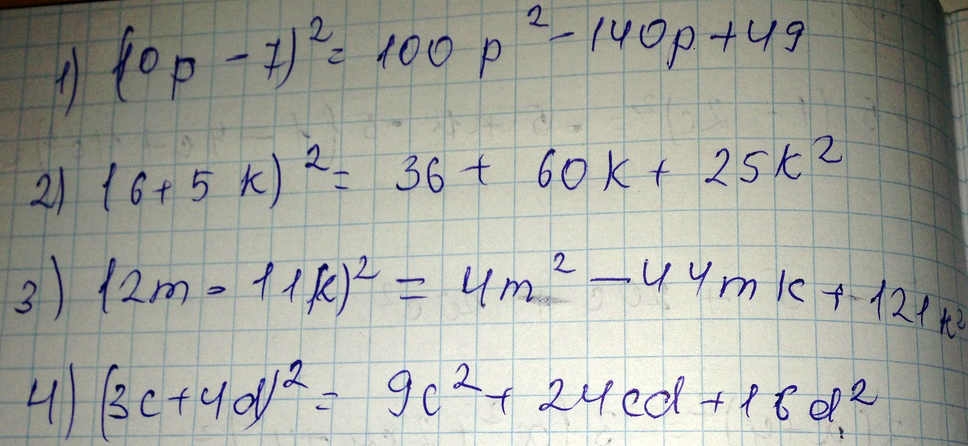многочлен »

представьте в виде многочлена - страница 10

  • 1Сколько цел. чисел заключено между числами √5 и√55 и √6и√66
    2Представьте в виде многочлена выражение 2(x-3)²+12x и 7(x-p)²+14xp
    3упр (a-6)(a+9)-(a-4)(a-2) и(2a+b)(a-b)-(2a²-b²)
    4 используя свойства арифм. квадрат. корня вычислите:4√2+√50-√18 и √27+√12+√75


    Решение: √5 и√55. 2<√5<3
    7<√55<8.
    значит между этими числами лежат целые числа: 3;4;5;6;7. то есть 5 числа.
    √6и√66. 2<√6<3
    8<√66<9. числа (3;4;5;6;7;8) то есть -6 чисел.
    2) 2(x-3)²+12x=2х^2-+18
    7(x-p)²+14xp=х^2+р^2
    3) (a-6)(a+9)-(a-4)(a-2)= а^2-6а+8.
    (2a+b)(a-b)-(2a²-b²)= 2а^2+ав-2ав-в^2-2а^2+в^2= -ав.
    4 используя свойства арифм. квадрат. корня вычислите:
    4√2+√50-√18=4\/2+5\/2-3\/2=
    6\/2
    √27+√12+√75=3\/3+2\/3+5\/3=10\/3.

    1) 3, 4, 5, 6, 7 - пять чисел
    3, 4, 5, 6, 7, 8 - шесть чисел
    2) 2(х²-6х+9)+12х=2х²-12х+18+12х=2х²+18
    7(х²-2рх+р²)+14хр=7х²-14хр+7р²+14хр=7х²+7р²
    3) a²+9a-6a-54-a²+2a+4a-8=9a-62
    2a²-2ab+ab-b²-2a²+b²= -ab
    4) в фотке:

    и ....

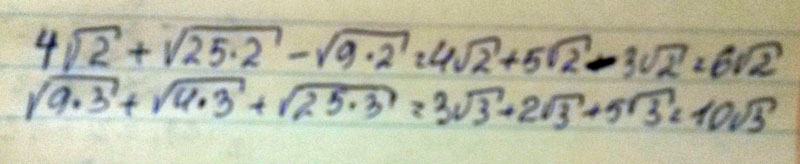
  • Представьте в виде многочлена выражение:
    а) (10p-7)2;
    б) (6+5k)2;
    в) (2m-11k)2
    г) (3c+4d)2


    Решение: a) Выражение: (10*p-7)^2=
    =100*p^2-140*p+49
    b) Выражение: (6+5*k)^2=
    =36+60*k+25*k^2
    c) Выражение: (2*m-11*k)^2=
    =4*m^2-44*m*k+121*k^2
    d) Выражение: (3*c+4*d)^2=
    =9*c^2+24*c*d+16*d^2

    -

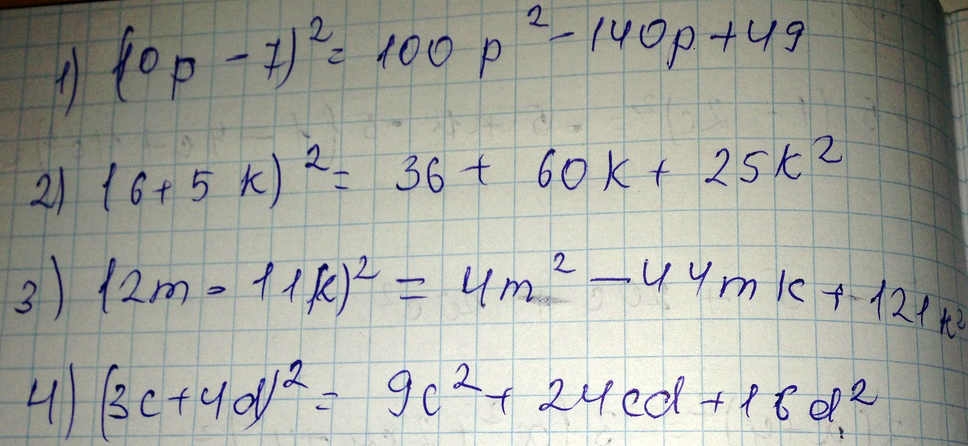
    a  Выражение p- p - p b  Выражение k k k c  Выражение m- k m - m k k d  Выражение c d c c d d -...

  • Произведение многочленов.
    Выполни умножение:
    а) (а+2)(х+6)
    б) (4-b)(d+3)
    в) (х+4)(3а-2)
    г) (4-b)(b+3)
    д) (3-7y)(2y-8)
    Представьте в виде многочлена выражение:
    а)\( (2x^{2}+4)(8 x^{2}-3) \)
    б)\( (y^{2}-7)( y^{2}+7) \)
    в)\( ( x^{2}-4)(x+3) \)
    г)\( ( 2c^{2}-c+6)(c+5) \)
    д)\( (a-3)( 3a^{2}-5a+2) \)


    Решение: $$ (a+2)(x+6)=ax+2x+6a+12; \\ (4-b)(d+3)=4d-bd-3b+12; \\ (x+4)(3a-2)=3ax+12a-2x-8; \\ (4-b)(b+3)=12-3b+4b-b^{2}=12+b-b^2; \\ (3-7y)(2y-8)=6y-14y^2+56y-24=62y-14y^2-24; \\ (2 x^{2} +4)(8 x^{2} -3)=16 x^{4}+26 x^{2} -12; \\ (y^{2}-7)(y^2+7)= x^{4}-49; \\ ( x^{2} -4)(x+3)= x^{3}+3 x^{2} -4x-12; \\ (2 c^{2}-c+6 )(c+5)=2 c^{3}-c^2+6c+10c^2-5c+30=2 c^{3}+9c^2+c+30; \\ (a-3)(3a^2-5a+2)=3a^3-9a^2-5a^2+15a+2a-6=3a^3-14a^2+17a-6. $$

<< < 8910