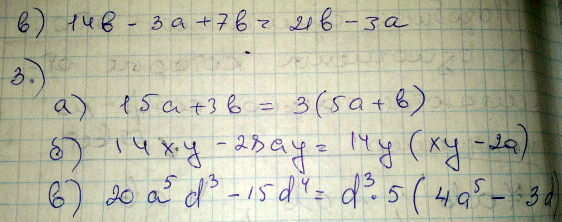многочлен »

преобразуйте в многочлен стандартного вида - страница 8

  • Запишите многочлен в стандартном виде : в) 14b-(3a-7b) 3 Вынесите за скобки общий множитель многочлена. а) 15а+3b б) 14xy-28ay в)20а5d3-15d4


    Решение: В) Многочлен в стандартном виде-это, когда все скобки раскрыты и никаких вычислений сделать нельзя
    14b-(3a-7b)
    14b-3a+7b=21b-3a
    а) 15а+3b =3(5а-b)
     б) 14xy-28ay=14y(x-2a)
    в)20а5d3-15d4 =300ad-60d=60d(5a-1)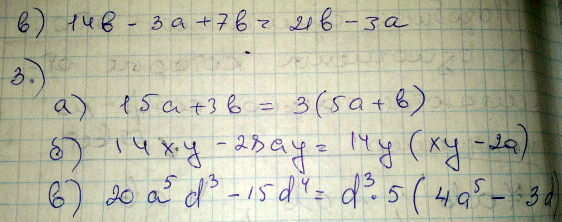В Многочлен в стандартном виде-это когда все скобки раскрыты и никаких вычислений сделать нельзя b- a- b b- a b b- aа а b  а-b  б xy- ay y x- a в а d - d   ad- d d a-...

  • 1. Записать в стандартном виде многочлен : 5х·3у²-2х²у-4ху·7у+0,5ух·5х
    2. Преобразовать в многочлен стандартного вида : (у³+у²-у)-(у²+у-1)
    3. Вычислить значение выражения : 3х²-(7ху-4х²)+(5ху-7х²), при х=0,3 ; у= -10
    4. Упростить выражение : (4а²)²-2а³(1+8а)
    5. Упростить выражение : (а+b)(а+2)-(а-b)(а-2)-2аb
    6. Раскрыть скобки используя соответствующее правило : а) 3а²+(а-5) ; б) 5-(4а+5)
    7. Упростить выражение : а) х-(3х+5)+(2х-4) ; б) (3а²-4b+5)+(2b-а²-1)
    8. Решить уравнение : (3х-5)+(2х-7)=-2
    9. Выполнить умножение: а) -4у(2х-5у+1); б) 8а²(а-3а³)
    10. Упростить выражение : а) 5(х-8)-2(5+х) ; б) х(х²+х-2)-х²(х-1)
    11. Упростить выраж. : у²(у³+у-2)-у(у³+1)+2у²-у³


    Решение: 1. Записать в стандартном виде многочлен : 5х·3у²-2х²у-4ху·7у+0,5ух·5х=15ху²-2х²у-28ху²+2,5х²у=-13ху²+0,5х²у
    2. Преобразовать в многочлен стандартного вида : (у³+у²-у)-(у²+у-1)=у³+у²-у-у²-у+1=у³-2у+1
    3. Вычислить значение выражения : 3х²-(7ху-4х²)+(5ху-7х²), при х=0,3 ; у= -10
    3х²-(7ху-4х²)+(5ху-7х²)=3х²-7ху+4х²+5ху-7х²=-2ху     -2*0,3*(-10)=6
    4. Упростить выражение : (4а²)²-2а³(1+8а)=16а^4-2а³-16a^4=-2а³
    5. Упростить выражение : (а+b)(а+2)-(а-b)(а-2)-2аb=а²+2a+ab+2b-а²+2a+ab-2b-2аb=4a
    6. Раскрыть скобки используя соответствующее правило : а) 3а²+(а-5)=3а²+а-5  ; б) 5-(4а+5)=5-4а-5=-4a
    7. Упростить выражение : а) х-(3х+5)+(2х-4)=х-3х-5+2х-4=-9  ; б) (3а²-4b+5)+(2b-а²-1)=3а²-4b+5+2b-а²-1=2а²-2b+4
    8. Решить уравнение : 3х-5+2х-7=-2
    5х-12=-2
    5x=10
    x=2
    9. Выполнить умножение: а) -4у(2х-5у+1)=-8xy+20y²-4y; б) 8а²(а-3а³)=8a³-24a^5
    10. Упростить выражение : а) 5(х-8)-2(5+х)=5x-40-10-2x=3x-50 ; б) х(х²+х-2)-х²(х-1)=x³+x-2x-x³+x²=2x²-2x
    11. Упростить выраж. : у²(у³+у-2)-у(у³+1)+2у²-у³ =y^5+y³-2y²-y^4-y+2y²-y³=y^5-y^4-y
    ^ - знак степени

  • На примере многочлена 5xy²-x²y-2xy*3y+7x²y объясните, как приводят многочлен к стандартному виду


    Решение: Чтобы привести многочлен к стандартному виду нужно:
    1) перемножить все числовые множители и поставить их произведение на первое место
    2) перемножить все имеющиеся степени с одним буквенным основанием
    3) перемножить все имеющиеся степени с другим буквенным основанием
    пример:
    5xy²-x²y-2xy*3y+7x²y=
    5xy²-x²y-6xy²+7x²y=
    -xy²+6x²y
    многочлен приведен к стандартному виду

  • x в 4 степени +4x в квадрате y- x в 4 степени +y в 4 сстепени+6x в квадрате y в квадрате +y в 4 степени Нужно привести многочлен к стандартному виду и найдите его значение при y=1,x=-3


    Решение: (x^4)+4(x^2)y -(x^4)+(y^4)+6(x^2)(y^2)+(y^4)=4(x^2)y+6(x^2)(y^2)+2(y^4)=4*9*1+6*9*1+2*1=92

    Вот такое уравнение получилось

    $$ x^4+4x^2y-x^4+y^4+6x^2y^2+y^4=4x^2y+6x^2y^2+2y^4 \\ 4\cdot(-3)^2\cdot1+6\cdot(-3)^2\cdot1^2+2\cdot1^4=4\cdot9+6\cdot9+2=36+54+2=92 $$

    $$ x^{4}+4x^{2}y-x^{4}+y^{4}+6x^{2}y^{2}+y^{4}=(x^{4}-x^{4})+4x^{2}y+6x^{2}y^{2}+(y^{4}+y^{4})= 4x^{2}y+6x^{2}y^{2}+2y^{4} $$

    ===========================================================

    при y=1,x=-3

    $$ 4\cdot(-3)^{2}\cdot1+6\cdot(-3)^{2}\cdot1^{2}+2\cdot1^{4}=4\cdot9\cdot1+6\cdot9\cdot1+2\cdot1=36+54+2=92 $$

  • 1) преобразовать в многочлен стандартного вида:
    (3х+у)^2+(х-у)(у+х)
    2) упростить выражение
    6) задача
    разность 2 чисел равна 12. Найдите эти числа, если 2/5 первого числа составляют 4/7 другого?


    Решение: 1)
    $$ (3x+y)^2+(x-y)(y+x)=(3x+y)(3x+y)+(x-y)(y+x)= \\ =9x^2+3xy+3xy+y^2+xy+x^2-y^2-xy=9x^2+6xy+x^2 $$
    2)
    $$ \frac{x}{x-y} :( \frac{x+y}{y} + \frac{y}{x-y} ) \\ \\ \\ 1)\frac{x+y}{y} + \frac{y}{x-y}= \frac{(x+y)(x-y)+y^2}{y(x-y)} = \\ \\ =\frac{x^2-xy+xy-y^2+y^2}{y(x-y)} =\frac{x^2}{y(x-y)} \\ \\ 2)\frac{x}{x-y} :\frac{x^2}{y(x-y)} =\frac{x}{x-y} *\frac{y(x-y)}{x^2} = \frac{y}{x} $$
    6)
    $$ \left \{{x-y=12} \atop {\frac{2x}{5}=\frac{4y}{7}} \right. \\ \left \{{x-y=12} \atop {7*2x=5*4y}\right. \\ \left \{{x-y=12} \atop {14x=20y} \right. \\ \left \{{x-y=12} \atop {x=\frac{20y}{14}=\frac{10y}{7}} \right. \\ \frac{10y}{7}-y=12 \\ \frac{10y-7y}{7}=12 \\ 3y=12*7 \\ y= \frac{12*7}{3}=4*7=28 \\ x-28=12 \\ x=12+28 \\ x=40 $$

<< < 678 9 > >>