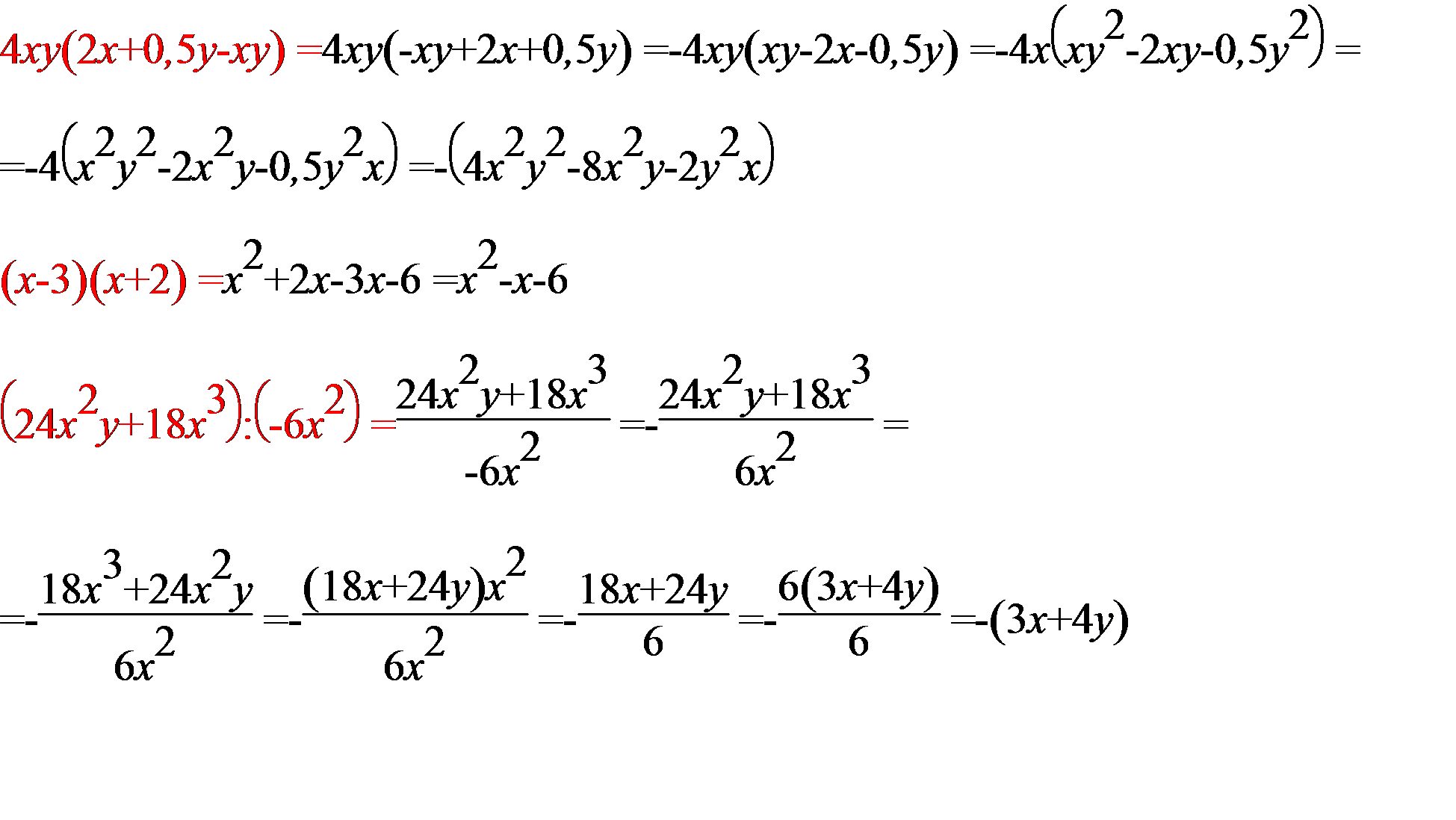многочлен »

преобразуйте в многочлен стандартного вида - страница 7

  • Преобразуйте заданное выражение в многочлен стандартного вида: а) 4xy(2x + 0,5y - xy) б) (x - 3)(x + 2) в) (24x^2y + 18 x^3) : (-6x^2)


    Решение: файл

    -

    а) 4ху(2х+0,5у-ху)  = 8х^2у+2ху^2-4х^2у^2

    б) (x - 3)(x + 2) = х^2-3х+2х-6 = х^2-х-6

    в) (24x^2y + 18 x^3) : (-6x^2) = 6х^2(4у+3х) : (-6x^2) = -(4у+3х) = 3х-4у

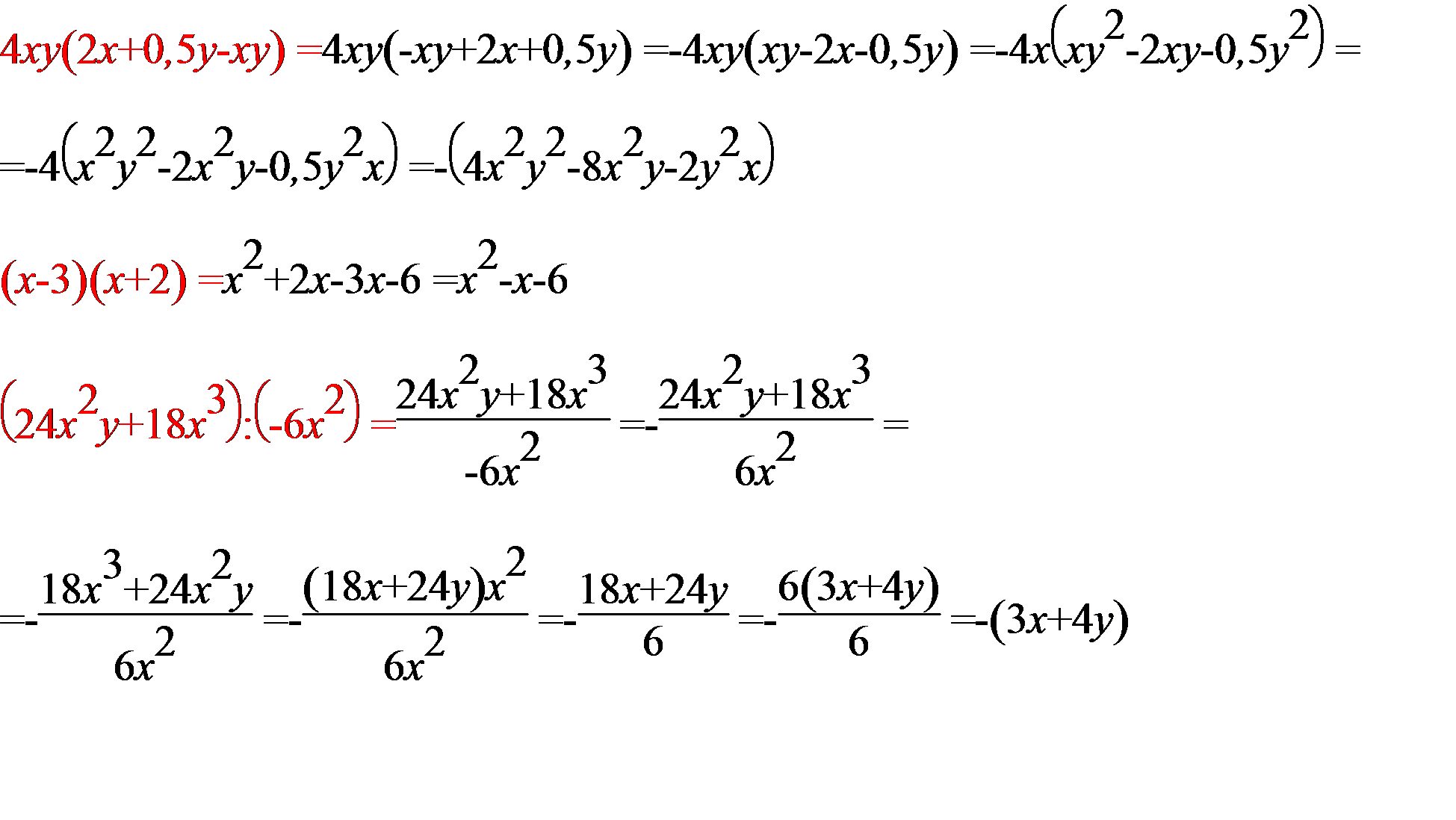
    файл -а ху х у-ху   х у ху - х у б x - x х - х х- х -х- в x y x - x х у х   - x - у х х- у...

  • 1. Запишите одночлен в стандардатном виде:
    a) -3.5ab^3c^2 × 1.6a^3bc б) (-2 (целых)3/4)b^4c^2×(-8/33) b^2c^2
    2. Упростите алгебраическое выражение: (x-1)(x-2)(x+3)-(x+1)(x+2)(x-3).
    3. Преобразуйте алгебраическое выражение в многочлен стандартного вида: a) (2b+a^3)(a^3-2b) б) (x^2+y^2)(y^4-x^2y^2+x^4).
    4. Разложите на множители: a) 16ab^3-20a^2b^2 б) 18x^4y^2-12x^5y^3x^3
    В) mn-2m+4n-8 г)x^2+3xy-4y^2.
    5. Докажите алгебраическое равенство
    (x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)=x^8-1.


    Решение: 1. а) $$ -5,6a^{4} b^{4} c^{3} $$
        б) $$ \frac{2}{3}b^{6} c^{4} $$
    2. $$ (x-3)((x-1)(x-2) - (x+1)(x+2)) $$
        $$ (x-3)( x^{2} -2x-x+2- x^{2} -2x-x-2) $$
        $$ -6x(x-3) $$
        $$ 18-6 x^{2} $$
    3. а) $$ ( a^{3} - 2b)( a^{3} +2b) = a^{6} - 4 b^{2} $$ (разница квадратов)
        б) $$ x^{6} + y^{6} $$ (сумма кубов)
    4. а) $$ 4a b^{2} (4b - 5a) $$
       б) $$ 6x^{4} y^{2} (3-2xy) $$
       в) $$ n(m+4) - 2(m+4) = (n-2)(m+4) $$
    5. Просто раскрываем скобки слева и приходим к равенству. При умножении иксов степени складываются.
      

  • Запишите в виде многочлена стандартного вида: 3(4а-1)-(12а+3)+2а; х²-2х-8-(2х²+х-7);
    Найдите значение выражения: \( 2,5a + a^2\) при a = 7,5
    Решите уравнение: \(a) x-2x^2=0 \\ b) 2x^2 + 8x =0\)


    Решение: $$ 3(4a-1)-(12a+3)+2a=12a-3-12a-3+2a=\\=(12a-12a+2a)+(-3-3)=2a-6 $$

    б) $$ x^{2}-2x-8-(2x^{2}+x-7)=x^{2}-2x-8-2x^{2}-x+7=\\=(x^{2}-2x^{2})+(-2x-x)+(-8+7)=-x^{2}-3x-1=-(x^{2}+3x+1) $$

    $$ 2,5a+a^{2} $$

    при $$ a=7,5 $$

    для начала упростим данное выражение

    $$ 2,5a+a^{2}=a(2,5+a) $$

    при $$ a=7,5 $$; $$ 7,5\cdot(2,5+7,5)=7,5\cdot10=75 $$

    а) $$ x-2x^{2}=0 \\ x(1-2x)=0 \\ x_{1}=0 \\ 1-2x=0 \\ 2x=1 \\ x=1:2 \\ x_{2}=\frac{1}{2}=0,5 $$

    Ответ: $$ x_{1}=0 $$; $$ x_{2}=0,5 $$

    б) $$ 2x^{2}+8x=0 \\ 2x(x+4)=0 \\ 2x=0 \\ x=0:2 \\ x_{1}=0 \\ x+4=0 \\ x_{2}=-4 $$

    Ответ: $$ x_{1}=0 $$; $$ x_{2}=-4 $$

  • Записать в виде многочлена стандартного вида 2(х/2-1)(1+х/2)


    Решение: $$ 2( \frac{x}{2}-1)( 1+\frac{x}{2}) = 2( \frac{x}{2}-1)( \frac{x}{2}+1) = 2* (\frac{x^2}{4} -1) = 2* \frac{x^2-4}{4}= \frac{x^2-4}{2}= \frac{1}{2} x^2-2 $$

    frac x - frac x frac x - frac x frac x - frac x - frac x - frac x -...

  • Запишите в виде многочлена стандартного вида (2x+2y)(2x-y)-(2x+3xy)


    Решение: (2х+ 2у)(2х - у) - (2х + 3ху) = 4х² - 2ху + 4ху - 2у² - 2х - 3ху = 4х² - 2у² - ху - 2х

    Две передние скобки просто перемножаются получается:
    4x  в кв. + 4xy -2xy - 4y в кв.
    Вторые скобки раскрываем:
    Учитывай минус
    поэтому -2x-3xy
    Получается
    4x в кв. + 4xy - 2xy - 4y в кв. 2x - 3xy
    Дальше приводим подобные
    4ху - 2ху - 3ху = -1ху
    Так теперь
    4х в кв. 4у в кв. 1ху - 2х
    получается
    (4х в кв. 1ху - 4у в кв.) - 2х

<< < 567 8 9 > >>