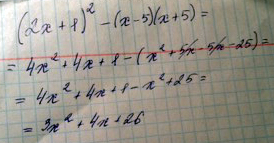преобразуйте в многочлен стандартного вида - страница 5
Преобразуйте в многочлен стандартного вида выражения:
(2х-3)²; (0,2с²-0,6)²; (4х-у)²-(х+3у)²; (3х+5)²; (0,3а²+0,7)²(х+4у)²-(3х-у)²
Решение: (2х-3)² = 4x^2 - 12x + 9
(0,2с²-0,6)² = 0,04c^4 - 0,24c^2 + 0,36
(4х-у)²-(х+3у)² = 16x^2 - 8xy + y^2 - x^2 - 6xy - 9 y^2 = 15x^2 -14xy-8y^2
(3х+5)² = 9x^2 + 30x + 25
(0,3а²+0,7)²(х+4у)²-(3х-у)² = (0,09a^4 + 0,42a^2 + 0,49)(x^2+8xy+16y^2) -(9x^2-6xy+y^2) = 0,09a^4x^2 + 0,42a^2x^2 + 0,49x^2 + 0,72a^4xy + 3,36a^2xy + 3,92xy + 1,44a^4y^2 + 6,72a^2y^2 +7,84y^2-9x^2+6xy-y^2 = 0.09a^4x^2 + +0,42a^2x^2 - 8,51x^2+ 0,72a^4xy + 3,36a^2xy + 9,92xy + 1,44a^4y^2 + +6,72a^2y^2 + 6,84y^2
Преобразуйте в многочлен стандартного вида:
(2х+1)2- (х+5)∙(х-5).
Решение: Ответ прикреплен.$$ (2x+1)^2-(x+5)(x-5)=4x^2+4x+1-(x^2-25)= \\ 4x^2+4x+1-x^2+25=3x^2+4x+26 \\ $$. _Первую скобку нужно раскрыть по формуле: $$ (a+b)^2=a^2+2ab+b^2 $$. А произведение (х-5)(х+5) свернуть по формуле разности квадратов:$$ (a-b)(a+b)=a^2-b^2 $$. Далее просто приводим подобные слагаемые и получаем стандартный вид многочлена.
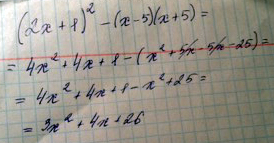
№1
преобразуйте в многочлен стандартного вида
(24x²y+18x³):(-6x²)
№2
докажите, что данное выражение не зависит от значения переменной
5x³-5(x+2)(x²-2x+4)
№3
решите уравнение
(x-1)³-x²(x-3)=8
№4
найдите наибольшее значение многочлена
p(x)=19-8x-x²
Решение: №1.
$$ \frac{24x^2y+18x^3}{-6x^2}=\frac{24x^2y}{-6x^2}+\frac{18x^3}{-6x^2}=-4y-3x $$
№2.
$$ 5x^3-5(x+2)(x^2-2x+4)=5x^3-5(x^3-2x^2+4x+2x^2-4x+8)=\\=5x^3-5x^3-40=-40 $$
№3.
$$ (x-1)^3-x^2(x-3)=8\\ x^3-3x^2+3x-1-x^3+3x^2-8=0\\ 3x=9\\x=3 $$
№4.
$$ p(x)=19-8x-x^2\\ p’(x)=-8-2x=0\\x=-4 - to4kaMAXIMUMA\\p(-4)=19-8*(-4)-(-4^2)=19+32-16=35 $$
1.
$$ (24x^{2}y+18x^{3}):(-6x^{2})=\\\\ =\frac{6x^{2}(4y+3x)}{-6x^{2}}=\\\\ =-3x-4y $$
2.
$$ 5x^{3}-5(x+2)(x^{2}-2x+4)=\\\\ =5x^{3}-5(x^{3}-2x^{2}+4x+2x^{2}-4x+8)=\\\\ =5x^{3}-5(x^{3}+8)=\\\\ =5x^{3}-5x^{3}-40=\\\\ =-40 $$
- не зависит от x.
3.
$$ (x-1)^{3}-x^{2}(x-3)=8 \\\\ x^{3}-3x^{2}+3x-1-x^{3}+3x^{2}=8 \\\\ 3x-1=8 \\\\ 3x=9 \\\\ x=3 $$
4.
$$ p(x)=19-8x-x^{2} \\\\ p(x)=-(x^{2}+8x+16)+16+19 \\\\ p(x)=-(x+4)^{2}+35 $$
Очевидно, что наибольшее значение p(x) примет при $$ (x+4)^{2}=0 $$.
Ответ: 35.
РЕШИТЕ 1) Преобразуйте в многочлен стандартного вида
А) (а+7b)(7b-а)
Б) (m+5)²-3m(m-4)
Решение: A) (a+7b)(7b-a) = (7b+a)(7b-a) = 49b^2-a^2. B) (m+5)^2-3m(m-4) = m^2+10m+25-3m^2+12m = -2m^2+22m+25.A) (a+7b)(7b-a)=(7b+a)(7b-a)=49b^2-a^2.
Б) (m+5)^2-3m(m-4)=m^2+10m+25-3m^2+12m=
=-2m^2+22m+25=-2(m-11+9 корней из 38/2)(m-11-9 корней из 38/2).
-2m^2+22m+25=0
D=484-4*(-2)*25=484+200=684
m1=-22+18 корней из 38/-4=-2(11-9 корней из 38)/-4=11-9 корней из 38/2.
m2=-22-18 корне из 38/-4=-2(11+9 корней из
38/-4=11+9 корней из 38/2.(^2-ЭТО ЗНАЧИТ ВТОРАЯ СТЕПЕНЬ)
1. Преобразуйте в многочлен стандартного вида: а) (10х+3у)(3у-10х); б) 3а(4-5а)-(а-4)^2 (вторая степень)
2. Разложите на множители: а) а(2b-c)+6ab-3acб) 3a^3-3a^2-2a+2в) (b-6)^2-16b^2
3. Дана функция у=5-3х а) Найдите значение функции, соответствующие значению аргумента, равному -2. б) Найдите значение аргумента, которому соответствует значение функции, равное -16.
Решение: 1. а) (10х+3у)(3у-10х)=(3у+10х)(3у-10х)=9у^2-100x^2
б) 3а(4-5а)-(а-4)^2=12а-15a^2-(a^2-8а+16)=12а-15а^2-а^2+8а-16=20а-16а^2-16
2. а) а(2b-c)+6ab-3ac=2ab-ac+6ab-3ac=8ab-4ac=4a(2b-c)
б) 3a^3-3a^2-2a+2=3а^2(a-1)-2(a-1)=(a-1)(3a^2-1)
в) (b-6)^2-16b^2=b^2-12b+36-16b^2=-15b^2-12b+36=-(b+2)(b-1,2)=(b+2)(1,2-b)
3. у=5-3х
а) х=-2 => у=5-3*(-2)=5+6=11
б) у=-16 => -16=5-3х
-16-5=-3х
-21=-3х
х=7