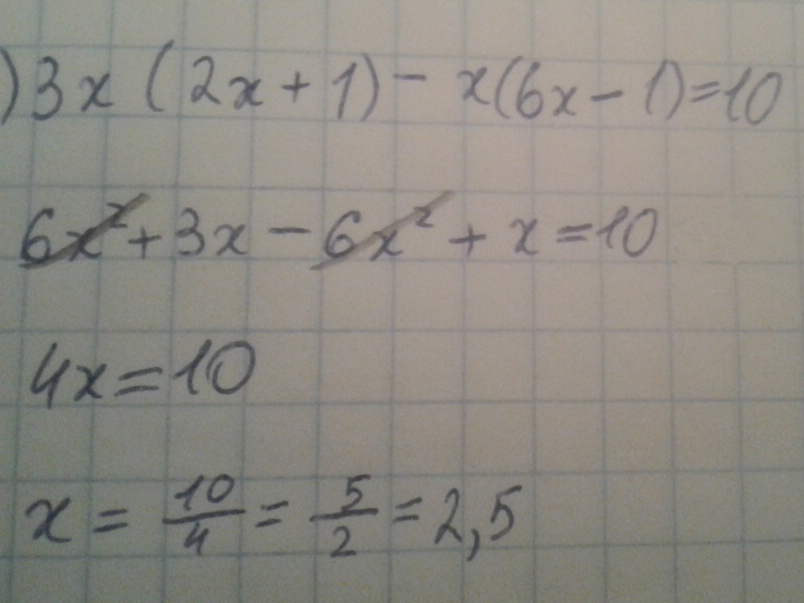преобразуйте в многочлен стандартного вида - страница 4
Решить уравнение
1. 3x(2x +1) - x(6x -1) = 10
Решение: 3x(2x+1)-x(6x-1)=10
6x²+3x-6x²+x=10
4x=10
x=2,5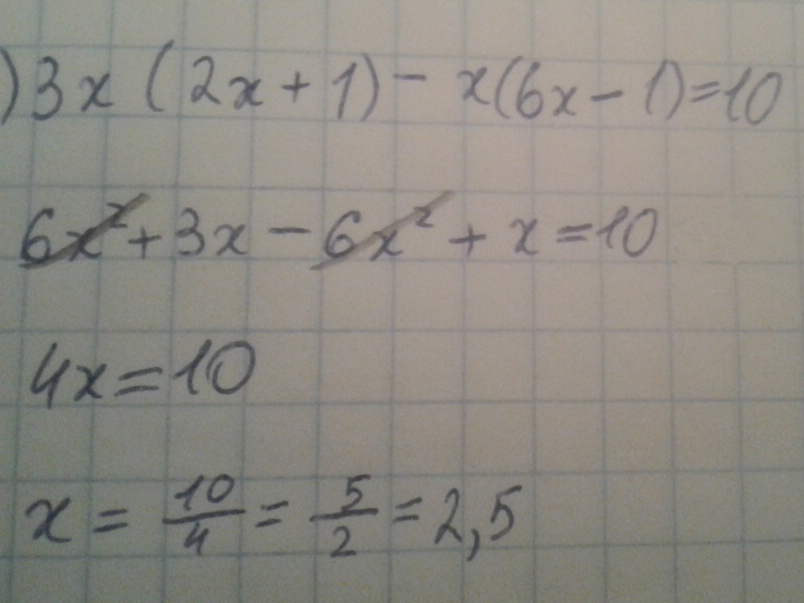
Преоброзуйте в многочлен стандартного вида: (x+8)^2 -4x(x-2)
Решение: (x+8)^2-4x(x-2)=x^2+16x+64-4x^2+8x=-3x^2+24x+64
P.S Поставь пж как лучшийДля начала раскрываем скобки, пользуемся формулой (a+b)^2=a^2+2ab+b^2
Итак:
(x+8)^2=x^2+16x+64
Затем, пользуемся распределительным свойством
a(b+c)=ab+ac
Итак:
-4x(x-2)=-4x^2+8
Теперь осталось отнять одно из другого и сократить
x^2+16x+64-4x^2+8x=-3x^2+24x+64Запишите многочлен в стандартном виде:
a) \( (x^{2}-3x+2)^{2}-(x^{2}-x)^{2} \)
b) \( (x+1)(x^{7}-x^{6}+.x^{2}+x-1) \)
c) \( (2-x)^{3}+(x-1)^{3} \)
d) \( (x^{5}-x^{4}+x^{3}-x^{2}+x-1) \\ (x^{5}+x^{4}+x^{3}+x^{2}+x+1) \)
Решение: A) $$ (x^{2}-3x+2)^{2}-(x^{2}-x)^{2} = \\ = (x^{2}-3x+2 - x^{2}+x )(x^{2}-3x+2 + x^{2}-x) = \\ =(-2x+2)(2x^{2}-4x+2)= \\ = -4x^{3} + 12x^{2}-12x+4 $$
b) $$ (x+1)(x^{7}-x^{6}+.x^{2}+x-1) = \\ = x^{8} - x^{7}+.x^{3}+x^{2}-x+x^{7}-x^{6}+.x^{2}+x-1=x^{8} - 1 $$
c) $$ (2-x)^{3}+(x-1)^{3}=8 - 12x + 6x^{2} - x^{3} + x^{3} - 3x^{2} + 3x - 1= \\ =3x^{2} - 9x + 7 $$
d) $$ (x^{5}-x^{4}+x^{3}-x^{2}+x-1)(x^{5}+x^{4}+x^{3}+x^{2}+x+1)= \\ =(x^{4}(x-1)+x^{2}(x-1)+(x-1))(x^{4}(x+1)+x^{2}(x+1)+(x+1))= \\ =(x-1)(x^{4}+x^{2}+1)(x + 1)(x^{4}+x^{2}+1)=(x^2 - 1)(x^{4}+x^{2}+1)^{2}= \\ =(x^8+2x^6+3x^4+2x^2+1)(x^2-1)= \\ =x^{10}+2x^8+3x^6+2x^4+x^2-x^8-2x^6-3x^4-2x^2-1= \ =x^{10}+x^8+x^6-x^4-x^2-1 $$
Преобразуйте в многочлен стандартного вида:
а) (2x + 5y)(5y - 2x);
б) 2a(3 - 2a) - (a-6)^2
написать ход решения.
Решение: Полагаю тут по формула сокращенного умножения.
а) (2х + 5у)(5у - 2х) = 25у² - 4х²
1) Просто возводим всё в квадрат.
б) 2а(3 - 2а) - (а - 6)² = 6а - 4а² - ( а² - 12а + 36 ) = 6а - 4а² - а² + 12а - 36 =
= - 5а² + 18а - 36.
1) Открываем первую скобку, а вторую преобразовываем с помощь формул сокращенного умножения.
2) Открываем скобку после первого действия и меняем знаки.
3) Приведем подобные слагаемые.Преобразуйте в многочлен стандартного вида:
а) а^2+(5а-b)^2=
б) 2(а-3)(а+3)=
в) (а-4)(а+4)(а^2+16)=
5. Решите уравнение:
а) 16с^2-49=0
б) (2х-5)^2-(2х-3)(2х+3)=0
Помоги с этим прошу
Решение: а) a^2 + 25a^2- 10ab +b^2= 26*a^2-10ab+b^2б) 2(а-3)(а+3)=2*a^2-18
в) (а-4)(а+4)(а^2+16)=(a^2-16)*(a^2+16)=a^4+256
а) 16с^2-49=0
16c^2=49
c^2=49/16
с=корень из 49/16
с=+7/4 и с=-7/4
б) (2х-5)^2-(2х-3)(2х+3)=0
расскрываем скобки
4x^2-20x+25 - (4x^2-9)=0
4x^2-20x+25 - 4x^2+9=0
-20x+34=0
-20x=-34
x=34/20
х=1.7
а)a^2+(25a^2-10ab+b^2),
a(a+25)-b(10a-b).
б)2(a^2+3a-3a-9),
2(a^2-9).
в)(a^2+4a-4a-16)(a^2+16),
(a^2-16)(a^2+16)=a^4-256.
Задание 5.
а)(4c-7)(4c+7)=0;
4с=7|4 => c=7/4
{
4с=-7|4 => с=-7/4.
б)(4x^2-20+25)-(4x^2+6x-6x-9)=
=4x^2-20+25-4x^2+6x-6x+9=
=-20х+34
-20х=-34|(-20)
х=1,7.
вот и всё=)