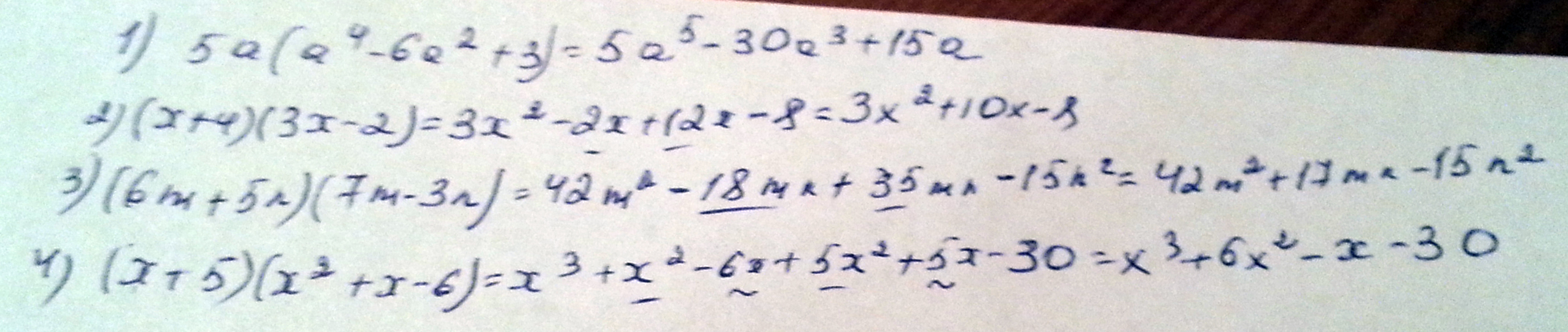преобразуйте в многочлен стандартного вида - страница 2

Преобразуй в многочленов стандартного вида: 1) (8xy-5y+2)+(3y-3-8xy). 1) 8xy-5y+2+3y-3-8xy 2) -2y-1 3)16xy-2y-1 4)-2y+5. найдите равность 2x²-x+4 и -3x²-2x+3. 1) 5x²-3x+1 2) 5x²+x+1 3) 5x²+x+7 4) -x²-3x+7. решение уравнения:5y-3-(4-2y)=3. 1)4,7 2)1 1,3 3) 3 1,3 4) 1 3,7 для каждого многочислителя нужно указать его степень a)3x²-x³-3x²+1 b)5x+4x-x v)6-2x-5x². найти значение многочлена -8a²-2ax-x²-(-4a²-2ax-x²)при a=-3,4 ,x=-2

Представьте в виде многочлена стандартного вида выражение:
5а(а4-6а2+3) - P.S (а4) - "а" в четвертой степени
(х+4) (3х-2)
(6m+5n) (7m-3n)
(х+5) (х2+х-6)

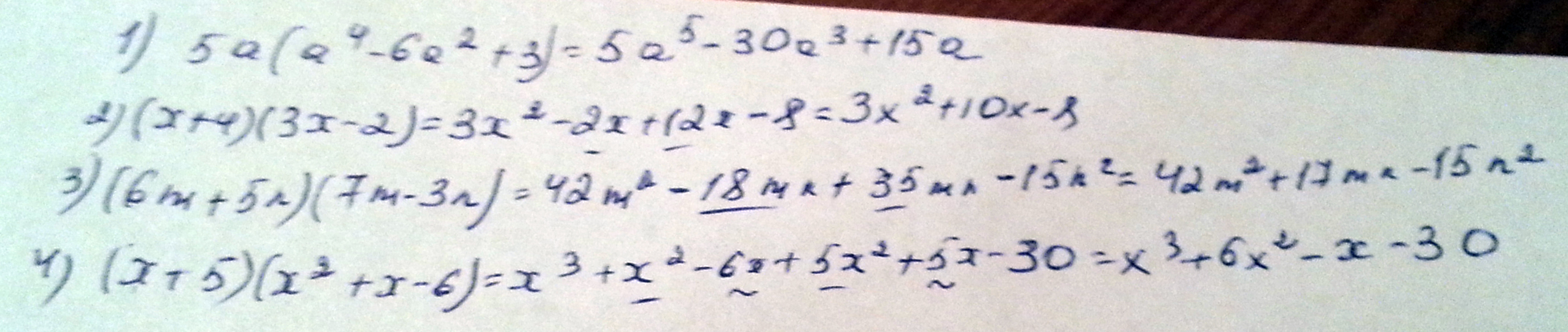
№4.
Представьте в виде многочлена стандартного вида выражение(7хво второй степени -4х+8)-(4хво второй степени +х-5)
№6
Упростите выражение
8х в 3степени умножить у в 4 степени умножить(-0.5х во 2 степени умножить у в 5 степени) это все в 3 степени
№8
Докажите, что значение выражения (7н+19)-(3+5н) кратно 2 при любом натуральном значении н

4)(7x²-4x+8)-(4x²+x-5)=7x²-4x+8-4x²-x+5=3x²-5x+13
6)8x³*y^4*(-0,5x²*y^5)³=8x³y^4*(-0,125x^6y^15)=-x^9y^19
8)[(7n+19)-(3+5n)]/2=(7n+19-3-5n)/2=(2n+16)/2=2(n+8)/2=n+8

Представьте многочлен в стандартном виде
-8p(в 4 степени)+12p(в 3 степени)+4p(в 4 степени)-8p(в квадрате)+3p(в квадрате)
Найдите значение многочлена
4a(в квадрате)-ab(в квадрате)-3a(в квадрате)b+ab(в квадрате)-ab+6 при a=-3, b=2
Представьте выражение в виде одночлена
-0,2a(в квадрате)b(в 3 степени)*(-5a(в квадрате)b(в квадрате))) и всё это в квадрате

Чтобы разложить квадратный многочлен на множители, нужно найти его корни

ax^2 + bx + c = a(x - x1)(x - x2), где x1 и x2 - корни

$$ 4p^{2}-12p+5\\ D = 144 - 4*4*5 = 144 - 80 = 64\\ p_{12} = \frac{12 ^{+}_{-}8}{8}\\ p_{1} =2,5\\ p_{2} =0,5\\ 4p^{2}-12p+5 = 4(p-2,5)(p-0,5) = (2p-5)(p-1) \\ -p^{2}(4p^{2}-12p+5) = -p^{2}(2p-5)(2p-1) = p^{2}(5-2p)(2p-1) $$

2)$$ 4a^{2}-ab^{2}-3a^{2}b+ab^{2} - ab +6=\\ \\ 4a^{2}-ab^{2}-3a^{2}b+ab^{2} - ab +6=\\ =4a^{2}-3a^{2}b - ab +6=\\ a=-3, b=2\\ =4(-3)^{2}-3(-3)^{2}*2 - (-3)*2 +6=\\ =4*9 -6*9+6+6=12 $$

3)$$ [-0,2a^{2}*b^{3}*(-5*a^{2}*b^{2})]^{2}=\\ =[(0,2*5)*(a^{2}*a^{2})*(b^{3}*b^{2})]^{2}=\\ =[a^{2+2}*b^{3+2}]^{2}=\\ =[a^{4}*b^{5}]^{2}=a^{4*2}*b^{5*2}=a^{8}*b^{10} $$

1. Приведите многочлены в стандартный вид и назовите их степень:
а)-3xy+9xy-12xy
б)8x3-11x+8x3-10x3+16x
в)15a5+a3-12+2a5-a3-30
2. Найдите сумму и разность данных многочленов:
а)(-3ab+6b-3c) и (7ab-6b+2c)
б)(8x2+11x-1) и (3+5x-5x2)
3. Докажите тождество.
а)a(b-x)+x(a+b)=b(a+x)
б)16-(a+3)(a+2)=4-(6+a)(a-1).
4. Решите уравнения:
а)(3x-1)2-9x2=-35
б)4(x-4)(x+8)=(3x+2)(x-5)+(x-1)(x+1).