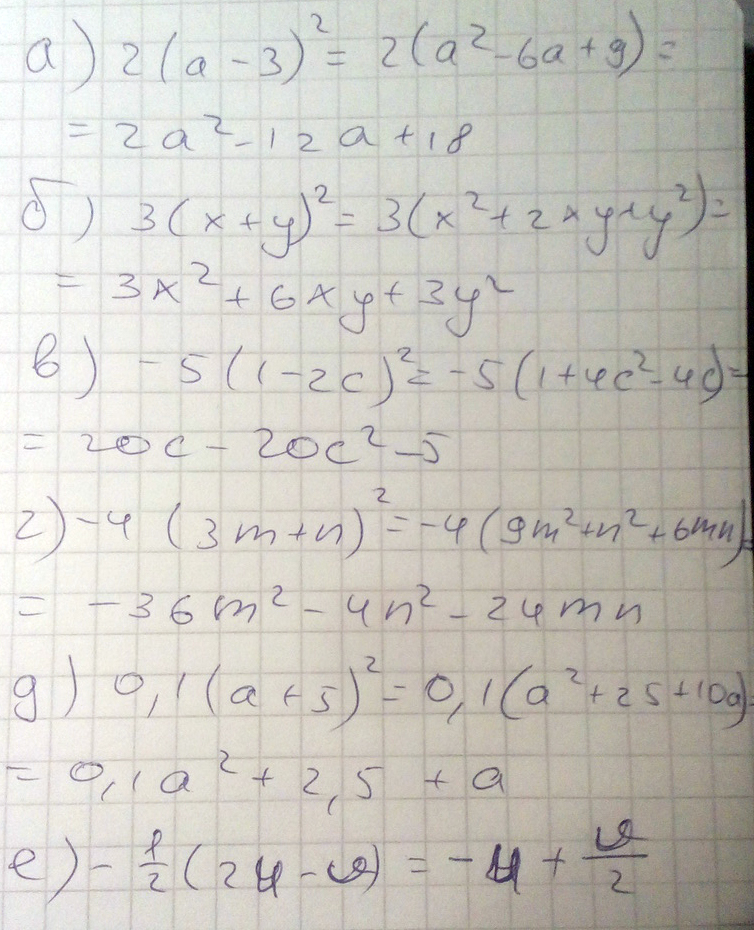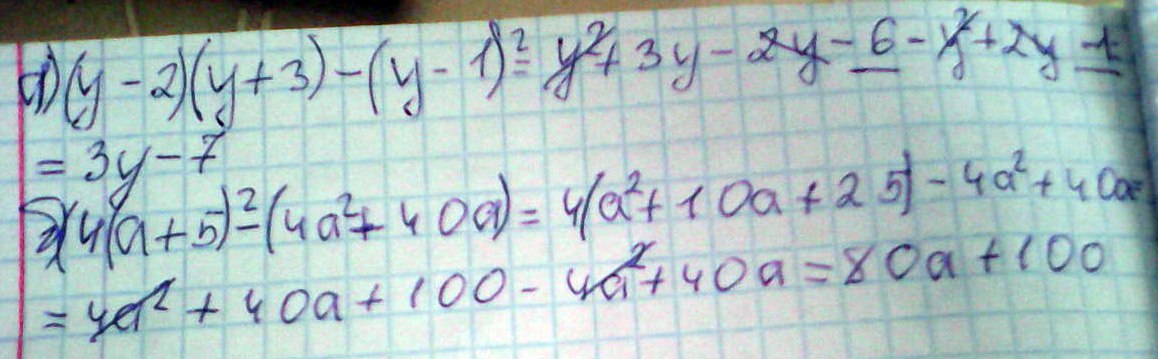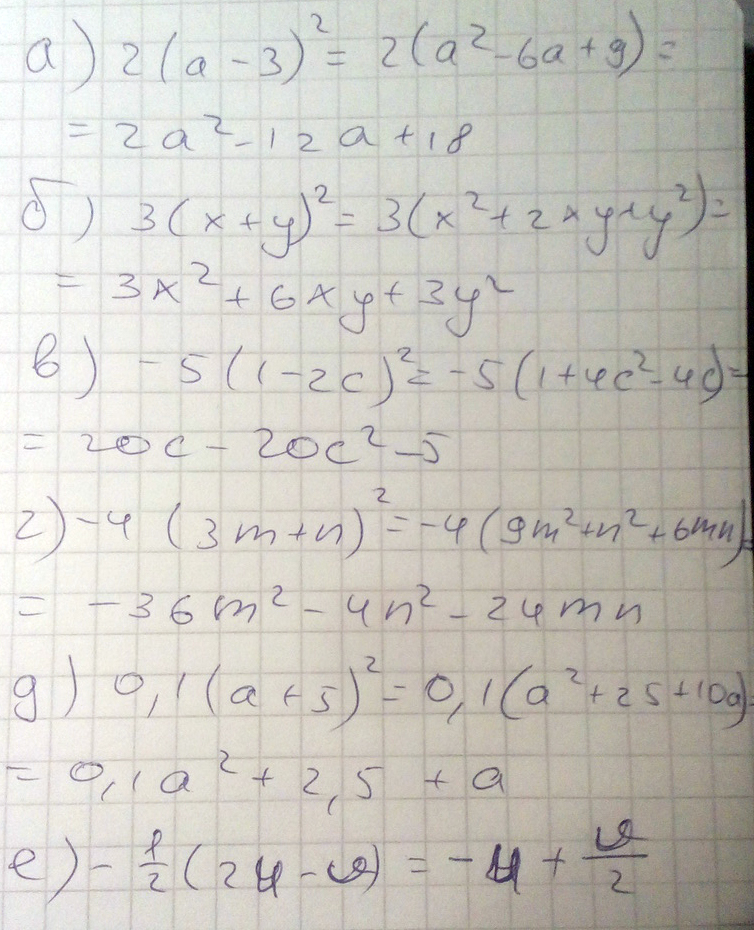многочлен »

преобразуйте в многочлен - страница 2

  • преобразуйте в многочлен
    (2A+3)(2A-3)
    (у-5б)(у+5б)
    (0,8х+у)(у-0,8х)
    (B+0.5)^2
    (а-2х)^2
    (аб-1)^2


    Решение: 1. (2а+3)(2а-3)=(2a)^2 - 3^2 = 4a^2 - 9 
    2. (у-5b)(у+5b)= y^2 - (5b)^2 = y^2 - 25b^2 
    3. (0,8х+у)(у-0,8х)= 0.8xy - 0.64x^2 + y^2 - 0.8xy = y^2 - 0.64x^2 
    4. (b+0,5)^2= b^2+2*0,5b+0,5^2 = b^2 + b + 0.25 
    5. (а-2х)^2= a^2-2*2ax+(2x)^2 = a^2 - 4ax +4x^2 
    6. (ab-1)^2 = ab^2-2ab+1^2 = a^2 + b^2 + ab +1

    Формулы сокращённого умножения)

    Если ещё не учили, то 1. (2а+3)(2а-3)=4a^2 - 6a + 6a - 9 = 4a^2 - 9 
    2. (у-5b)(у+5b)= y^2 + 5by -5by -25b^2 = y^2 - 25b^2 
    3. (0,8х+у)(у-0,8х)= 0.8xy - 0.64x^2 + y^2 - 0.8xy = y^2 - 0.64x^2 
    4. (b+0,5)^2= (b+0,5)(b+0,5) = b^2 + b + 0.25 
    5. (а-2х)^2= (а-2х)(а-2х) = a^2 - 2ax - 2ax +4x^2 = a^2 - 4ax +4x^2 
    6. (ab-1)^2 = (ab-1)(ab-1) = a^2 + ab + ab + b^2 -ab +1 = a^2 + b^2 + ab +1

    (2А+3)(2А-3)=4A^2-9

    (у-5б)(у+5б)=y^2-25B^2

    (0,8х+у)(у-0,8х)=-0.64X^2+Y^2

     (B+0.5)^2=B^2+B+0.25

     (а-2х)^2=A^2-4AX+4X^2

     (аб-1)^2=A^2B^2-2AB+1

  • Преобразуйте в многочлен:
    (2х-b)²;
    (b+3)(b-3)
    (5y-2х)(5у+2х)


    Решение: 1)4x²-4xb+b²
    2)b²-3b+3b-9=b²-9
    3)25y²+10xy-10xy-4x²=25y²-4x²

    Первое  преобразуется с помощью формулы сокращенного умножения $$ (a-b) ^{2} = a^{2}-2ab+b^{2} $$
    Тогда по формуле имеем: 
    $$ (2x-b)^{2}=(2x)^{2}-2*2x*b+b^{2} = 4 x^{2} -4xb+b^{2} $$
    2) это формула вот какая:$$ (a+b)(a-b)=a^{2}-b^{2} \\ (b+3)(b-3) =b^{2}-9 $$]
    3) по той же формуле :
    $$ (5y-2x)(5y+2x)=25y^{2}-4 x^{2} $$

  • 1) Преобразуйте в многочлен:
    -5(1-2c)^2=
    -4(3m+n)^2=
    2) Докажите что:
    a(a+b)+b(a+b)=(a+b)^2
    (a-b)^2=a(a-b)-b(a-b)
    Выделите квадрат двучлена: с^2+10
    x^2+3x-0.25
    Образец: x^2-8x+9=x^2-2*4*x+16-16+9=(x-4)^2-7


    Решение: $$ 1)\\ -5(1-2c)^2=-5(1-4c+4c^2)=-5+20c-20c^2\\ -4(3m+n)^2=-4(9m^2+6mn+n^2)=-36m^2-24mn-4n^2 \\ 2)\\ a(a+b)+b(a+b)=(a+b)(a+b)=(a+b)^2\\ (a+b)^2=(a+b)^2\\ \\(a-b)^2=a^2-2ab+b^2=a^2-ab-ab+b^2=\\ =(a^2-ab)-(ab-b^2)=a(a-b)-b(a-b)\\ a(a-b)-b(a-b)=a(a-b)-b(a-b) $$

    $$ 1)\ -5(1-2c)^2=-5(1-4c+4c^2)=-5+20c-20c^2 \\ -4(3m+n)^2=-4(9m^2+6mn+n^2)=-36m^2-24mn-4n^2 \\ \\ 2)\ a(a+b)+b(a+b)=(a+b)^2 \\ (a+b)(a+b)=(a+b)^2 \\ (a+b)^2=(a+b)^2 \\ \\ (a-b)^2=a(a-b)-b(a-b) \\ (a-b)^2=(a-b)(a-b) \\ (a-b)^2=(a-b)^2 \\ \\ 3)\ c^2+10=(c^2+2c*\frac{1}{2c}+\frac{1}{4c^2})-\frac{1}{4c^2}-1+10= \\ \\ =(c+\frac{1}{2c})^2+9-\frac{1}{4c^2} \\ \\ x^2+3x-0,25=(x^2+2x*1,5+2,25)-2,25-0,25= \\ \\ =(x+1,5)^2-2,5 $$

  • Преобразуйте в многочлен;
    1)(y-2)(y+3)-(y-1)²=
    2) 4(a+5)²-(4a²+40a)=


    Решение: y^2 -2y +3y -6 - (y^2 -2y +1) = y^2 +y - 6 - y^2 +2y - 1 = 3y - 7
    -
    4(a^2 + 10a +25) - 4a^2 - 40a = 4a^2 + 40a + 100 - 4a^2 - 40a = 100
     

    Надеюсь будет видно, если нет, то скажи

    y - y y - - y - y y y - - y y - y - - a a - a - a a a - a - a   Надеюсь будет видно если нет то скажи...

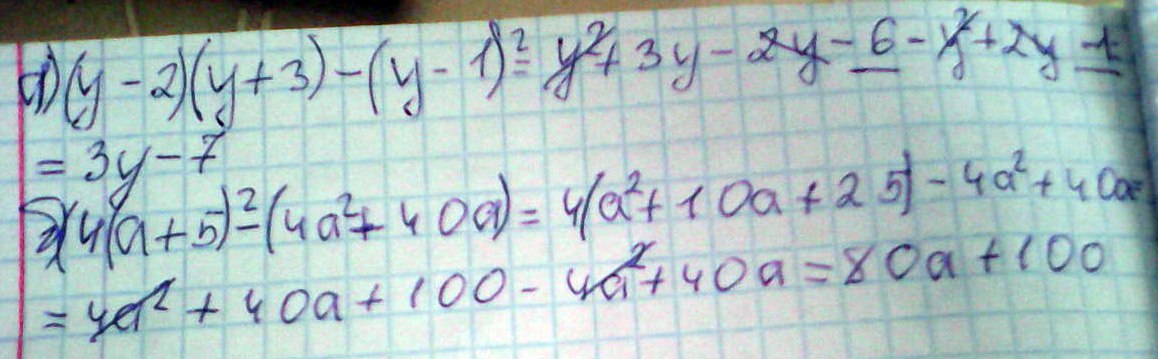
  • Преобразуйте в многочлен:
    а) 2(a-3)^2;
    б) 3(x+y)^2;
    в) -5(1-2c)^2;
    г) -4(3m+n)^2;
    д) 0,1(a+5)^2;
    e) -1/2(2u-v).


    Решение:

    Тут почти все на одну формулу (а+b)²=a²+2ab+b² или (а-b)²=a²-2ab+b²
    а) 2(a-3)^2=2(a²-6a+9)=2a²-12a+18;
    б) 3(x+y)^2=3(x²+2xy+y²)=3x²+6xy+3y²
    в) -5(1-2c)^2=-5(1-4c+4c²)=-5+20c-20c²=20c-20c²-5
     г) -4(3m+n)^2=4(9m²+6mn+n²)=36m²+24mn+4n²
    д) 0,1(a+5)^2=0,1(a²+10a+25)=0,1a²+a+2,5
    e) -1/2(2u-v)=-u+1/2v=1/2v-u

    Тут почти все на одну формулу а b a ab b или а-b a - ab b а a- a - a a - a б x y x xy y x xy y в - - c - - c c - c- c c- c -  г - m n m mn n m mn n д a a a a a e - u-v -u v v...
<< < 12 3 > >>