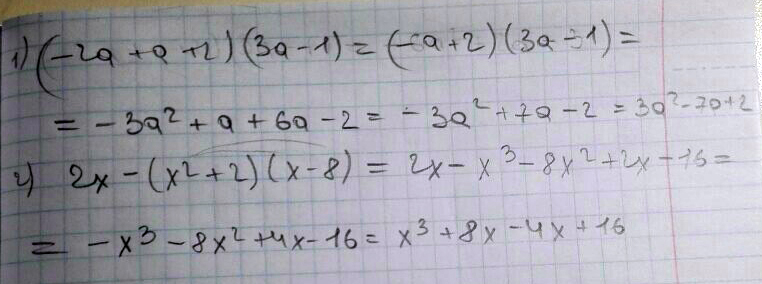преобразовать в многочлен
Преобразовать в многочлен (3x-5y)^2-3x(3x-10y) --------------(^)
Решение: (3x-5y)²-3x(3x-10y)=9x²-30xy+25y²-9x²+30xy=25y²Решение:(3x−5y)2−3x(3x−10y)
Возведение в степень:9x2−30xy+25y2−3x(3x−10y)
Раскрытие скобок:9x2−30xy+25y2−9x2+30xy=−30xy+25y2+30xy=
Приведение подобных:25y2
Ответ: 25y2Преобразование целых выражений
Вариант 1
1. Упростите выражение.
1) 5(а-2)^2+10a
2) (x-3)^2-(x^2+9)
2. Преобразуйте в многочлен.
1.(х-3)(х+3)-х(х-5)
2.(m-5)^2-(m-4)( m+4)
3. Найдите корень даного уравнения
(6а-1)(6а+1)=4а(9а+2)-1
-Вариант 2
1. Упростите выражение.
1)8(х-3)^2+16
2) (y-5)^2-(y+7)^2
2. Преобразуйте в многочлен.
1) (m-4)(m+4)+m(5-m)
2) (x-8)^2-(x-3)(x+3)
3. Найдите корень даного уравнения
(8x-1)(8x+1)=4x(16x+1)-2
________
Вариант А.
1 Разложите на множители.
а)2y^2-18
б) 2x^2-12x+18
2. Упростите выраежения.
а)(2а+3)(а-3)-2а(4+а)
б)(1-х)(х+1)+(х-1)^2
3. Докажите тождество
x^4-27x=(x^2-3x)(x^2+3x+9)
Вариант Б
1 Разложите на множители:а)64а-а^3
б) x^3-10x^2+25x
2. Упростите выражения:
а)(a+b)(a-2b)+(2b-a)(2b+a)
б)(3x+2)^2-(3x-1)^2
3. Докажите тождество
(x^2+3)^2=(x^2-3)(x^2+3)+6(x^2+3)
Решение: Преобразование целых выражений
Вариант 1
1. Упростите выражение.
1) 5(а-2)^2+10a=5(а^2-4а+4)+10а=5а^2-20а+20+10а=5а^2-10а+202) (x-3)^2-(x^2+9)=х^2-6x+9-x^2-9=-6x
2. Преобразуйте в многочлен.
1.(х-3)(х+3)-х(х-5)=x^2-9-x^2+5x=5x-9
2.(m-5)^2-(m-4)( m+4)=m^2-10m+25-m^2+16=-10m+41
3. Найдите корень даного уравнения
(6а-1)(6а+1)=4а(9а+2)-136a^2-1=36a^2+8a-1
36a^2-36a^2-8a=-1+1
-8a=0
a=0
-Вариант 2
1. Упростите выражение.
1)8(х-3)^2+16 =8(x^2-6x+9)+16=8x^2-48x+72+16=8x^2-48x+88
2) (y-5)^2-(y+7)^2=y^2-10y+25-y^2-14y-49=-24y-24=-24(y+1)
2. Преобразуйте в многочлен.
1) (m-4)(m+4)+m(5-m)=m^2-16+5m-m^2=5m-16
2) (x-8)^2-(x-3)(x+3)=x^2-16x+64-x^2+9=-16x+73
3. Найдите корень даного уравнения
(8x-1)(8x+1)=4x(16x+1)-264x^2-1=64x+4x-2
64x^2-64x^2-4x=-2+1
-4x=-1
x=1/4
_________________________________________________________________
Вариант А.
1 Разложите на множетели.
а)2y^2-18=2(y^2-9)=2(y-3)(y+3)
б) 2x^2-12x+18=2(x^2-6x+9)=2(x-3)^2=2(x-3)(x-3)
2. Упростите выраежения.
а)(2а+3)(а-3)-2а(4+а)=2a^2-6a+3a-9-8a-2a^2=-11a-9
б)(1-х)(х+1)+(х-1)^2=1-x^2+x^2-2x+1=2-2х=2(1-х)
3. Докажите тождество
x^4-27x=(x^2-3x)(x^2+3x+9)x(x^3-27)=x(x-3)(x^2+3x+9)
x(x^3-27)=x(x-3)(x^2+3x+9) тождество верно
Вариант Б
1 Разложите на множетели:
а)64а-а^3=a(64-a^2)=a(8-a)(8+a)
б) x^3-10x^2+25x=x(x^2-10x+25)=x(x-5)^2=x(x-5)(x-5)
2. Упростите выражения:
а)(a+b)(a-2b)+(2b-a)(2b+a)=a^2-2ab+ab-2b^2+4b^2-a^2=2b^2-ab
б)(3x+2)^2-(3x-1)^2=9x^2+12x+4-9x^2+6x-1=18x+3=3(6x+1)
3. Докажите тождество
(x^2+3)^2=(x^2-3)(x^2+3)+6(x^2+3)x^4+6x^2+9=x^4-9+6x^2+18
x^4+6x^2+9=x^4+6x^2+9 тождество верно
Преобразовать в многочлен произведение (-2a+a+2)(3a-1) и 2x-(x во второй степени +2)(x-8)
Решение:(-2*а+а+2)(3*а-1)=-6*а²+2*а+3*а²-а+6*а-2=-3*а²+7*а-2
2*х-(х²+2)(х-8)=2*х-(х³-8*х²+2*х-16)=2*х-х³+8*х²-2*х+16=-х³+8*х²+16
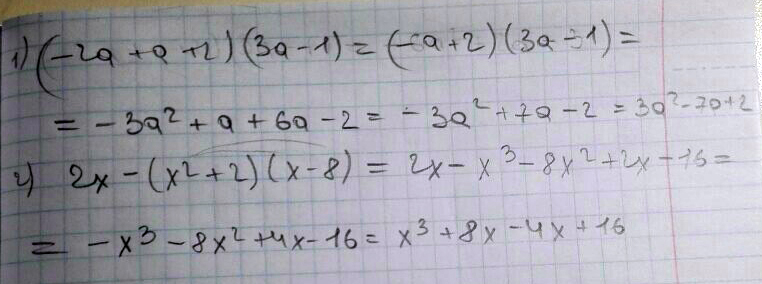
Разложить многочлен на множители: 6ах²-12ах³= ? 24a³с-3а²с= ? 5m²n-20mn²= ?
1-64b²= ?
Упростить выражение: (x-2)(x+4)-2x(1+x)= ? (2b-3)(3b+2)-3b(2b+3)=? Преобразовать в двучлен произведение: ( 2x²+y²)(y²-2x²)= ? (x-4y)(x+4y)= ?
Вычислить рациональным способом: 86²-14²= ? 15,9²-5,9²= ?
Решение: 1) 6ах²-12ах³=6ах²(1-2х)
2) 24а³с-3а²с=3а²с(8а-1)
3) 5m²n-20mn²=5mn(m-4n)
4) 1-64b²=(1-8b)(1+8b)
5) (x-2)(x-4)-2x(1+x)=x²-4x-2x+8-2x-2x²=-x²-8x+8
6) (2b-3)(3b+2)-3b(2b+3)=6b²-4b-9b-6-6b²-9b=-22b-6
7) (2x²+y²)(y²-2x²)=(y²+2x²)(y²-2x²)= $$ y^{4} -4 x^{4} $$
8) (x-4y)(x+4y)=x²-16y²
9) 86²-14²=(86-14)(86+14)=72*100=7200
10) 15,9²-5.9²=(15,9-5,9)(15,9+5,9)=10*21,8=218
Преобразование выражения в многочлен: (3а-а^2)^2-a^2(a-2)(a+2)+2a(7+3a^2) и 2x(x-3)-3x(x+5)
Решение: Расписываю подробно:
(3a-a^2)^2-a^2(a-2)(a+2)+2a(7+3a^2)=9a^2-6a^3+a^4-a^2*(a-2)*(a+2)+2a*(7+3a^2)=9a^2-6a^3+a^4-(a^3-a^2*2)*(a+2)+2a*(7+3a^2)=9a^2-6a^3+a^4-(a^4-a^2*4)+2a*(7+3a^2)=9a^2-6a^3+a^4-a^4+a^2*4+2a*(7+3a^2)=9a^2-6a^3+a^2*4+2a*(7+3a^2)=13a^2-6a^3+2a*(7+3a^2)=13a^2-6a^3+(14+6a^2)*a=13a^2-6a^3+14a+6a^3=13a^2+14a2x(x-3)-3x(x+5)=(2x-6)*x-3x*(x+5)=2x^2-6x-3x*(x+5)=2x^2-6x-(3x+15)*x=2x^2-6x-(3x^2+15x)=2x^2-6x-3x^2-15x=-x^2-6x-15x=-x^2-21x