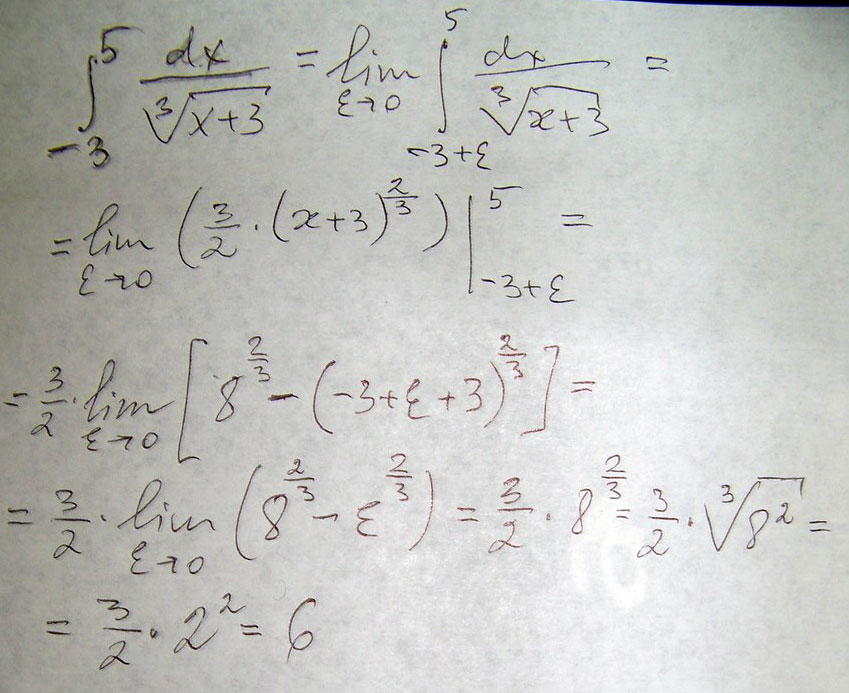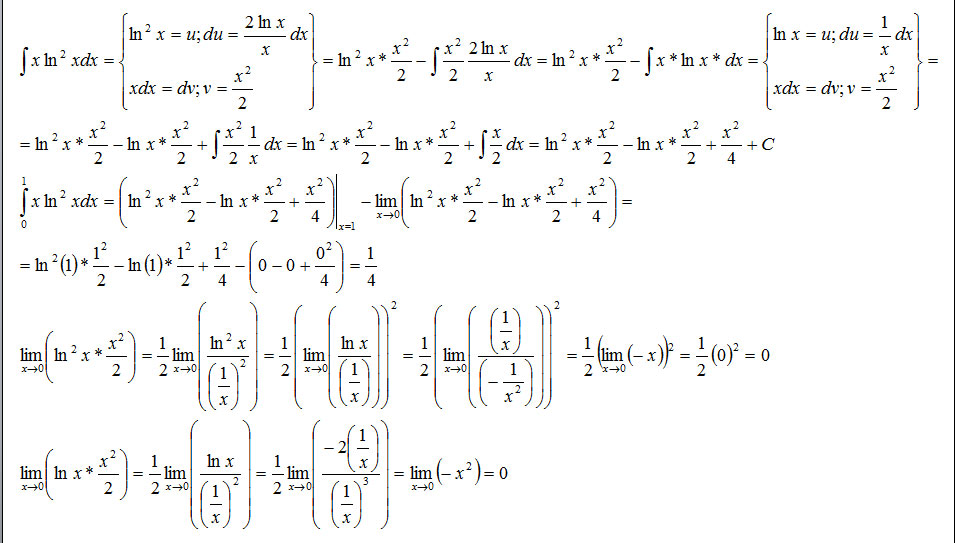интеграл »

несобственный интеграл

  • Вычислить несобственный интеграл или доказать его расходимость.
    \( \int\limits^5_3 { \frac{x}{ \sqrt[4]{x^{2}-9 } } }, dx \)


    Решение: $$ \int\limits^5_3 { \frac{x}{ \sqrt[4]{ x^2-9}} } \, dx $$
    Найдем соответствующий неопределенный интеграл:
    $$ J(x) = \int\frac{x}{ \sqrt[4]{ x^2-9}}\, dx $$
    Сделаем замену $$ x = 3cht $$, тогда
    $$ \sqrt[4]{x^2-9} = \sqrt[4]{9ch^2t-9} = \sqrt[4]{9sh^2t} = \sqrt{3sht} \\ dx = 3sht $$.
    Подставим в интеграл:
    $$ J(x) = \int\frac{x}{ \sqrt[4]{ x^2-9}} \, dx = \int{ \frac{9shtcht}{ \sqrt{3sht}} } \, dt = 3\sqrt{3}\int{cht\sqrt{sht}} \, dt = 3\sqrt{3}\int{\sqrt{sht}} \,d(sht) = \\ 3 \sqrt{3} \frac{sh^ \frac{3}{2} t}{ \frac{3}{2} } = 2\sqrt{3}(ch^2t-1)^\frac{3}{4}+C $$.
    Делаем обратную замену:
    $$ J(x) = 2\sqrt{3}( \frac{x^2}{9} -1)^\frac{3}{4}+C = \frac{2\sqrt{3}( x^2 -9)^\frac{3}{4}}{9^\frac{3}{4}} + C= \frac{2\sqrt{3}( x^2 -9)^\frac{3}{4}}{3\sqrt{3}} + C = \ \frac{2}{3} (x^2-9)^ \frac{3}{4} + C $$.
    Возьмем значение произвольной постоянной $$ C = 0 $$.
    Наконец, воспользуемся формулой Ньютона-Лейбница:
    $$ \int\limits^5_3 { \frac{x}{ \sqrt[4]{ x^2-9}} } \, dx = J(5) - J(3) = \frac{2}{3} * 16^ \frac{3}{4} = \frac{16}{3} $$.

  • Несобственный интеграл от (- бесконечности) до (0)

    x*(e^x)*dx


    Решение: =предел при b стремящемся к -бесконечности от интегрла от b до 0  (x*e^x) dx

    найдем интеграл:

    интеграл от b до 0 (x*e^x)dx = интеграл от b до 0 (x) d(e^x) = x*e^x|(от b до 0) -

    - интеграл от b до 0 (e^x) dx = -b*e^b - e^x|(от b до 0) = -b*e^b -1 +e^b

    Теперь от этого выражения вычисляем предел при b стремящемся к -бесконечности

    Расписываем на сумму пределов и получаем: 0-1+0 = -1

    Ответ: -1

  • Вычислить несобственный интеграл или установить его расходимость \(\int\limits^{5}_{-3} \frac{dx}{\sqrt[3]{x + 3}} \)


    Решение: $$ \int\limits^{5}_{-3} \frac{dx}{\sqrt[3]{x + 3}} = \lim\limits_{\varepsilon \to -3}{\int\limits^{5}_{\varepsilon} \frac{dx}{\sqrt[3]{x + 3}}} =\lim\limits_{\varepsilon \to -3} \frac{3}{2}\sqrt[3]{(x + 3)^2} |^{5}_{\varepsilon} = \\ \frac{3}{2} \lim\limits_{\varepsilon \to -3} \sqrt[3]{(8)^2} - \underbrace{\sqrt[3]{(\varepsilon + 3)^2}}\limits_{\to 0} = \frac{3}{2} \lim\limits_{\varepsilon \to -3} \sqrt[3]{64} = \frac{3}{2}*4 = 6 $$

    Решение примера во вложениях : 

     

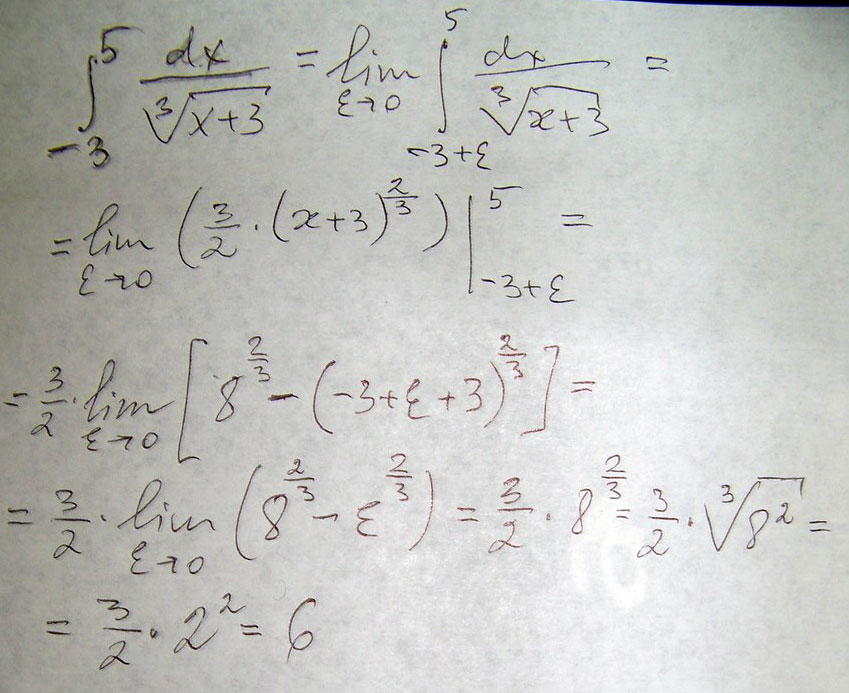
    int limits - frac dx sqrt x lim limits varepsilon to - int limits varepsilon frac dx sqrt x lim limits varepsilon to - frac sqrt x varepsilon frac lim limits varepsilon to -...

  • Вычислить несобственный интеграл или доказать расходимость. \( \int\limits^{-3}_{-\infty } {\frac{x\, dx}{(x^2+1)^2}} \, dx \)


    Решение: $$ \int\limits^{-3}_{-\infty } {\frac{x\, dx}{(x^2+1)^2}} \, dx =\lim\limits _{A\to -\infty }\int _{A}^{-3}\frac{x\, dx}{(x^2+1)^2}=\\\\=[\, \int \frac{x\, dx}{(x^2+1)^2}=[\, t=x^2+1,dt=2x\, dx,\; \; \frac{1}{2}\int t^{-2}dt=\\\\=\frac{1}{2}\cdot \frac{t^{-1}}{-1}=-\frac{1}{2t}\, ]=\lim\limits _{A\to \infty }(-\frac{1}{2}\cdot \frac{1}{x^2+1})|_{A}^{-3}=\\\\=-\frac{1}{2}\lim\limits _{A\to \infty }(\frac{1}{10}-\frac{1}{A^2+1})=-\frac{1}{2}(\frac{1}{10}-0)=-\frac{1}{20}\; \to \; \; sxoditsya $$

    $$ \int\limits^{-3}_{-\infty} { \frac{xdx}{(x^2+1)^2} }=|t=x^2+1; dt=2xdx|=\\=\frac{1}{2}*\int\limits^{10}_{\infty} { \frac{dt}{t^2} }=\lim_{n \to \infty}(-\frac{1}{2t}|^{10}_{n})=\lim_{n \to \infty}(-\frac{1}{20}+ \frac{1}{2n} )=-\frac{1}{20} $$

  • Вычислите несобственный интеграл или докажите его расходимость \( \int\limits^{\infty }_1 {\frac{4}{x(ln^2x+1)}} \, dx \)


    Решение: $$ \int\limits^{\infty }_1 {\frac{4}{x(ln^2x+1)}} \, dx =\lim\limits _{A\to +\infty }\int _1^{A}\, \frac{4\, dx}{x(ln^2x+1)}=\\\\=[\, t=lnx,\; dt= \frac{dt}{t},\; \int \frac{dt}{t^2+1}=arctgt+C\, ]=\\\\= \lim\limits _{A \to +\infty} \, \int _1^{A} \, \frac{4\cdot d(lnx)}{ln^2x+1} =\lim\limits _{x\to +\infty }\, (4arctg(lnx))|_1^{A}=\\\\= \lim\limits _{A \to +\infty} \, (4arctg(lnA)-4arctg1)=[\, +\infty -4\cdot \frac{\pi}{4}\, ]=+\infty \\\\integral\; \; rasxoditsya $$
    P.S. Так как у log не указано основание, то считаем, что это натуральный логарифм, который обозначается ln x.

  • Нужно решить подробно несобственный интеграл второго рода.\( \int\limits {xln ^{2}x } \, dx \)


    Решение: 1)u=ln²x⇒du=2lnxdx/x U dv=xdx⇒v=x²/2
    $$ \int\limits {xln ^{2}x } \, dx =ln ^{2}x*x^2/2 - \int\limits {xlnx} \, dx $$
    2)u=lnx⇒du=dx/x U dv=xdx⇒v=x²/2
    $$ \int\limits {xlnx} \, dx =lnx*x^2/2- 1/2\int\limits {x} \, dx =lnx*x^2/2 -x^2/4 \\ \int\limits^1_0 {xln ^{2}x } \, dx =x^2ln ^{2} x/2-x^2lnx/2+x^2/4|(1-0)=1/4 $$

    ************************

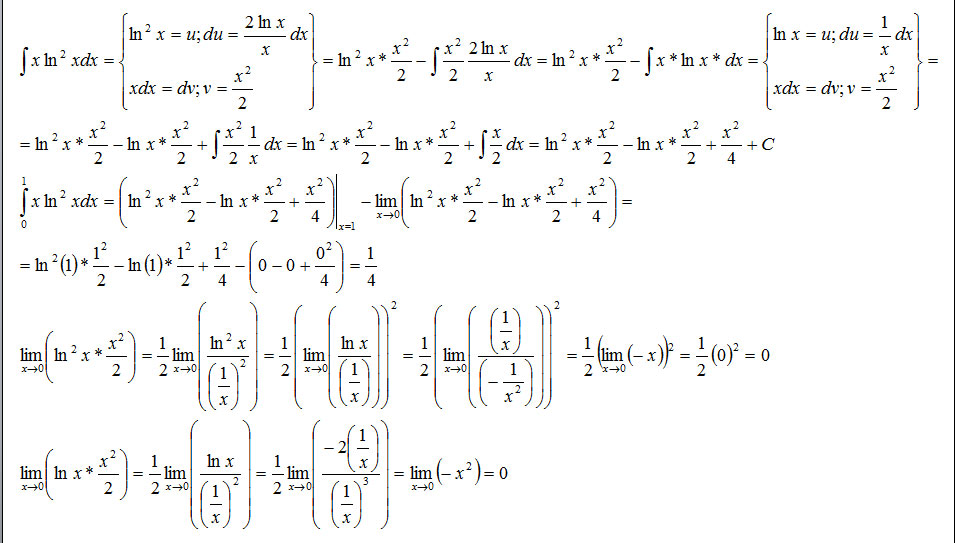
    u ln x du lnxdx x U dv xdx v x int limits xln x dx ln x x - int limits xlnx dx u lnx du dx x U dv xdx v x int limits xlnx dx lnx x - int limits x dx lnx x -x int limits xln x...

  • Вычислить несобственный интеграл или указать его расходимость: \( \int\limits_{0}^{+\infty} \dfrac{x}{\sqrt{x^2+1}}dx \)


    Решение: $$ \int\limits_{0}^{+\infty} \dfrac{x}{\sqrt{x^2+1}}dx=2\int\limits_{0}^{+\infty} \dfrac{d(x^2+1)}{\sqrt{x^2+1}}=4\int\limits_{0}^{+\infty} d(\sqrt{x^2+1})=\\\\ =4[\sqrt{x^2+1}]_{0}^{+\infty}=4lim_{a\to +\infty}[\sqrt{x^2+1}]_{0}^{a}=\\\\ =4lim_{a\to +\infty}(\sqrt{a^2+1}-1)=+\infty $$
    Значит, несобственный интеграл расходится.

    Вычислим сначала неопределенный интеграл
    интегр(x/(x^2+1)^(1/2))dx=(1/2) интегр(1/(x^2+1)^(1/2))d(x^2+1)=
    =(1/2) интеграл(x^2+1)^(-1/2)d(x^2+1) =(1/2)*2(x^2+1)^(1/2)+C =(x^2+1)^(1/2)+C
    Теперь найдем несобственный интеграл
    интегралI от 0 до +бесконI(x/(x^2+1))dx =
    =limIa-> бескоенI(интегралI от 0 до aI(x/(x^2+1))dx)
    =limIa-> бесконI((x^2+1)^(1/2)Iот 0 до аI) =
    =limIa-> бесконI((a^2+1)^(1/2)-1)=бесконечн.
    Следовательно интеграл расходится 

  • Нужно исследовать на сходимость несобственный интеграл. \( \int _{-2}^0\, \frac{dx}{x^2+2x+10} \)


    Решение: Интеграл не является несобственным интегралом 1 рода, так как нет бесконечных пределов интегрирования.
    Интеграл не является несобственным интегралом 2 рода, т. к. на промежутке [ -2,0 ] он определён и нет точек разрыва.
     $$ x^2+2x+10>0,\; t.k.\; \; D=4-40<0\; \; \to \; \; x^2+2x+10e 0 $$.
    $$ \int _{-2}^0\, \frac{dx}{x^2+2x+10}=\int _{-2}^0\, \frac{dx}{(x+1)^2+9} =arctg\frac{x+1}{3}\, |_{-2}^0=\\\\=arctg\frac{1}{3}-arctg(-\frac{1}{3})=2arctg\frac{1}{3} $$

  • Вычислить несобственные интегралы 1) ∫cos3x/(1-sin3x)^5/6
    2) ∫xdx/√(16x^4-1)


    Решение: 1) ∫cos3x/(1-sin3x)^5/6
    введем замену 1-sin3x = t
    тогда dt = (1-sin3x)’dx
    dt = -cos3xdx
    cos3xdx = -dt
    Получается ∫-dt/t^(5/6) = -6*t^(1/6)
    введем обратную замену
    -6*(1-sin3x)^1/6
    при x = π/6, 3x = π/2, sin(π/2) = 1 => -6*(1-1) = 0
    x = 0, 3x=0, sin(0)= 0 => -6*(1-0)  = -6
    интеграл равен 0 -6 = 6
    2) ∫xdx/√(16x^4-1)
    введем замену t = 4x^2 => dt = 8xdx =>xdx = dt/8
    Тогда получаем
    1/8∫dt/√(t^2-1) = 1/8 * arch(t)
    введем обратную замену
    1/8 * arch(4x^2 -1)

  • вычислить несобственные интегралы \(1)\quad \int\limits^{\infty }_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx\\ 2)\quad \int\limits^4_2 {\frac{x\, dx}{\sqrt{x^2-4}}} \)


    Решение: $$ 1)\quad \int\limits^{\infty }_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx =\lim\limits _{A\to +\infty } \int\limits^{A}_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx =\lim\limits _{A\to +\infty } \int\limits^{A}_1 {e^{\frac{1}{x}}} \, d(-\frac{1}{x}) =\\\\=\lim\limits _{A\to +\infty }(-e^{\frac{1}{x}})|_1^{A}=\lim\limits _{A\to +\infty }(-e^{\frac{1}{A}}+e)=-e^0+e=e-1\\\\2)\quad \int\limits^4_2 {\frac{x\, dx}{\sqrt{x^2-4}}} =\lim\limits _{\varepsilon \to 0} \int\limits^4_{2+\varepsilon } {\frac{2x\, dx}{2\sqrt{x^2-4}} }= \\ =\lim\limits _{\varepsilon \to 0}\, (\frac{1}{2}\cdot 2\sqrt{x^2-4})|_{2+\varepsilon }^4=\lim\limits _{\varepsilon \to 0}\, (\sqrt{16-4}-\sqrt{4\varepsilon +\varepsilon ^2})=\sqrt{12} $$

1 2 > >>