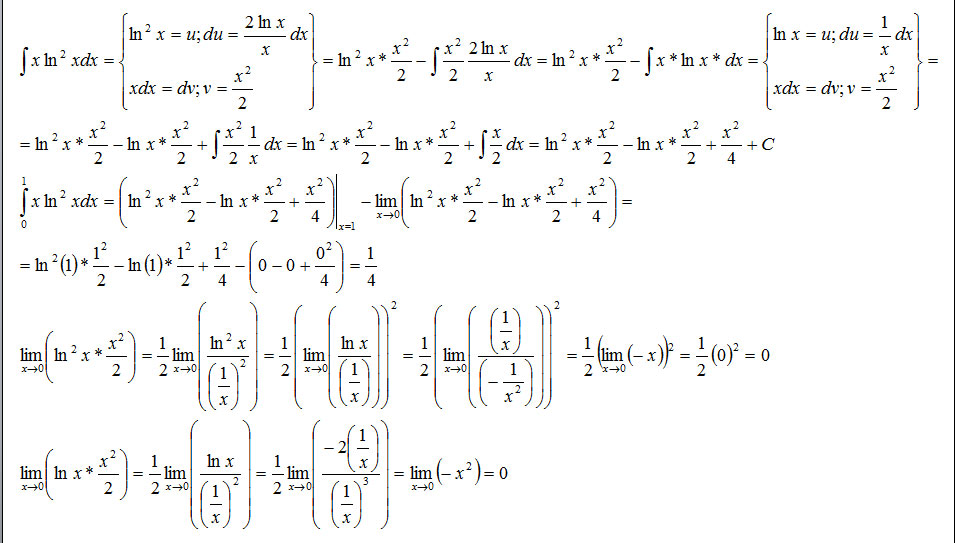интеграл »

несобственный интеграл - страница 2

  • Нужно решить подробно несобственный интеграл второго рода.\( \int\limits {xln ^{2}x } \, dx \)


    Решение: 1)u=ln²x⇒du=2lnxdx/x U dv=xdx⇒v=x²/2
    $$ \int\limits {xln ^{2}x } \, dx =ln ^{2}x*x^2/2 - \int\limits {xlnx} \, dx $$
    2)u=lnx⇒du=dx/x U dv=xdx⇒v=x²/2
    $$ \int\limits {xlnx} \, dx =lnx*x^2/2- 1/2\int\limits {x} \, dx =lnx*x^2/2 -x^2/4 \\ \int\limits^1_0 {xln ^{2}x } \, dx =x^2ln ^{2} x/2-x^2lnx/2+x^2/4|(1-0)=1/4 $$

    ************************

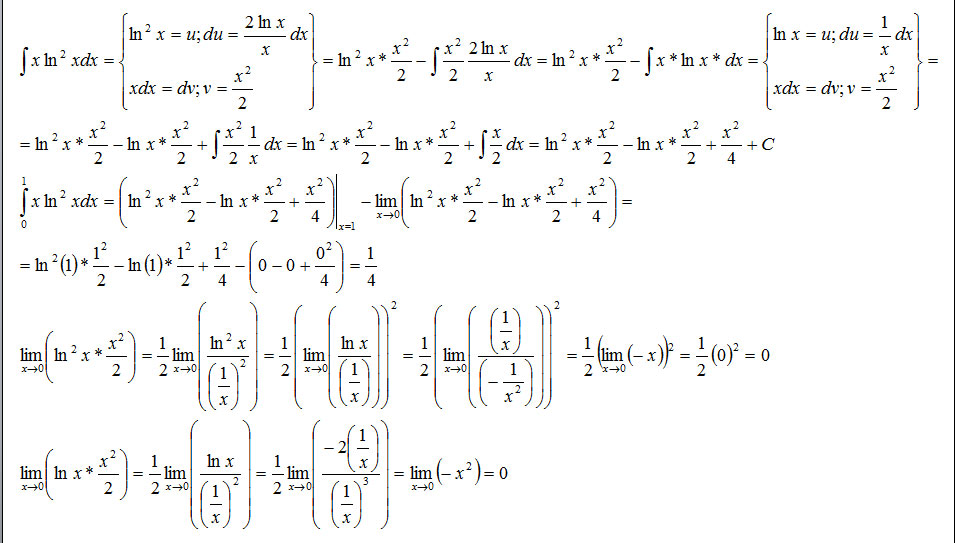
    u ln x du lnxdx x U dv xdx v x int limits xln x dx ln x x - int limits xlnx dx u lnx du dx x U dv xdx v x int limits xlnx dx lnx x - int limits x dx lnx x -x int limits xln x...

  • Вычислить несобственный интеграл или указать его расходимость: \( \int\limits_{0}^{+\infty} \dfrac{x}{\sqrt{x^2+1}}dx \)


    Решение: $$ \int\limits_{0}^{+\infty} \dfrac{x}{\sqrt{x^2+1}}dx=2\int\limits_{0}^{+\infty} \dfrac{d(x^2+1)}{\sqrt{x^2+1}}=4\int\limits_{0}^{+\infty} d(\sqrt{x^2+1})=\\\\ =4[\sqrt{x^2+1}]_{0}^{+\infty}=4lim_{a\to +\infty}[\sqrt{x^2+1}]_{0}^{a}=\\\\ =4lim_{a\to +\infty}(\sqrt{a^2+1}-1)=+\infty $$
    Значит, несобственный интеграл расходится.

    Вычислим сначала неопределенный интеграл
    интегр(x/(x^2+1)^(1/2))dx=(1/2) интегр(1/(x^2+1)^(1/2))d(x^2+1)=
    =(1/2) интеграл(x^2+1)^(-1/2)d(x^2+1) =(1/2)*2(x^2+1)^(1/2)+C =(x^2+1)^(1/2)+C
    Теперь найдем несобственный интеграл
    интегралI от 0 до +бесконI(x/(x^2+1))dx =
    =limIa-> бескоенI(интегралI от 0 до aI(x/(x^2+1))dx)
    =limIa-> бесконI((x^2+1)^(1/2)Iот 0 до аI) =
    =limIa-> бесконI((a^2+1)^(1/2)-1)=бесконечн.
    Следовательно интеграл расходится 

  • Нужно исследовать на сходимость несобственный интеграл. \( \int _{-2}^0\, \frac{dx}{x^2+2x+10} \)


    Решение: Интеграл не является несобственным интегралом 1 рода, так как нет бесконечных пределов интегрирования.
    Интеграл не является несобственным интегралом 2 рода, т. к. на промежутке [ -2,0 ] он определён и нет точек разрыва.
     $$ x^2+2x+10>0,\; t.k.\; \; D=4-40<0\; \; \to \; \; x^2+2x+10e 0 $$.
    $$ \int _{-2}^0\, \frac{dx}{x^2+2x+10}=\int _{-2}^0\, \frac{dx}{(x+1)^2+9} =arctg\frac{x+1}{3}\, |_{-2}^0=\\\\=arctg\frac{1}{3}-arctg(-\frac{1}{3})=2arctg\frac{1}{3} $$

  • Вычислить несобственные интегралы 1) ∫cos3x/(1-sin3x)^5/6
    2) ∫xdx/√(16x^4-1)


    Решение: 1) ∫cos3x/(1-sin3x)^5/6
    введем замену 1-sin3x = t
    тогда dt = (1-sin3x)’dx
    dt = -cos3xdx
    cos3xdx = -dt
    Получается ∫-dt/t^(5/6) = -6*t^(1/6)
    введем обратную замену
    -6*(1-sin3x)^1/6
    при x = π/6, 3x = π/2, sin(π/2) = 1 => -6*(1-1) = 0
    x = 0, 3x=0, sin(0)= 0 => -6*(1-0)  = -6
    интеграл равен 0 -6 = 6
    2) ∫xdx/√(16x^4-1)
    введем замену t = 4x^2 => dt = 8xdx =>xdx = dt/8
    Тогда получаем
    1/8∫dt/√(t^2-1) = 1/8 * arch(t)
    введем обратную замену
    1/8 * arch(4x^2 -1)

  • вычислить несобственные интегралы \(1)\quad \int\limits^{\infty }_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx\\ 2)\quad \int\limits^4_2 {\frac{x\, dx}{\sqrt{x^2-4}}} \)


    Решение: $$ 1)\quad \int\limits^{\infty }_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx =\lim\limits _{A\to +\infty } \int\limits^{A}_1 \frac{e^{\frac{1}{x}}}{x^2} \, dx =\lim\limits _{A\to +\infty } \int\limits^{A}_1 {e^{\frac{1}{x}}} \, d(-\frac{1}{x}) =\\\\=\lim\limits _{A\to +\infty }(-e^{\frac{1}{x}})|_1^{A}=\lim\limits _{A\to +\infty }(-e^{\frac{1}{A}}+e)=-e^0+e=e-1\\\\2)\quad \int\limits^4_2 {\frac{x\, dx}{\sqrt{x^2-4}}} =\lim\limits _{\varepsilon \to 0} \int\limits^4_{2+\varepsilon } {\frac{2x\, dx}{2\sqrt{x^2-4}} }= \\ =\lim\limits _{\varepsilon \to 0}\, (\frac{1}{2}\cdot 2\sqrt{x^2-4})|_{2+\varepsilon }^4=\lim\limits _{\varepsilon \to 0}\, (\sqrt{16-4}-\sqrt{4\varepsilon +\varepsilon ^2})=\sqrt{12} $$

<< < 12 3 > >>