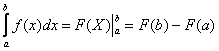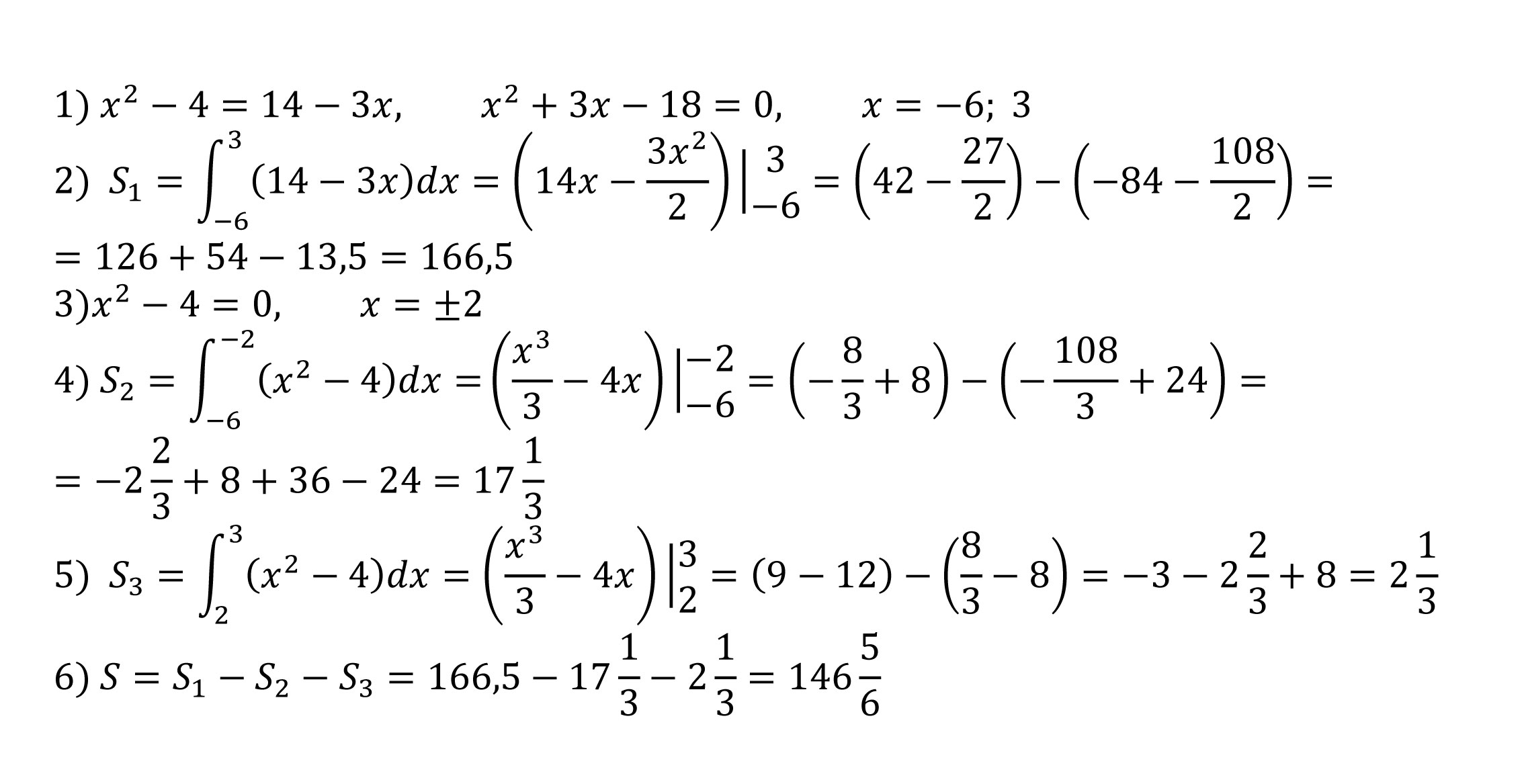интеграл »

площадь с помощью интеграла

  • Найти площадь криволинейной трапеции с помощью интеграла:

    у = х^2 - 1 у=3

    у = 4х-х^2 у=х у=0


    Решение: $$ f(x)_1=y=x^{2}-1, f(x)_2=y =3 $$

    Находим первообразные:

    $$ F(x)_1=\frac{x^{3}}{3}-x+C \\ F(x)_2=3x+C $$

    Находим ограничения трапеции, путем приравнивания ф-ий.

    $$ f(x)=y=x^{2}-1=3 \\ x^{2}=4 \\ x_1=2,\ x_2=-2 $$

    Получается интегрирования ф-ии ограничено $$ xe[-2;2] \\ S=\int\limits^2_2 {F_1(x)-F_2(x)} \, dx =\int\limits^2_2 {\frac{6x-x^{3}}{3}} \, dx =\frac{12-8}{3}-\frac{-12+8}{3}=\frac{8}{3} $$ (в интеграле внизу -2, просто чего-т не рисуется)

    Ответ: $$ S=\frac{8}{3} $$

  • C помощью определённого интеграла найти площадь фигуры ограниченной следующими линиями y=0 y=3x x=1 x=3


    Решение: $$ S= \int\limits^3_1 {3x} \, dx = \dfrac{3x^2}{2} \big|_1^3= \dfrac{3\cdot 3^2}{2}- \dfrac{3\cdot 1^2}{2}=12 $$

    Ищем интергал на отрезке от 1 до 3.  Первообразная равна 3x^2/2. Считаем по формуле. Получаем 25/2=12,5

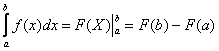
    S int limits x dx dfrac x big dfrac cdot - dfrac cdot Ищем интергал на отрезке от до .  Первообразная равна x . Считаем по формуле. Получаем...

  • Найти площадь фигуры, ограниченной линиями: y=x^2-4 ; y=14-3x; y=0. с помощью опр. интеграла


    Решение: 1) Найдем абсциссы точек пересеения параболы и прямой

    2) Найдем площадь фигуры ограниченной прямой и осью ОХ

    3) Найдем абсциссы точек пересечения параболы с ОХ

    4) Найдем площадь левой фигуры, ограниченной параболой от х = - 6 до х = - 2

    5) Найдем площадь фигуры справа, ограниченной параболой от х = 2 до х = 3 

    6) Найдем искомую площадь, ограниченную прямой, параболой и осью ОХ

    Это алгоритм. . 

     

    S=S₁-S₂-S₃+S₄, где S₁ и S₃ - площадь под прямой; S₂ и S₄ - площадь под параболой 

      x₄  x₃ x₄ x₁

    S=∫ (14-3x)dx - ( ∫ (x²-4)dx + ∫ (14-3x)dx) + ∫ (x²-4)dx

      x₁ x₂ x₃ x₂

    x₁ - ордината пересечения прямой y= 14-3x с осью Оy или прямой y=0

    x₂ - ордината пересечения параболы с осью Оx

    x₃ - ордината пересечения прямой y= 14-3x с параболой

    x₄ - ордината пересечения прямой y= 14-3x с осью Оx

    1) x₁=0

    2)14-3x₄=0

      x₄=14/3

    3) x₂²-4=0

      x₂=±2 - нам нужно x₂=2

    4) x₃²-4=14-3x₃

      x₃²+3x₃-18=0

      D=81, x₃=-6 и x₃=3 - нам нужно x₃=3

      14/3 3 14/3 0 14/3 3 14/3

    S=∫ (14-3x)dx - ∫ (x²-4)dx - ∫ (14-3x)dx + ∫ (x²-4)dx = 14x-3/2*x² | - 1/3*x³-4x | - 14x-3/2*x² | +

      0 2 3 2 0 2 3

      0

    +1/3*x³-4x | = 98/3 - 7/3 - 25/6 + 16/3 = 189/6  = 31,5

      2

     Ответ: 31,5

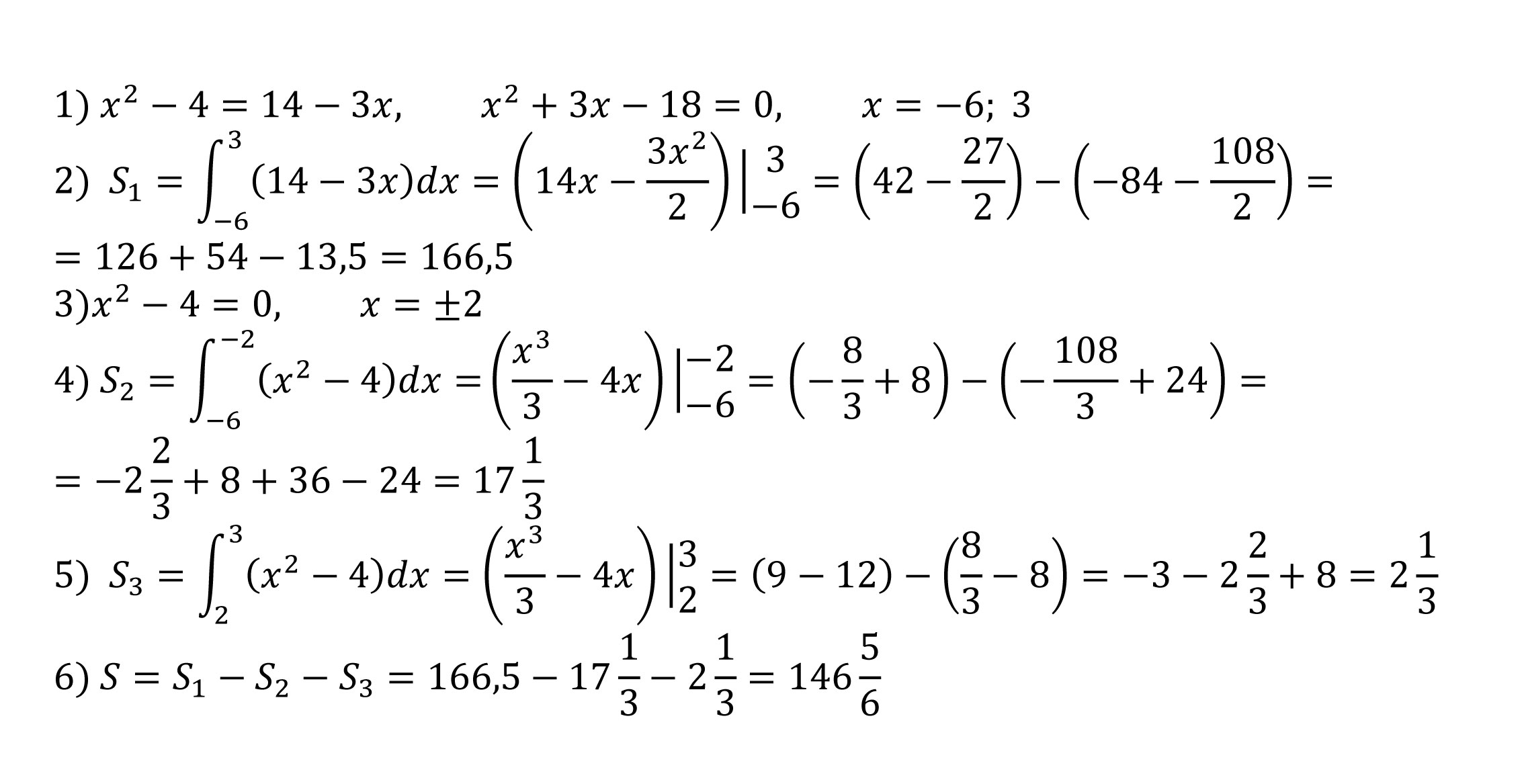
    Найдем абсциссы точек пересеения параболы и прямой Найдем площадь фигуры ограниченной прямой и осью ОХ Найдем абсциссы точек пересечения параболы с ОХ Найдем площадь левой фи...

  • Найти с помощью определённого интеграла площадь плоской фигуры, расположенной в первом квадранте и ограниченной параболой y=4x^2, прямой y=-2x+6 и осью OX


    Решение: Пересечения прямой и параболы 4x²=-2x+6 4x²+2x-6=0
    D=4+96 √D=10 x1=1/8[-2-10]=-12/8 =-1.5
    x2=1/8[-2+10]=1 поскольку условие требует только 1-го квадранта, то
    получаем х лежит в границах 0 до 1.
    площадь проще всего получить складывая площадь внутри параболы с площадью треугольника с катетами 1 и 2 (это 6-4=2), 6 значение -2х+6
    при х=0.
    площадь параболы s=∫4x²dx=4x³/3 от 0 до 1=4/3
    треугольника 0,5*1*2=1
    искомая площадь 4/3+1=2 1/3

  • Найти площадь криволинейной трапеции с помощью определенного интеграла, ограниченную линиями: \( y=\sqrt{2x-1} \, y=0 \, x=5 \)


    Решение: $$ y=\sqrt{2x-1} $$ - это верхняя ветвь параболы с вершиной в точке(1/2, 0), ветви направлены вправо (ось симметрии параболы - ось ОХ)
    Поэтому пределы изменения х- от 1/2 до 5.
    $$ S=\int_{1/2}^5\sqrt{2x-1}dx=\frac{1}{2}\cdot \frac{2}{3}\cdot(2x-1)^{\frac{3}{2}}|_{1/2}^5=\\=\frac{1}{3}((3-1)^{\frac{3}{2}}-(10-1)^{\frac{3}{2}}=\frac{1}{3}(2^{\frac{3}{2}}-3^3)=\frac{1}{3}(2\sqrt2-9)=\frac{2}{3}\sqrt2-3 $$

1 2 > >>