модуль »
модуль числа, противоположные числа
Про число известно, что: оно больше (-15) и меньше 3; число, ему противоположное, больше 8 и меньше 12; модуль этого числа-число нечётное; расстояние от точки, соответствующей этому числу на числовой оси, до начала отсчёта больше 10. Найдите это число
Решение: -15 < x < 3
8 < -x < 12, умножаем второе двойное неравенство на (-1), меняем знаки, получаем, что -12 < x < -8/ Значит, интервал, которому принадлежит х имеет вид (-12; -8) и этот интервал удовлетворяет так же и первому двойному неравенству. Числа из этого интервала: -11,10,9. Последнему условию про модуль удовлетворяют только 2 числа: 11 и 9.найдите все целые числа модуль которых больше 1 но меньше 3?
Решение: Преобразуем текст, в математический язык: 1<|x|<3Теперь, запишем в виде системы(для удобства)
{|x|>1 (1)
{|x|<3 (2)
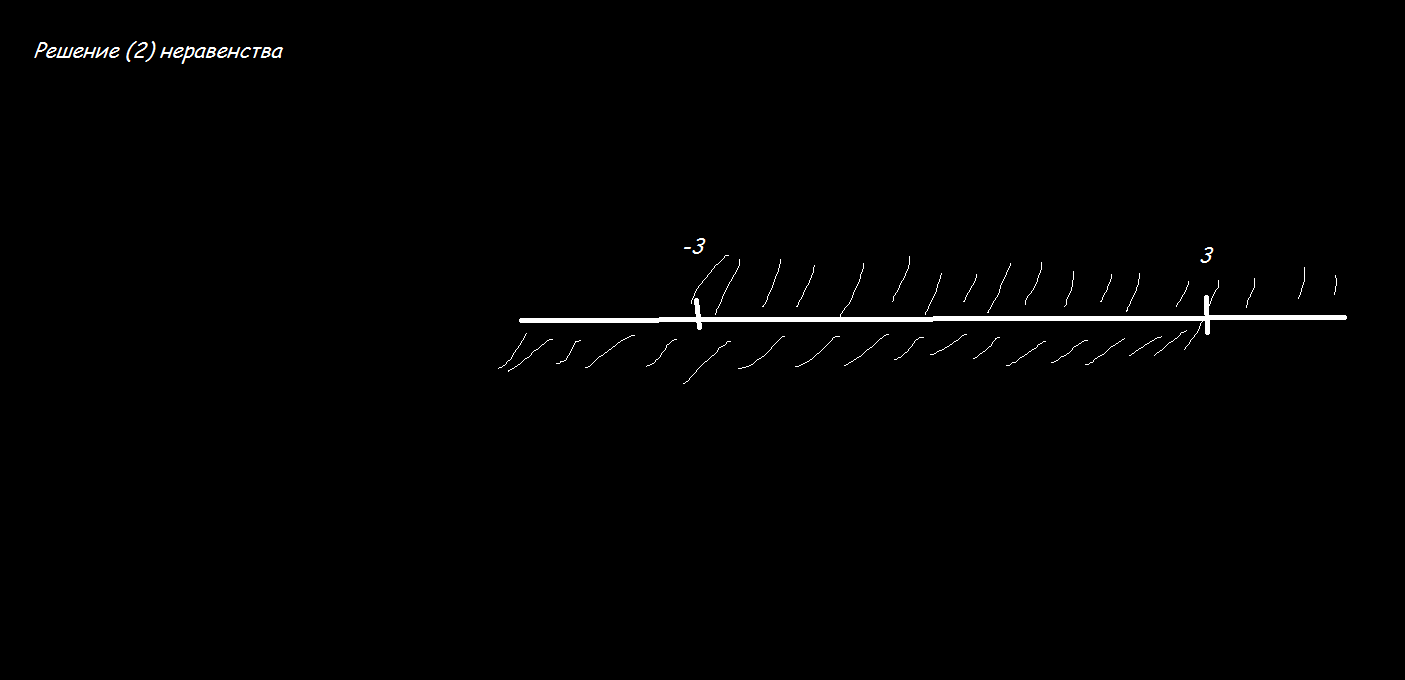
Решим (1) неравенство, раскрывая модуль получим решения на промежутке(см. вложения)
Решим (2) неравенство, раскрывая модуль, получим решения на промежутке(см. вложения)
Объеденим, два решения, и отберем все целые числа(см. вложения)
Ответ: 2,2.
-2 и 2.
1) приведите примеры чисел при которых модуль которых равен 12, больше 12, меньше 12
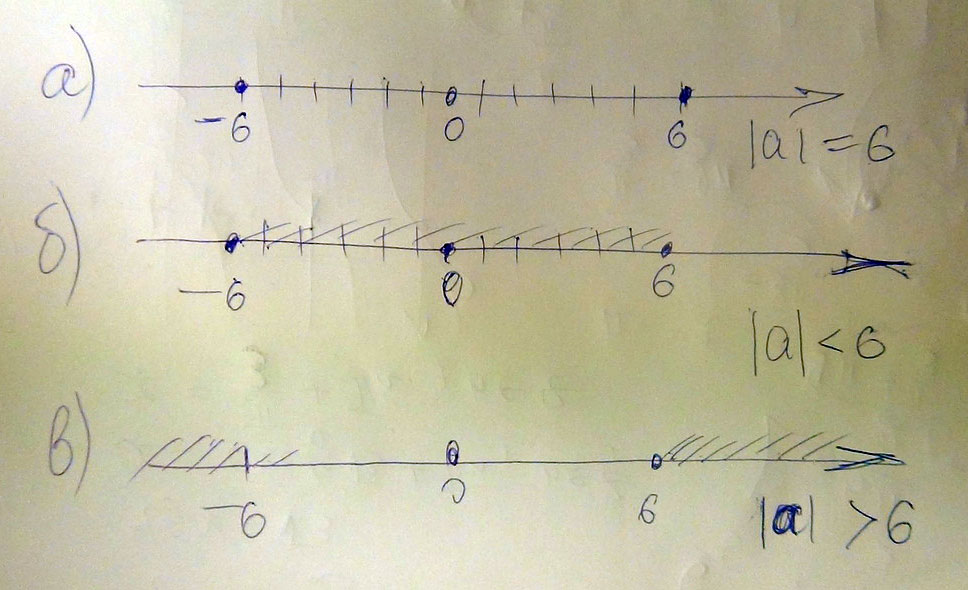
2) пусть а это некоторое число. покажите на координтной прямой где могут разпологаться точки изображающие это число если известно сто а) \а\=6 б) \а\меньше 6 в) \а\а больше 6
Решение: 1) Числа, модуль которых равен 12: 12; -12
Числа, модуль которых больше 12: 13; -13; 14; -14; 15,15 и т. д.
Числа модуль которых меньше 12: 11; -11; 10; -10; 9; -9 и т. д.
2) а) Если | a | = 6, то числа лежат на расстоянии 6 ед. от нуля слева и справа
б) Если | a | < 6, то числа расположены между числами -6 и 6
в) Если | a | > 6, то числа расположены левее от -6 и правее 6
см. на прикрепленном файле
Какое число на 12,5% меньше, чем сумма чисел 6V32 и 4V72?»
V-это модуль
Решение: 6√32+4√72=6√16*2+4√36*2=24√2+24√2=2(24√2)=48√2
100 - 12,5=87,5%
48√2 - 100%
x - 87,5%
(48√2/100)*87,5=0,48√2*87,5=42√2
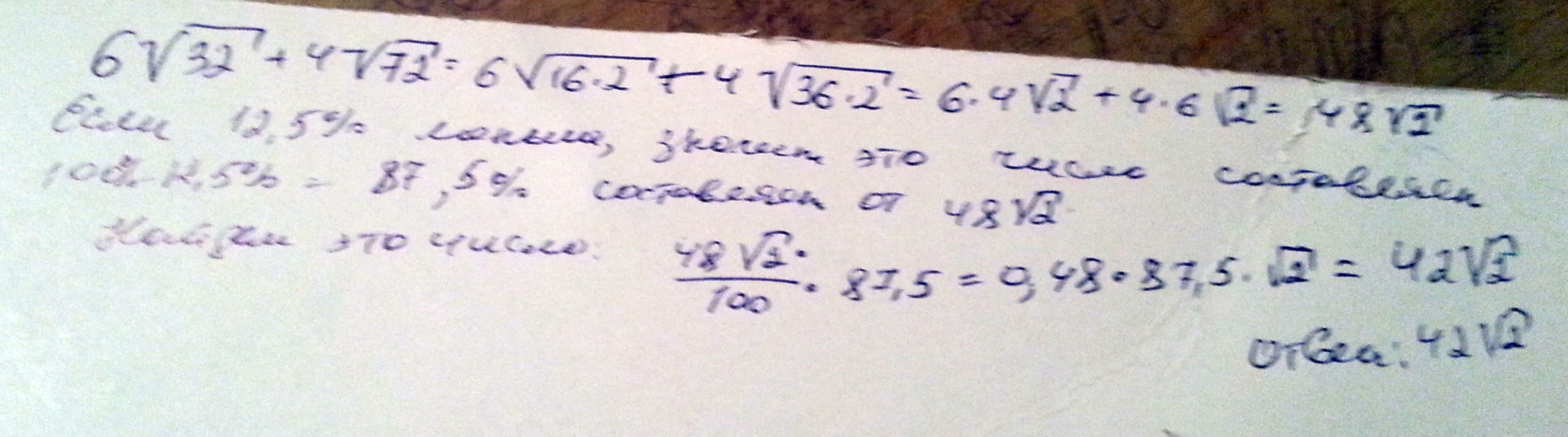
Напишите числа -5 и 2 выберите правильный ответ а)-5 больше чем 2 б) -5 меньше чем 2 в) -5 ровно 2
Найдите модуль числа-7
а) модуль -7=-7
б) модуль-7=7
в) модуль-7=0
Найдите суму чисел-15 и +8
а)-7
б)-23
в)7
г)23
Напишите числа противоположные числам 4.0.2.
Решите примеры
-27+40(-11)
Раскройте дужки, найдите значение примера
-37-(15-23)
Упростите пример
(14-а)-(-21-а)
Решение: -5 меньше чем 2модуль-7=7
-7
4=-4;0=0;-2=2
-467 если вы там знак никакой не забыли
-75
-5 меньше 2;
модуль -7 ровно 7;
-15+8=-7
число протилежне 4 це -4
0 це 0
-2 це 2
-27+40(-11)=40-27=13*-11 незнаю.



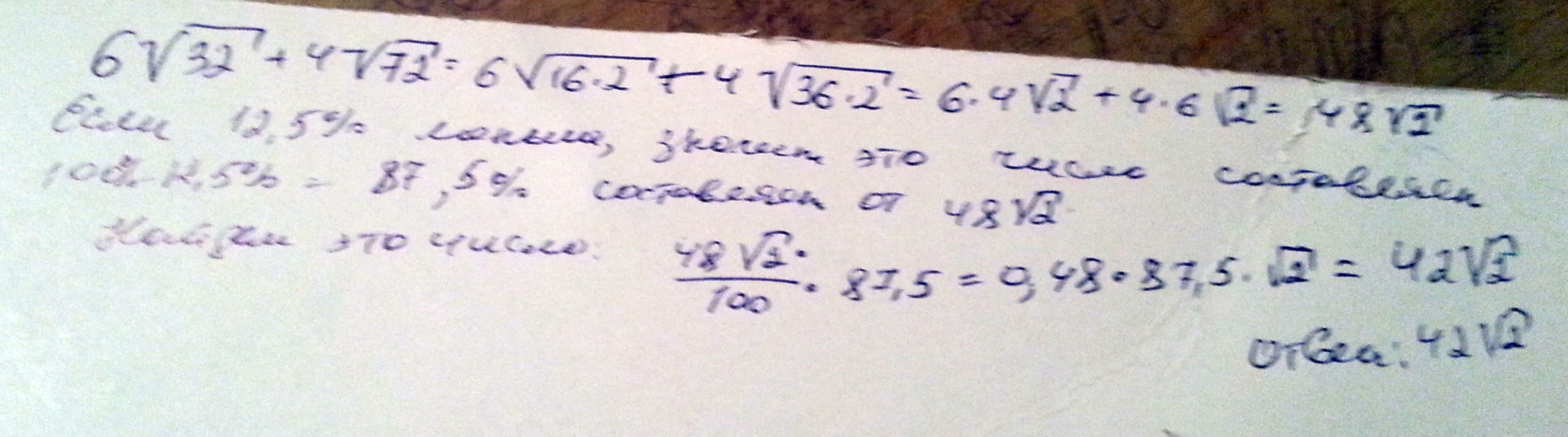
 Два противоположных числа, например +6 и -6, отличаются знаками, но записываются одинаковыми цифрами. Говорят, что они имеют одинаковые абсолютные величины. Абсолютная величина каждого из них равна 6.
Модулем (абсолютной величиной) положительного числа является само это число, модулем отрицательного числа - противоположное ему число, модулем числа 0 - само число 0. То есть под модулем числа понимается абсолютная величина, абсолютное значение этого...
Два противоположных числа, например +6 и -6, отличаются знаками, но записываются одинаковыми цифрами. Говорят, что они имеют одинаковые абсолютные величины. Абсолютная величина каждого из них равна 6.
Модулем (абсолютной величиной) положительного числа является само это число, модулем отрицательного числа - противоположное ему число, модулем числа 0 - само число 0. То есть под модулем числа понимается абсолютная величина, абсолютное значение этого... Уравнения с модулем
Пример 1. Решить уравнение |10х – 5| = 15.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15 │10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20 │10х = –15 + 5 = –10
↕
│х = 20 : 10 │х = –10 : 10
↕
│х = 2 │х =...
Уравнения с модулем
Пример 1. Решить уравнение |10х – 5| = 15.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15 │10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20 │10х = –15 + 5 = –10
↕
│х = 20 : 10 │х = –10 : 10
↕
│х = 2 │х =...