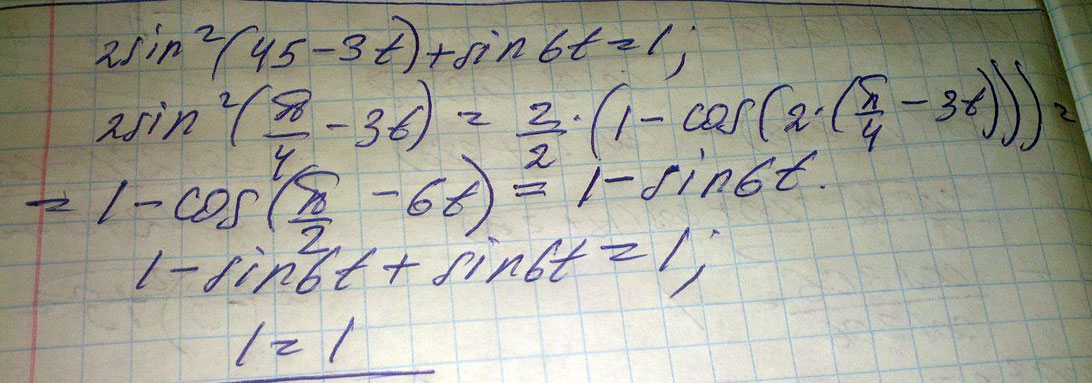тождество »
решите тождество - страница 2
Решить тождества
sin²a-cos²a= 1-2cos²a cos⁴a+sin²a cos²a+sin²a=1
Решение: $$ sin^2a-cos^2a=1-2cos^2a\\-(cos^2a-sin^2a)=sin^2a+cos^2a-2cos^2a\\-cos2a=-(cos^2a-sin^2a)\\-cos2a=-cos2a; $$
Вообще можно намного проще преобразовать правую часть, если знать формулу cos2a, а именно:
$$ cos2a=cos^2a-sin^2a=cos^2a-1+cos^2a=2cos^2a-1 \\ cos^4a+sin^2acos^2a+sin^2a=1\\cos^2a(sin^2a+cos^2a)+sin^2a=1\\cos^2a(1)+sin^2a=1\\cos^2a+sin^2a=1\\1=1 $$
Потребовалось лите основное тригонометрическое тождество:
$$ sin^2a+cos^2a=1 $$
Правильно ли тождество
(4cos4α * (1-sin8α)) / sin²4α = (8cos4α / sin²4α)* sin²(π/4 - 4α)
Решение: Домножим обе части на $$ \frac{sin ^{2}4 \alpha }{4cos4 \alpha } $$
Получим $$ 1-sin8 \alpha =2sin ^{2}( \frac{ \pi }{4} - 4 \alpha ) \\ 1-sin8 \alpha = (sin\frac{ \pi }{4}*cos4\alpha -cos \frac{ \pi }{4}*sin \alpha ) ^{2} \\ 1-sin8 \alpha = ( \frac{ \sqrt{2} }{2} )^{2} *(cos4 \alpha -sin4 \alpha )^{2} \\ 1-sin8 \alpha = \frac{1}{2}*(cos ^{2}4 \alpha -2cos4 \alpha sin4 \alpha +sin ^{2}4 \alpha ) \\ 1-sin8 \alpha = \frac{1}{2} *(1-sin8 \alpha ) \\ 1 eq \frac{1}{2} $$
Тождество неверно.Решите тождество)
2sin^2(45°-3t)+sin6t=1
Решение: Для начала переводите 45 градусов как pi/4. Далее - применяете формулу понижения степени у синуса, получаем: 1-cos(pi/2-6t). Видим - формулу приведения, преобразуем, получаем: 1-sin6t. Далее, обычная арифметика.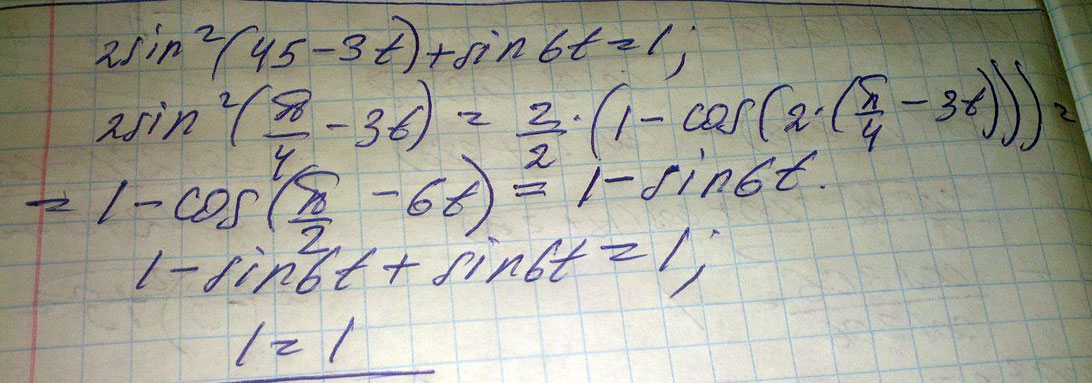
Lg(9+(lg(9+lg9))) < 1
sin 4x * tg2x = 4(sin^2x-sin^4x)
верны ли тождество
Решение: Lg(9+(lg(9+lg9))) < 1
lg9<1 9+lg9<10 lg(9+lg9)<1 9+ lg(9+lg9)<10.
Lg(9+(lg(9+lg9))) < 1 тождество верное
sin 4x * tg2x = 4(sin^2x-sin^4x)
остальное-во вложении
Укажите тождество ctg t * sin^2 t = (tg t + ctg t )^-1
Решение: Cost/sint*sint^2t=1/(sint/cost +cost/sint) в первом сокращаете синусы и получаете cost*sint а во втором приводите к общему знаменателю сумма квадрата синуса и кв косинуса будет равна 1 поэтому там останентся 1/1/ cost*sint которое равно cost*sint. для удобства можно обя части умножить и поделить на 2. 2/2*cost*sint=1/2*sin2t.
тождество доказано
1/2*sin2t= 1/2*sin2t.