тождество »
решите тождество - страница 3
Что такое тождество? приведите пример и решите его
Решение: То́ждество (в математике) — равенство, выполняющееся на всём множестве значений входящих в него переменных, например:
a^2 - b^2 = (a + b)(a - b)
(a + b)^2 = a^2 + 2ab + b^2
и т. п. Иногда называют тождеством также равенство, не содержащее никаких переменных; напр. 25^2 = 625.
Тождественное равенство, когда его хотят подчеркнуть особо, обозначается символом «То́ждество (в математике) — равенство, выполняющееся на всём множестве значений входящих в него переменных, например:
a^2 - b^2 = (a + b)(a - b)
(a + b)^2 = a^2 + 2ab + b^2
и т. п. Иногда называют тождеством также равенство, не содержащее никаких переменных; напр. 25^2 = 625.
Тождественное равенство, когда его хотят подчеркнуть особо, обозначается символом «\equiv».
Докажите тождество sinx-cosx=-√2cos(p/4+x) там минус корень из 2
Решение: 3 - 4cos2x + cos4x = 3 - 4cos2x + 2cos^2x - 1 = 2cos^2x - 4cos2x + 2 = = 2(cos2x - 1)^2 = 8sin^4x.
3 + 4cos2x + cos4x = 3 + 4cos2x + 2cos^2x - 1 = 2cos^2x + 4cos2x + 2 = 2(cos2x + 1)^2 = 8cos^4x.
Данная дробь равна 8sin^4x/8cos^4x = tg^4x.
2. 1 - 2sin^2x = cos2x = cos^x - sin^2x = (cosx - sinx)(cosx + sinx).
1 + sin2x = cos^x + sin^2x +2sinxcosx = (cosx + sinx)^2.
Вторая дробь после сокращений равняется (cosx - sinx)/(cosx+ sinx). Разделим числитель и знаменатель последней дроби на cosx и получим правую часть тождества.
3.
1 + sin2x = cos^x + sin^2x +2sinxcosx = (cosx + sinx)^2.
cos2x = cos^x - sin^x = (cosx - sinx)(cosx + sinx).
Данная дробь после сокращений равна (cosx + sinx)/(cosx - sinx). Умножим числитель и знаменатель на (корень из 2)/2 и получим правую часть тождества.пользуясь тождеством a^2 -b^2=(a-b)(a+b) разложите на множители:
а) x^2/3-4
б) а^4/3-5
в) м^1/2-25
г) 3-2х^1/3
д) с^0.8 - x^0.5
е) р-р^0.6
Решение: 1)(x^1/3-2)(x^1/3+2) 2)(a^2/3-корень из5)(a^2/3+корень из5) 3)(m^1/4-5)(m^1/4+5) 5)(c^2/5-x^1/4)(c^2/5+x^1/4) 6)(p^1/2-p^3/10)(p^1/2+p^3/10) 4 сделай по аналогии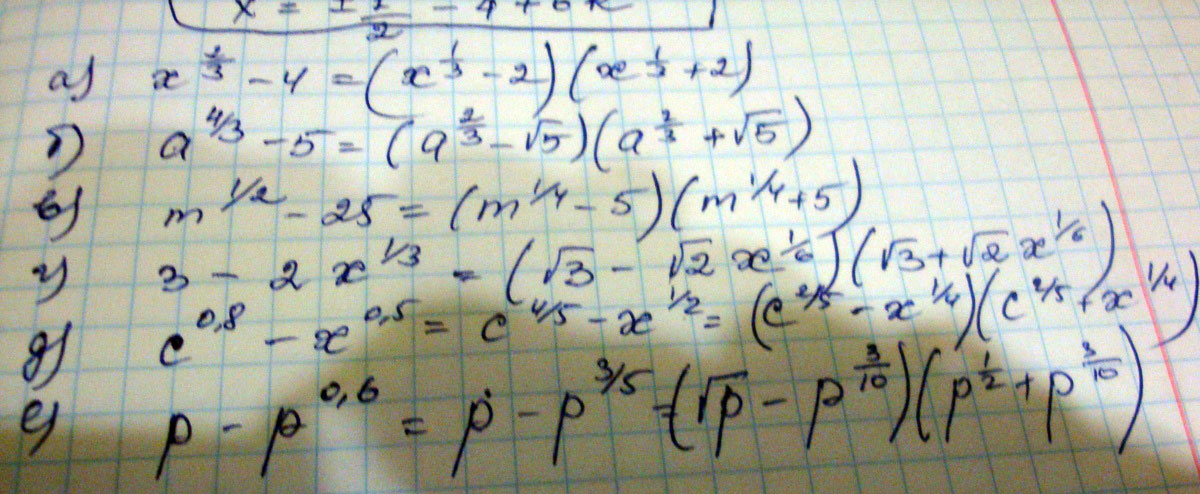
доведите тождество(доведіть тотожність) \( ( \frac{ \sqrt[4]{a}-5 }{ \sqrt[4]{a}+5} - \frac{ \sqrt[4]{a}+5 }{ \sqrt[4]{a}-5} ): \frac{10a^{ \frac{1}{4} }}{25-a^{ \frac{1}{2} }} =2 \)
Решение: $$ ( \frac{ \sqrt[4]{a}-5 }{ \sqrt[4]{a}+5} - \frac{ \sqrt[4]{a}+5 }{ \sqrt[4]{a}-5} ): \frac{10a^{ \frac{1}{4} }}{25-a^{ \frac{1}{2} }} = ( \frac{ a^{0.25}-5 }{ a^{0.25}+5} - \frac{ a^{0.25}+5 }{a^{0.25}-5} ): \frac{10a^{ 0.25 }}{25-a^{ 0.5} } = \\\ =\frac{ ( a^{0.25}-5)^2- ( a^{0.25}+5)^2 }{ (a^{0.25}+5)(a^{0.25}-5)} \cdot \frac{25-a^{ 0.5} }{10a^{ 0.25 }} = \\\ =\frac{ a^{0.5}-10a^{0.25}+25- a^{0.5}-10a^{0.25}-25 }{ a^{0.5}-25} \cdot \frac{25-a^{ 0.5} }{10a^{ 0.25 }} = \\ =-\frac{ -20a^{0.25} }{10a^{ 0.25 }} =2 $$
Докажите, что если в дроби (a^3-2b^3)\(3a^3-a^2b-4ab^2) переменные а и b заменить соответственно на pa и pb, то получим дробь, тождественно равную данной. Используя доказанное тождество, найдите значение заданной дроби при а=65, b=52
Решение: $$ \frac{a^3-2b^3}{3a^3-a^2b-4ab^2} \\\ \frac{(pa)^3-2(pb)^3}{3(pa)^3-(pa)^2pb-4pa(pb)^2} = \frac{p^3(a^3-2b^3)}{p^3(3a^3-a^2b-4ab^2)} = \frac{a^3-2b^3}{3a^3-a^2b-4ab^2} \\ a=65=5\cdot13 \\\ b=52=4\cdot13 $$
Значит, вместо чисел 65 и 52 можно подставить соответственно 5 и 4
$$ \frac{a^3-2b^3}{3a^3-a^2b-4ab^2}= \frac{5^3-2\cdot4^3}{3\cdot5^3-5^2\cdot4-4\cdot5\cdot4^2}=\\= \frac{125-128}{375-100-320}= \frac{-3}{-45}= \frac{1}{15} $$
Ответ: 1/15