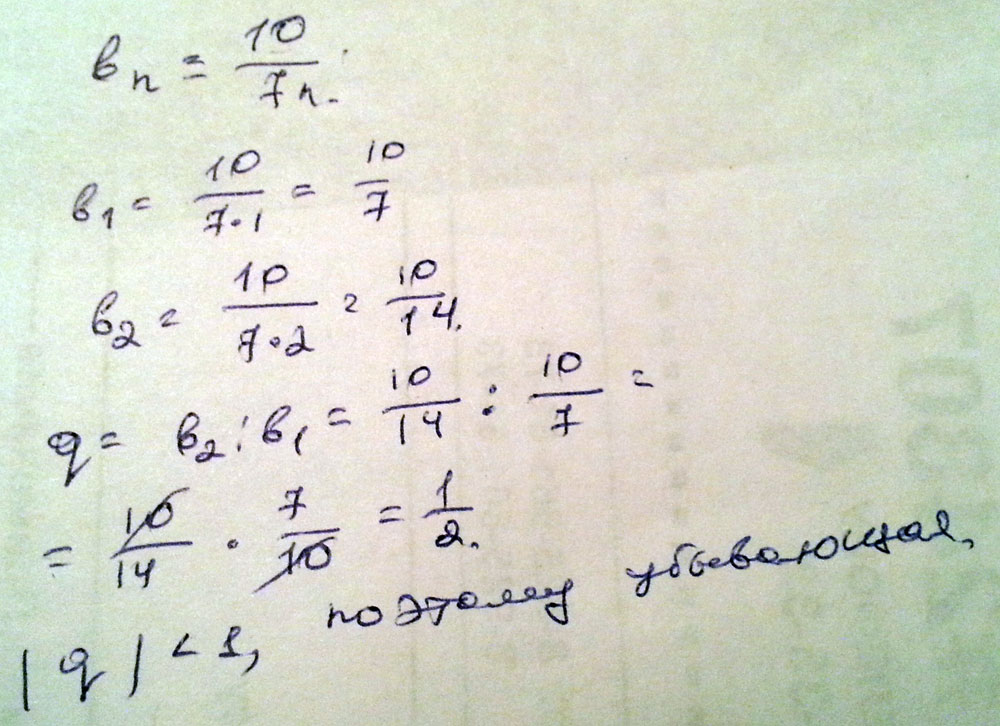прогрессия »

последовательность геометрической прогрессии

  • 1) Постройке график функции у= |1-(х+3)^2| и определите, при каких значениях c прямая у=c имеет с графиком ровно две общие точки.
    2) Из заданных последовательностей выберите геометрическую прогрессию. В ответ запишите знаменатель этой геометрической прогрессии.
    (аn): a1=5, an : an+1=2
    (bn): 4,6,8,10,
    (cn): 1, 1/2,1/3,1/4,


    Решение: 1. Нарисуем без модуля (рис), с добавлением модуля, все что ниже оси у зеркально отразиться. С рисунка видно, что у y=c с нашим графиком будет 2 точки пересечения про с=0 и при с>1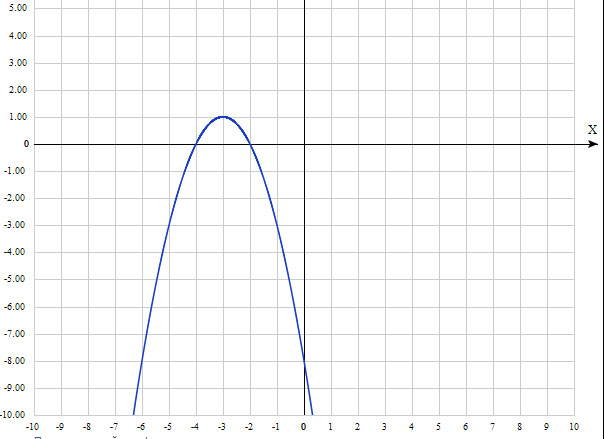

    . Нарисуем без модуля  рис с добавлением модуля все что ниже оси у зеркально отразиться. С рисунка видно что у y c с нашим графиком будет точки пересечения про с и при с...

  • Последовательность (Хn)-геометрической прогрессии(Cn), если : а) С5=-6, С7=-54 б) С6=25, С8=4


    Решение: $$ \\a)\quad C_5=-6;\quad C_7=-54\\C_5=C_1\cdot q^4\Rightarrow C_1=\frac{C_5}{q^4}\\C_7=C_1\cdot q^6\Rightarrow C_1=\frac{C_7}{q^6}\\\frac{C_5}{q^4}=\frac{C_7}{q^6}\Rightarrow C_5\cdot q^6=C_7\cdot q^4\Rightarrow q^2=\frac{C_7}{C_5}=\frac{-54}{-6}=9\\q=\pm3 $$

    $$ \\b)\quad C_6=4;\quad C_8=26\\C_6=C_1\cdot q^5\Rightarrow C_1=\frac{C_6}{q^5}\\C_8=C_1\cdot q^7\Rightarrow C_1=\frac{C_8}{q^7}\\\frac{C_6}{q^5}=\frac{C_8}{q^7}\Rightarrow q^2=\frac{C_8}{C_6}=\frac{25}4\\q=\pm\frac52=\pm2,5 $$

  • Какую последовательность называют геометрической прогрессией? что называют знаменателем геометрической прогрессии?


    Решение: Геометрическая прогрессия - бесконечный ряд чисел, в котором каждое последующие число равно придыдущему умноженному на определённый постоянный множитель

    Знаменатель геометричесской прогресси это определённое числочисло на которое умножается каждое последующее число

    Геометрическая прогрессия - последовательность, каждый член который отличается от предыдущего в q раз. Формула геометрической прогрессии $$ a_{n}=a_{1}*q^{n-1} $$

    А q- знаменатель геометрической прогрессии.

  • Является ли последовательность убывающей геометрической прогрессией если bn=10/7n


    Решение: B1=10/7; b2=10/14; b3=10/21. Видим, что числитель постоянный, а знаменатель возрастает, то есть значение дроби уменьшается. То есть последовательность убывающая.

    B b b . Видим что числитель постоянный а знаменатель возрастает то есть значение дроби уменьшается. То есть последовательность убывающая....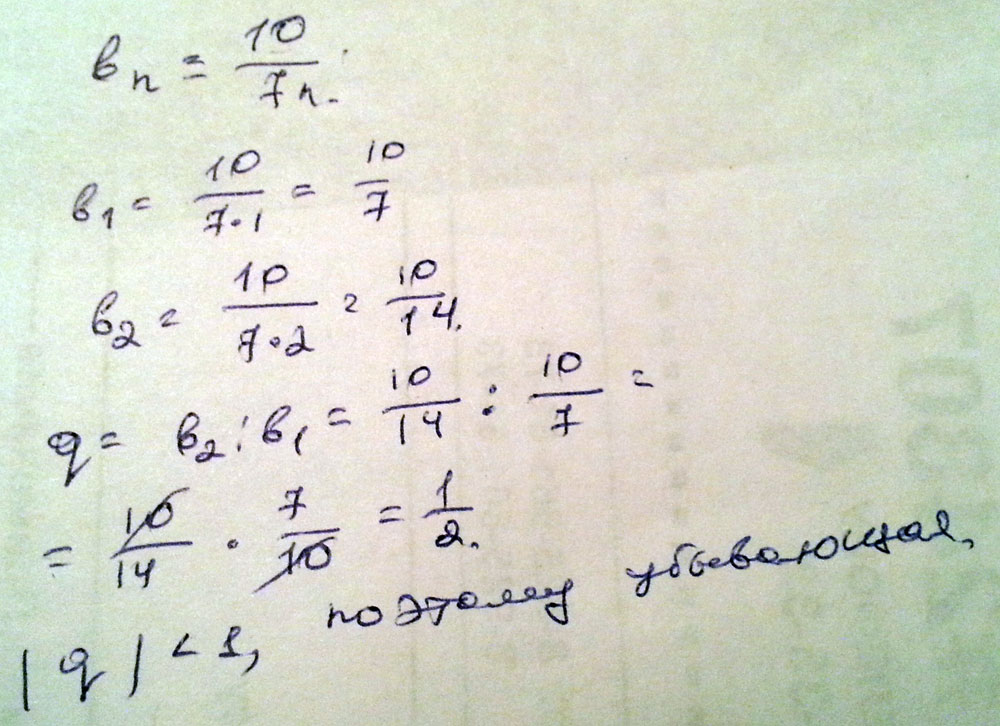

  • 1) Какая последовательность является геометрической прогрессией? а) 1;4;9;16. б)30; 0,3; 0,03; 0,003 в)40; 5; 5/8; 5/64


    Решение: Исходя из свойств геометрической прогрессии: b2 = V(b1*b3), V - знак корня. Данному условию соответствует только пункт в: пусть b1=40, тогда b3=5/8. Подставим в формулу: V(40*5/8) = V25 = 5 верно, т. к. b2=5 => это геометрическая прогрессия, у которой знаменатель равен 1/8. 4 число также соответствует геометрической прогрессии т. к. 5/8 * 1/8 = 5/64=b4

1 2 > >>