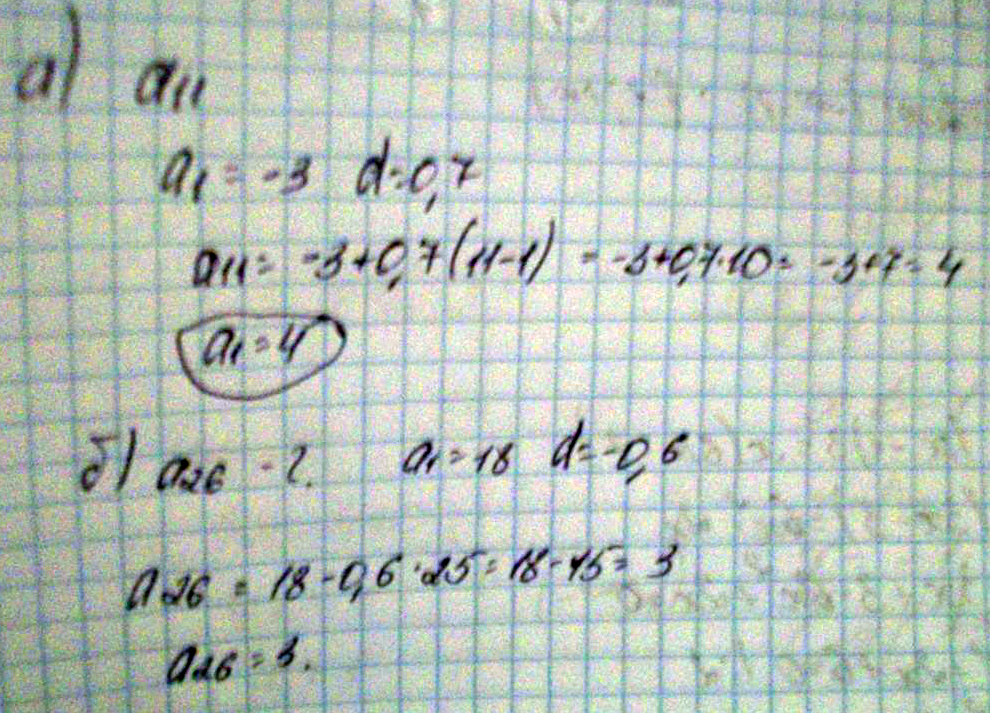последовательность образует арифметическую прогрессию
Какая из последовательностей, заданных формулой n-го члена является арифметической прогрессией?
1) a_n=2_n^2+1; 2) a_n=-1,2(дробь)n+1;
3) a_n=1 дробь 5-n ; 4) a_n=3*5^n.
Решение: Арифметическая прогрессия обладает следующим свойством: каждый член ар. прог. начиная со второго равенсреднему арифметическому предыдущего и последующего членов.
1) аn=2n²+1
a₁=3 a₂=9 a₃=19⇒(19+3)/2≠9⇒не прогрессия
2)an=-1/2n+1=-0,5n+1
a₁=0,5 a₂=0 a₃=-0,5⇒(0,5-0,5)/2=0⇒прогрессия
3)an=1/5-n
a₁=-4/5=-0,8 a₂=-1 4/5=-1,8 a₃=-2 4/5-2,8⇒(-0,8-2,8)/2=-1,8⇒прогрессия
4)an=3*5^n
a₁=15 a₂=75 a₃=375⇒(375+15)/2=75⇒не прогрессия
Для каждой последовательности из левого столбца поставьте в соответствие верное утверждение из правого столбца.
а) 0; 1/5; 2/5; 3/5;.
б) -50; -70; -90;.
в) 34; 33; 31; 28;.
1) Последовательность не является арифметической прогрессией.
2) Последовательность-возрастающая арифметическая прогрессия
3) последовательность - убывающая арифметическая прогрессия.
Решение: а) 0; 1/5; 2/5; 3/5;. 2) Последовательность-возрастающая арифметическая прогрессияб) -50; -70; -90;.3) последовательность - убывающая арифметическая прогрессия.
в) 34; 33; 31; 28;.1) Последовательность не является арифметической прогрессией.
если что-то будет не понятно обращайся
а - 2 ( возраст)
б - 1 (не явл)
в - 3 (убывающ)
для некоторой последовательности a1 a2 a3.an. верно равенство: 1/ (a1*a2) + 1/(a2*a3) + 1/(a3*a4) +.+ 1/(ak-1*ak) = (k-1) / (a1*ak). Докажите что эта последовательность - арифметическая прогрессия
Решение: $$ \frac{1}{a_1a_2}+.+\frac{1}{a_{k-1}a_k} = \frac{k-1}{a_1a_k}\\ \frac{1}{a_1a_2}+.+\frac{1}{a_{k}a_{k+1}} = \frac{k}{a_1a_{k+1}}\\ $$вычтем из второго первое
$$ \frac{1}{a_{k}a_{k+1}} = \frac{k}{a_1a_{k+1}}- \frac{k-1}{a_1a_k}\\ \frac{a_1}{a_1a_{k}a_{k+1}} = \frac{ka_k}{a_1a_ka_{k+1}}- \frac{(k-1)a_{k+1}}{a_1a_ka_{k+1}}\\ a_{k+1} = \frac{ka_k - a_1}{k-1} = a_k + \frac{a_k-a_1}{k-1} $$
Обозначим $$ d = a_2-a_1 $$
тогда для $$ a_2 = a_1 + d $$
предположим, что выполняется $$ a_k = a_1 + (k-1)d $$ для некоторого k, тогда
$$ a_{k+1} = a_k + \frac{a_k-a_1}{k-1} = a_1 + (k-1)d + \frac{a_1+(k-1)d - a_1}{k-1}=\\ =a_1 + (k-1)d + d = a_1 + kd $$
Следовательно последовательность является арифметической.
последовательность(an)-арифметическая прогрессия. найдите а) а11, если а1=-3 и d=0,7; б) а26, если а1=18 и d=-0,6
Решение: а1=4 Б) а26=3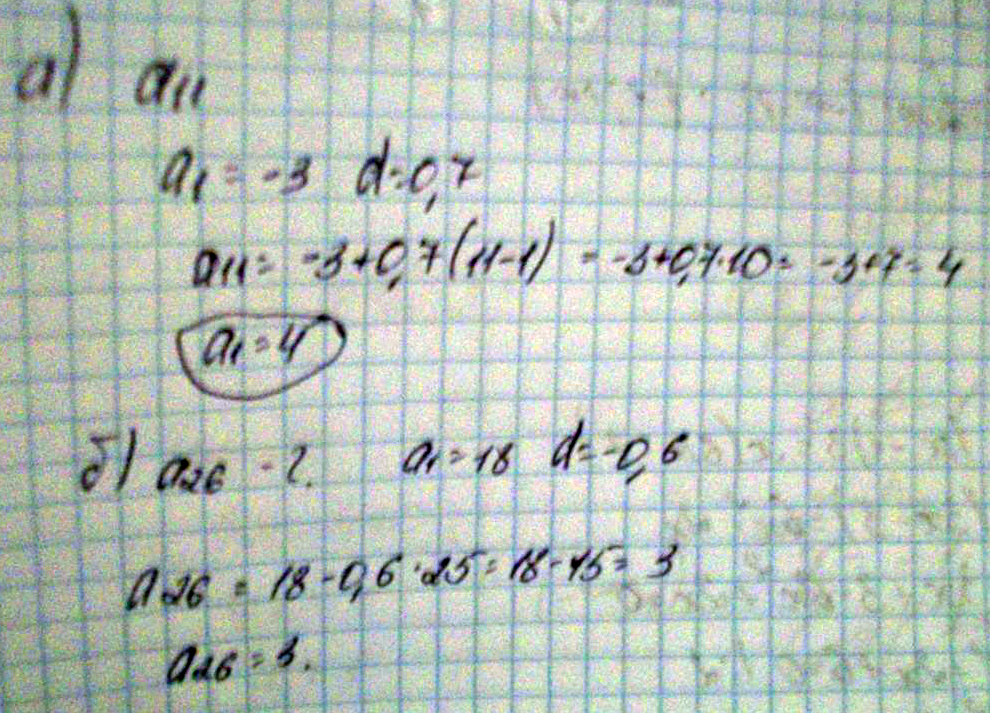
Арифметическая прогрессия начинается так: 16;12;8;. Какое число стоит в этой последовательности на 71-м месте?
Решение: Между членами прогрессии есть разность. Обозначим три данных числа так, что бы было понятно.
a1=16, a2=12, a3=8
Разность находиться по формуле d=a(n)-a(n-1)
То есть в нашем случае d=a2-a1, d=12-16=-4
То есть если разность d равна -4, то каждый член уменьшается на 4 единицы.
Формула нахождения n-ого члена такая a(n)=a1+d(n-1)
То есть в нашем случае нужно найти 71 член прогрессии. Тогда подставляем в формулу a71=16+(-4)*70
a71=16-280=-264
Ответ: -264