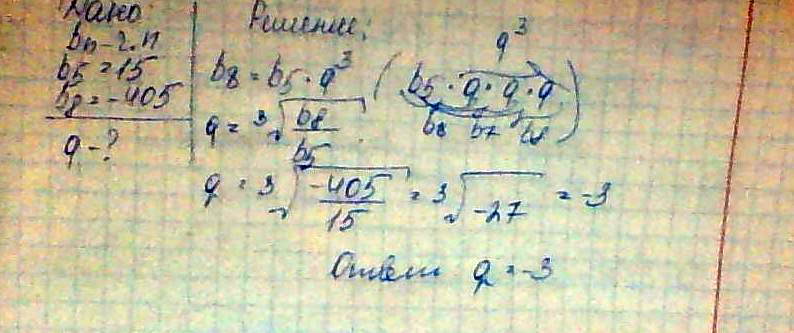прогрессия »

знаменатель прогрессии

  • В геометрической прогрессии bn, известны b5=1, b7=1/4. Найдите положительный знаменатель прогрессии


    Решение: b5=1, b7=1/4. Найдите   положительный  знаменатель   прогрессии
    b7/b5=b1q^6/b1q^4=q^2=1/4/1=1/4
    bn=b1q^(n-1)
    q²=1/4
    q=1/2

  • В геометрической прогрессии (an): а3=2, а6=1//4 (Одна четвертая).

    Найдите знаменатель прогрессии (аn)


    Решение: а3=а1*q во 2-й степени

    а6=а1*q в пятой степени

    Система уравнений:

    2=а1*q в квадрате

    1/4=а1* q в пятой 

    а1=2 разделить на q в квадрате

    подставляем в нижнее уравнение системы:

    1/4=2*q в пятой/q в квадрате

    1/4=2*q в кубе

    q в кубе=1/(2*4)

    q в кубе= 1/8

    q= корень кубический из 1/8

    q=1/2

  • Дана геометрическая прогрессия bn для которой b3=12, b6= -96 НАЙДИТЕ ЗНАМЕНАТЕЛЬ ПРОГРЕССИИ


    Решение: Решение:
    Воспользуемся формулой:
    b_n=b1*q^(n-1)  Отсюда:
    b3=b1*q^(3-1)  или  12=b1*q^2
    b6=b1*q^(6-1) или -96=b1*q^5
      Разделим второе выражение на первое, получим:
    b1q^5/b1q^2=-96/12
    q^3=-8
    Извлечём кубический корень из (-8), получим q=-2
    Ответ: знаменатель геометрической прогрессии равен: -2

  • Дана геометрическая прогрессия bn для которой b5=15;b8=-405 найдите знаменатель прогрессии


    Решение: По определению геометрической прогрессии имеем право выкарабкаться без мучительных систем(можно и так, но там q придётся угадывать),
    вот смотрите, что можно сделать:

    Выразим В5 и В8 через В1
    В5 = В1 * q^4
    B8 = B1 * q^7
    разделим В8 на В5
    В1 * q^7 / B1 * q^4 = - 405 / 15.B1 сокращаются, остаётся. q^7 / q^4 = q^3. q^3 = - 27. откуда q = -3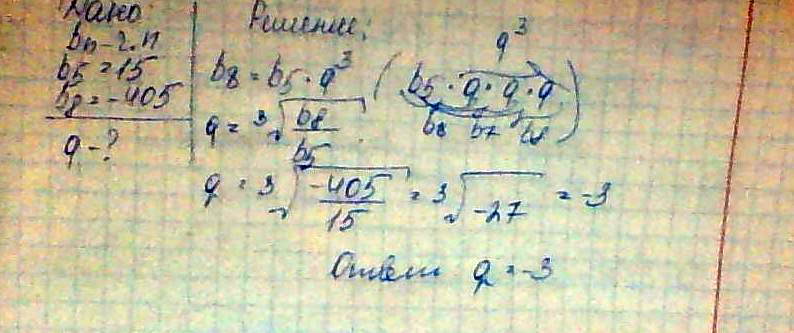

    По определению геометрической прогрессии имеем право выкарабкаться без мучительных систем можно и так но там q прид тся угадывать вот смотрите что можно сделать Выразим В и В...

  • Дана геометрическая прогрессия (bn), в которой b3=12,b6=-96. Найдите знаменатель прогрессии.


    Решение: Решение:
    Воспользуемся формулой:
    b_n=b1*q^(n-1)  Отсюда:
    b3=b1*q^(3-1)  или  12=b1*q^2
    b6=b1*q^(6-1) или -96=b1*q^5
      Разделим второе выражение на первое, получим:
    b1q^5/b1q^2=-96/12
    q^3=-8
    Извлечём кубический корень из (-8), получим q=-2
    Ответ: знаменатель геометрической прогрессии равен: -2

    $$ b_3=12;\\ b_6=-96;\\ b_n=b_1\cdot q^{n-1};\\ b_3=b_1\cdot q^2;\\ b_6=b_1\cdot q^5;\\ \frac{-96}{12}=\frac{b_6}{b_3}=\frac{b_1\cdot q^5}{b_1\cdot q^2}=q^3=-8;\\ q=\sqrt[3]{-8}=-2 $$

1 2 > >>