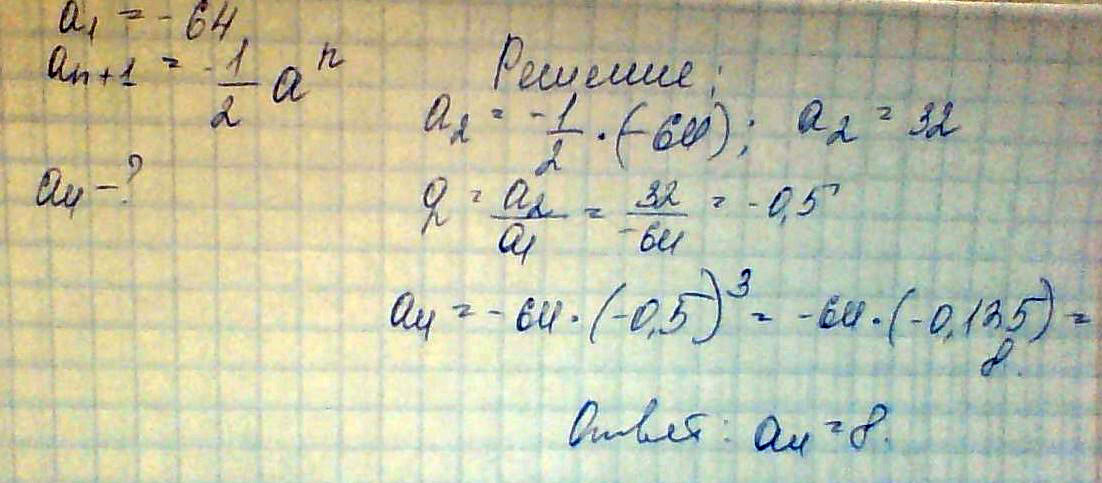геометрическая прогрессия задана условиями
геометрическая прогрессия задана условиями b(1)=7, b(n+1)=2b(n)
в скобки взято то, что пишется ниже b.
Решение: b[n+1]=2b[n]b[2]=2*b[1]=2*7=14
b[3]=2*b[2]=2*14=28
b[4]=2*b[3]=2*28=56
сумма первых 4 членов данной геометрической прогрессии равна
S[4]=b[1]+b[2]+b[3]+b[4]
S[4]=7+14+28+56=105
ответ: 105
или иначе
по формуле общего члена геомтрической прогрессии
b[n+1]=b[n]*q^n
b[2]=b[1]*q
b[n+1]=2*b[n]
b[2]=2*b[1]
поєтому q=2
по формуле суммы первых членов геометрической прогрессии
S[n]=b[1]*(q^n-1)/(q-1)
S[4]=7*(2^4-1)/(2-1)=105
ответ: 105
Геометрическая прогрессия задана условиями: b1=3, bn+1=3bn. Укажите число, являющееся данной геометрической прогрессии.
1) 6; 2) 12; 3) 24; 4) 27.
Решение: Формула n-го члена геометрической прогрессии имеет вид: bn=b1*q^(n-1), кроме того суть геометрической прогрессии - n+1 -й член прогрессии получается умножением bn на q. То есть первый член умножить на q будет второй член его умножить на q - будет третий и так далее. Коротко говоря, отношение bn+1/bn =q=const. В нашем примере
bn+1/bn=3, ⇒q=3 b1=3 bn =3q^(n-1)=3*3^(n-1)
воспользуюсь подсказкой модератора - мое решение более сложное.
Выпишем члены прогрессии - при n=1 это 3 ( 3*3^0), n=2
n=2 3*3^1 будет 9, и далее 27, 81.
выпишем еще раз члены прогрессии 3, 9, 27, 81 у нас есть только 27
Ответ: 27
Примечание. Такое решение проще, но оно несколько неудобно при иной постановке задачи. Скажем, нужно узнать число 2016 это член прогрессии или нет? нам трудно выписать столько членов прогрессии. Мы можем сразу выяснить - делится число на 3? Если нет, то 3*3^(n-1) не имеет решения в натуральных числах. 3*3^(n-1)=m ⇒
m делится на 3. Число 2016 делится на 3 так как сумма его цифр 2+1+6=9 делится на три. Если записать p=m/3, то 3^(n-1) = p. У нас, например, 2016/3=р=672 и теперь надо узнать это степень числа 3 или нет? Здесь без выписывания степеней тройки в табличку.
Повторим предыдущее, если 672 не делится на 3, то ответ - не принадлежит 672 прогрессии. Однако, 6+7+2=15 и деление на 3 есть. 672/3=224 - здесь 2+2+4=8 и нет деления 224 на 3. И, значит исходное число 2016 не член прогрессии. Заметим, по существу мы проводим разложение 2016 на простые множители.
Еще можно рассуждать так: Выпишем степень 3 так, чтобы 3^(k-1)≤672≤3^k и если равенства нет, то исходное число не член прогрессии. 3^5=243 3^6=729 и ясно - 2016 не член прогрессии.Геометрическая прогрессия задана условием \( a_1=-64; a_{n+1}= -\frac{1}{2}^{a^{n}} \) Найдите \( a_{4} \)
Решение: ВАМ ПРОГРЕССИЮ ЗАДАЛИ РЕКУРРЕНТНО, ЭТО ЗНАЧИТ, ЧТО ДАЛИ ФОРМУЛУ СЛЕДУЮЩЕГО ЧЛЕНА.
А что делать с рекуррентной формулой? Подставлять первый член, искать второй, находить знаменатель, и только потом по формуле n-ого члена ищем 4.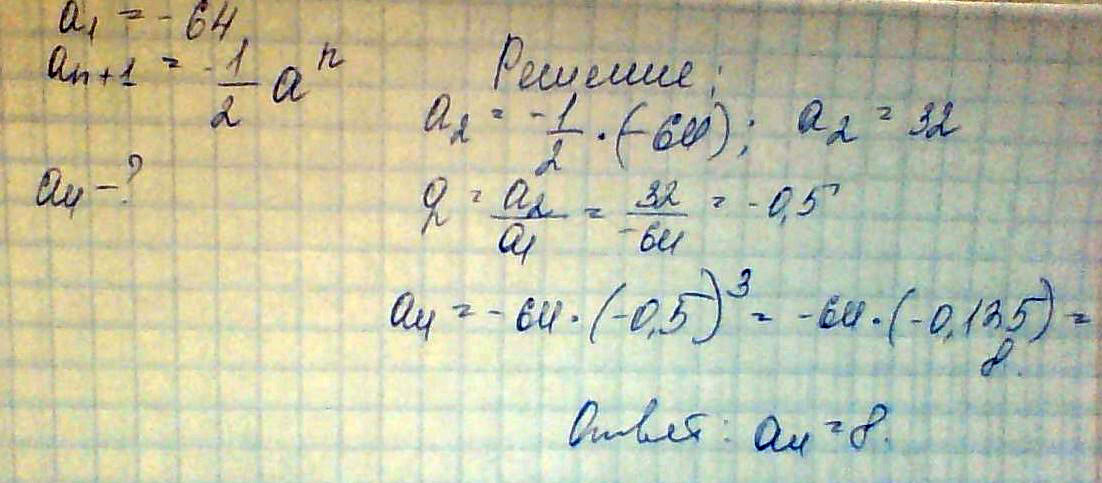
Геометрическая прогрессия (аn) задана условиями : а3 = -3, а8 = -96. Найдите знаменатель этой прогрессии
Решение: Знаменатель геом. прогрессии qq^5=a8/a3=-96/-3=32
q=2
По формуле n-го члена геометрической прогрессии an=a₁* q^(n-1)
а₃ = а₁ * q² = -3
а₈ = а₁ * q⁷ = -96 => а₁ = -96/q⁷ (подставим в первое ур-ние)
-96/q⁷ * q² = -3
-96/q⁵ = -3
q⁵ = -96 / -3
q⁵ = 32
⁵√q⁵ = ⁵√32
q = 2
Ответ: q = 2.
Геометрическая прогрессия (bn ) задана условиями: b1 = 4, bn + 1 = 2bn.
Найдите b7.
Решение: в1=4 и просто в1 подставляй в формулув2=8
в3=16(потом просто на 2 умножай)
в4=32
в5=64
в6=128
в7=256
Ответ:256
b=4;
b(n+1)=2bn - означает, что q(знаменатель)=2
b7=b1*q^(7-1)=b1*q^6=4*2^6=256
Ответ: b7=256
