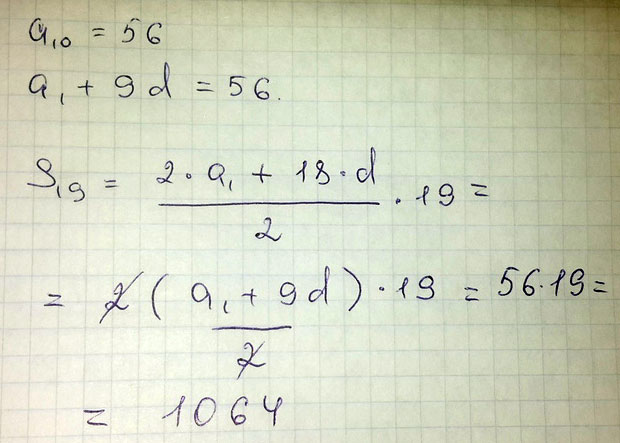прогрессия »
найдите n член прогрессии - страница 24
Найдите первый отрицательный член арифметической прогрессии: 113, 106, 99,
Решение: d=-7 следовательно a1=-6$$ a_1=113; a_2=106;\\ d=a_2-a_1=106-113=-7;\\ a_n=a_1+(n-1)*d;\\ a_n=113+(n-1)*(-7)=113-7n+7=120-7n;\\ a_n<0;\\ 120-7n<0;\\ 120<7n;\\ \frac{120}{7} $$
наименьшее число (номер первого отрицательного члена аифмитической прогрессии из последнего неравенства равен 18)
$$ a_{18}=113+(18-1)*(-7)=-6 $$
ответ: -6
В арифметической прогрессии известно, что а10=56. Найдите сумму 19-ти членов этой прогрессии.
Решение: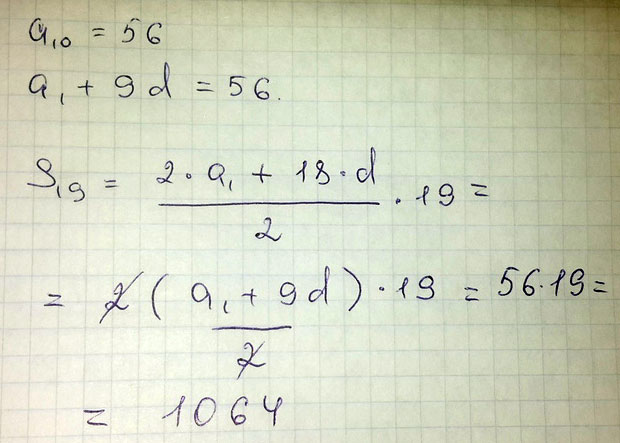
Последовательность а(n) -арифметическая прогрессия. Найдите сумму шести её членов, если а2=11, а3=8, а4=5
Решение: a3=a1+2d a2=a1+d8=a1+2d 11=a1+d
решаем систему
8=a1+2d
11=a1+d
a1=8-2d
11=8-2d+d
a1=8-2d
11=8-d
a1=8-2d
8-d-11=0
a1= 8-2d
-d-3=0
a1=8-2d
-d=3
a1=14
d=-3
a6=a1+5d => a6=14-15=-1
S=(a1+an)*n/2 => S= (14-1)*6/2= 13*3=339
Ответ:39
Найдите арифметическую прогрессию, в которой среднее арифметическое n первых ее членов равно 2n
Решение: По определению среднее арифметическое равно общей сумме членов деленное на их общее количество:
$$ \frac{a_1+a_2+.+a_n}{n}=\frac{S_n}{n}=2n $$
откуда сумма n первых членов арифметической последовательности равна
$$ S_n=2n^2 $$
в частности
$$ S_1=a_1=2*1^2=2 \\ S_2=a_1+a_2=2*2^2=8 $$
отсюда второй член последовательности равен
$$ a_2=S_2-S_1=8-2=6 $$
разность арифметической прогрессии равна
$$ d=a_2-a_1=6-2=4 $$
значит искомая арифметическая прогрессия это арифметическая прогрессия с первым членов 2, и разностью арифметической прогрессии 4
(2, 6, 10, 14, 18,)
-
///////////
маленькая проверочка схождения с формулой суммы членов прогрессии
$$ a_1=2;d=4 \\ S_n=\frac{2a_1+(n-1)*d}{2}*n \\ S_n=\frac{2*2+(n-1)*4}{2}*n=(2+2(n-1))n=(2+2n-2)n=2n^2 $$
//////////
ответ: арифметичесская прогрессия с первым членом 2 и разностью прогрессии 4