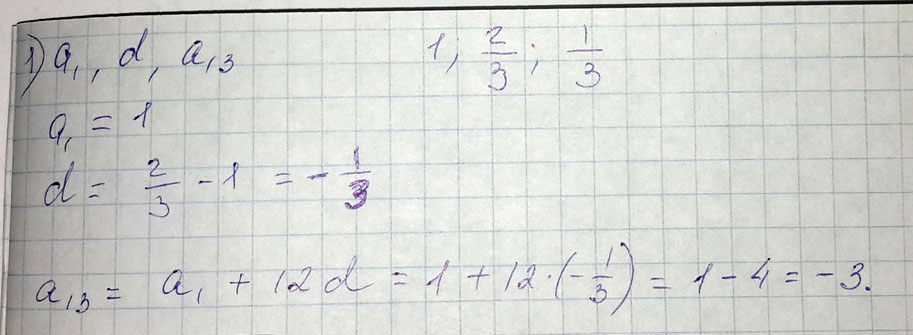прогрессия »
найдите n член прогрессии - страница 22
1) найдите первый отрицательный член арифметической прогрессии an в которой a1=10 d=-0,2. Проверьте свой ответ.
2) в арифметической прогрессии yn известны пятый и шестой члены : y5=-150
y6=-147. Сколько членов этой прогрессии отрицательны?
Решение: 1) дано:
а1=10, d=-0.2
по формуле an=a1+(n-1)d
подставляем числа:
а10=10+(10-1)(-0.2)=10-1.8=8.2(до отрицательного нам еще далеко, поэтому берем число больше)
а51=10+(51-1)(-0.2)=10-10=0(число по-прежнему не отрицательное)
а52=10+(52-1)(-0.2)=10-10.2=-0.2(самое первое отрицательное число)
Ответ: а521) найдите a1,d,a13 для арифметической прогрессии(an):1;2\3;1\3
2) Являются ли числа A=99 и B=-10 членами арифметической прогрессии(аn), если an=0,5n-1
3) В арифметической прогрессии 1\4; 1\6. укажите номер того члена, начиная с которого все члены прогрессии будут меньше -1
Решение: 1) найдите a1,d,a13 для арифметической прогрессии(an):1;2\3;1\3
a1=1
d=-1/3
a12=a1+11*d=1-11/3=-8/3
2) Являются ли числа A=99 и B=-10 членами арифметической прогрессии(аn), если an=0,5n-1
99=0.5n-1
100=0.5n
n=200 да
-10=0.5-1
0.5n=-9 нет N должно быть больше 0
3) В арифметической прогрессии 1\4; 1\6. укажите номер того члена, начиная с которого все члены прогрессии будут меньше -1
D=1/6-1/4=-1/12
an=a1+(n-1)d<0
1/4-1/12(n-1)<0
1/4+1/12<1/12n
n>4"""""""""""""""""""""""""""""""""
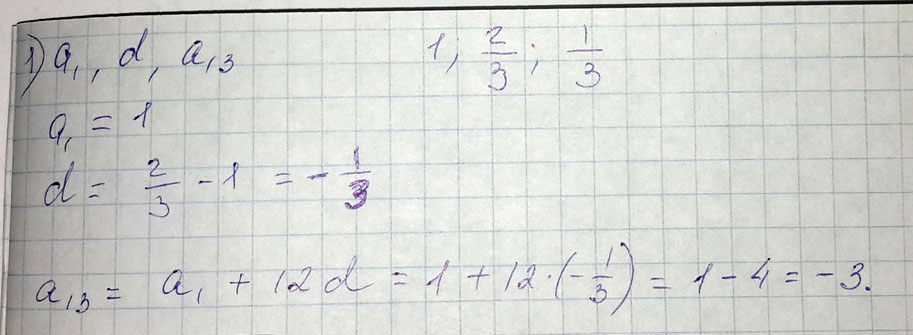
Найдите номер члена арифметической прогрессии равного 22, если а3,=-2, d=3
Решение: Сначала найдем $$ a_{1} $$:
$$ a_{n}= a_{1}+d(n-1) $$
$$ a_{3}=a_{1}+d(3-1) $$
$$ -2= a_{1}+2d $$
$$ -2= a_{1}+2d $$
$$ a_{1}=-2-6 $$
$$ a_{1}=-8 $$
Теперь при помощи той же формулы мы можем найти номер члена ариф. прогрессии:
$$ a_{n}= a_{1}+d(n-1) $$
$$ 22=-8+3(n-1) $$
$$ 22=-8+3n-3 $$
$$ 3n=22+8+3 $$
$$ 3n=33 $$
$$ n=11 $$
Найдите первый член арифметической прогрессии, если а6=23, а11=48
Решение: По формуле n-ого члена арифметической прогрессии мы можем записать следующие уравнения относительно а6 и а11:
23=а1+5d,
48=a1+10d.
Из второго уравнения вычитаем первое и находим а1:
25=5d, отсюда d=5.
Подставляем это значение d в первое уравнение и находим а1:
23=а1+5*5, а1=-2.Известны два члена арифметической прогрессии a5=8,2 и a10=4,7. Найдите первый член арифметической прогрессии
Решение: Арифметической прогрессией называется такая последовательность чисел, в которой разность между последующим и предыдущим членами остается неизменной. Эта неизменная разность называется разностью прогрессии.
Тогда эта разность равна (а10-а5)/5=(4,7-8,2)/5= -3,5/5=-0,7
Отсюда а1=а5-(-0,7)*5= 8,2-(-3,5)=8,2+3,5=11,7
Ответ: а1=11,7.