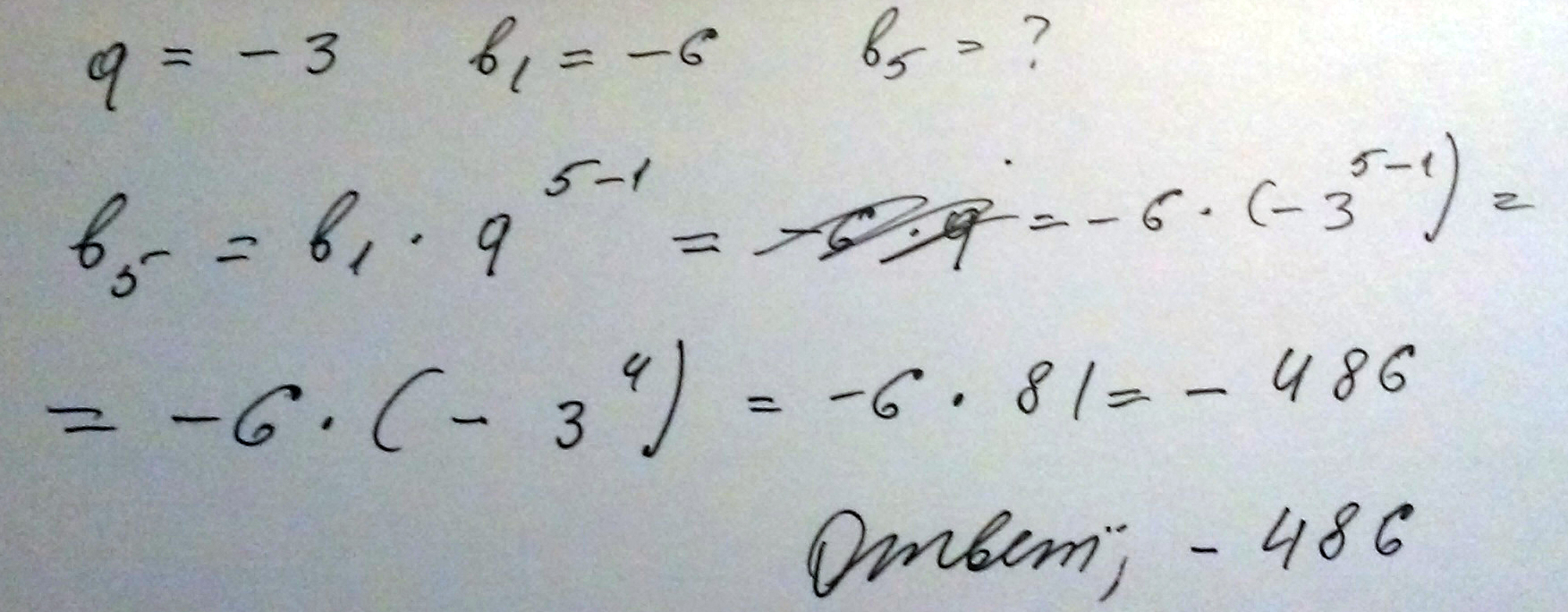прогрессия »

дана геометрическая прогрессия - страница 2

  • дана геометрическая прогрессия у которой b1=2, q=3, bn=54 Найти n


    Решение: b1=2

    q=3

    bn=54

    bn=b1*q^(n-1)

    2*3^(n-1)=54

    3^(n-1)=27

    3^(n-1)=3^3

    n-1=3

    n=4

    Ответ 4

    в1=2

    g=3

    вп=54

    по формуле 

    вп=в1*g"(п-1)

    54=2 * 3"(п-1)

    3"(п-1)=27

    3"(п-1)=3"3

    п-1=3

    п=4

    Ответ: п=4

  • Дана геометрическая прогрессия (bn), знаменатель которой равен -3, b1= -6. Найдите b5.


    Решение: $$ q=-3 $$
    $$ b_1=-6 $$
    $$ b_n=b_1* q^{n-1} $$
    $$ b_5=b_1* q^{4} $$
    $$ b_5=-6*(-3)^4=-6*81=-486 $$

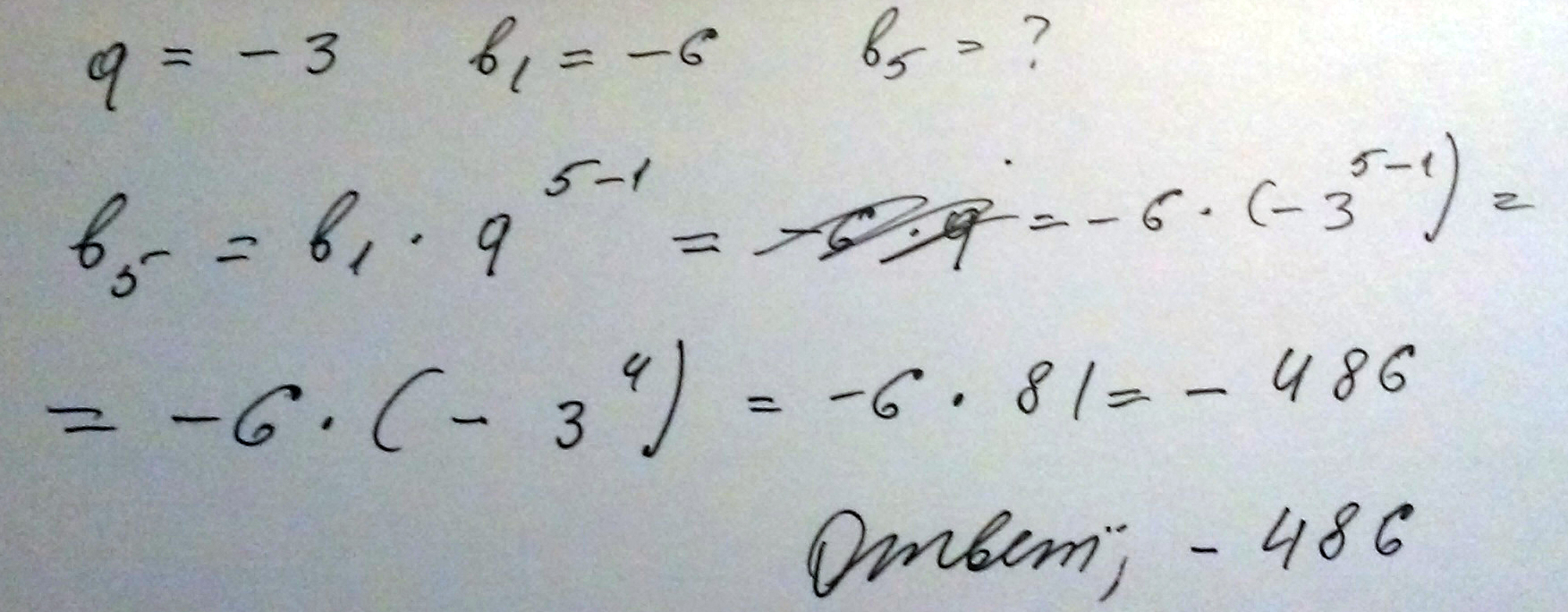
    q - b - b n b q n- b b q b - - - -...

  • Дана геометрическая прогрессия (bn). Найдите b1,q,S8, если bn =4/2 в степени 3-n
    9класс


    Решение: первый член прогрессии будет равен 1, второй член 2, тогда разность будет равна 

    2 делить на 1= 2

    сумма восьми членов по формуле S=255

    первый член прогрессии будет равен второй член тогда разность будет равна  делить на сумма восьми членов по формуле S...

  • Дана геометрическая прогрессия (bn). Найдите b1, если q=(√3)/3 b6=-1/√3.


    Решение: Нам известна формула для нахождения n-ого члена геометрической прогрессии:

    $$ b_n=b1*q^(n-1) $$

    Где bn=b6=-1/√3.

    -1/√3=-√3/3. (-1/√3)*(√3/√3)=-√3/3. (Избавляемся от корня в знаменателе).

    q - знаменатель.

    А n в степени - это порядковый номер члена прогрессии, в нашем случае это 6.

    Выражаем b1: $$ b1=\frac{b_n}{q^(n-1)};\\ $$

    Считаем:

    $$ b1=\frac{-1}{\sqrt{3}}:(\frac{\sqrt{3}}{3})^5;\\ b1=\frac{-\sqrt{3}}{3}*(\frac{3}{\sqrt{3}})^5;\\ b1=\frac{-\sqrt{3}}{3}*\frac{243}{9\sqrt{3}};\\ b1=\frac{-243}{27};\\ b1=-9;\\ $$

    Главное не допустить ошибку в счете. Сначала возводим в 5-ую степень, а далее сокращаем.

    Получаем ответ: b1=-9.

  • Дана геометрическая прогрессия
    b5(5)-b3(3)=1200
    b5-b4=1000
    Найти
    S5-


    Решение: Составим систему уравнений
    b(5)-b(3)=1200 (1)
    b(5)-b(4)=1000 (2) ⇒ b(5)= 1000+b(4) (2_2)
    Добавим в систему третье уравнение b(4)²=b(5)*b(3) (3)
    вычтем из уравнения (1)-(2) ⇒ b(4)-b(3)=200 ⇒ b(3)=b(4)-200 (4)
    Подставим (2_2) в (3)
     b(4)²=(1000+b(4))*b(3) Подставим вместо b(3) уравнение (4)
    b(4)²=(1000+b(4))*(b(4)-200)
    b(4)²==1000b(4)+b(4)²-200000-200b(4) [b(4)² сократим]
    800 b(4)=200000 b(4)=250
    b(3)=250-200=50  b(3)=50
    q=b(4)/b(3)=250/50=5 q=5
    b(3)=b(1)*q² ⇒ b(1)=50/25=2 b(1)=2
    S(5)= b(1)(q^n-1)/(q-1)
    S(5)=3125

<< < 12 3 > >>