найти наибольшее и наименьшее значение - страница 2
Найти наибольшее и наименьшее значение функции на отрезке.f(x)=3x2-x3, [-1;3]
Решение: f(x)=3x^2 - x^3, [-1;3]
Находим первую производную функции:
y’ = -3x2+6x
или
y’ = 3x(-x+2)
Приравниваем ее к нулю:
-3x2+6x = 0
x1 = 0
x2 = 2
Вычисляем значения функции
f(0) = 0
f(2) = 4
Ответ:
fmin = 0, fmax = 4
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y’’ = -6x+6
Вычисляем:
y’’(0) = 6>0 - значит точка x = 0 точка минимума функции.
y’’(2) = -6<0 - значит точка x = 2 точка максимума функции.Найти наибольшее и наименьшее значение функции на заданном промежутке: а)f(x)=x⁴ - 8x²- 3; x ∈ {-3;1} б)f(x) = sin x; x ∈ {0;π}
Решение: а)1.находим производную f(x)’=4x³-16x
2.приравниваем к нулю производную и решаем полученное уравнениеf(x)’=0 4x³-16x=0;
4x(x²-4)=04х=0 или x²-4=0
х=0 х=2 П.К.x=-2
3. находим f(x) f(0)=0⁴-8*0²-3=-3; f(-2)=(-2)⁴-8*(-2)²-3=-19; f(-3)=(-3)⁴-8*(-3)²-3=6f(1)=1⁴-8*1²-3=-10 наибольшее 6 наименьшее -19
Найти наибольшее и наименьшее значение на отрезке y = sin x-x-(x3(куб)/3), (0;П)
,
Решение: $$ y’=cosx-1-x^{2} $$
$$ cosx-1-x^{2}=0 $$
x=0
Если нарисовать рисунок этой функции то можно увидеть что эта функция убывает от нуля до П.
Таким образом наибольшая значение она принимает при х=0, а наименьшее при х=П
$$ y(0)=sin0-0-0=0 $$
$$ y( \pi )=sin \pi - \pi - \frac{\pi ^{3}}{3} =- \pi- \frac{\pi ^{3}}{3} $$
Наибольшее и наименьшее значения на отрезке функция достигает в точках экстремума или на концах отрезка. Найдём точки экстремума:
$$ y=sinx-x-\frac{x^3}{3},\\y’=cosx-1-x^2=0,\; \to \; \; cosx=1+x^2 $$
Так как $$ x^2 \geq 0,\; |cosx| \leq 1 $$ , то $$ cosx=1. $$
$$ cosx=1\; \to \; \; x=2\pi n,\; n\in Z $$
На отрезке $$ [0,\pi ] $$ экстремальной точкой будет х=0.
На концах отрезка функция принимает значения:
$$ y(0)=sin0-0-0=0,\\ y(\pi )=sin\pi -\pi -\frac{\pi ^3}{3}=-\pi (1+\frac{\pi ^2}{3})<0\\ \max\, y_{[0,\pi ]}=0\\min\, y_{[0,\pi ]}=-\pi (1+\frac{\pi ^2}{3}) $$Найти наибольшее и наименьшее значение функции y=x+4/x на отрезке 1; 4
Решение:y’=1-4/x^2
Найдем критические точки
1-4/х^2=0
x^2-4=0
x1=-2 не входит в отрезок от 1 до 4
x2=2
Считаем значение функции на концах отрезка и в критической точке, которая попадает в этот отрезок.
y(1)=1+4/1=5
y(2)=2+4/2=4
y(4)=4+4/4=5
наименьшее значение равно 4, а наибоьшее 5
Найти наибольшее и наименьшее значение функции f(x)=3x-x³ [-3;0]
Решение: F(x)=3x-x³
Находим производную
f ’ (x) = 3-3x²
Приравниваем у нулю 3-3х²=0 -3х²=-3 х²=1. х=1 х=-1 у нас дано промежуток (-3:0) +1 туда не входит
подставляем цифры эти в начало уравнения
f(-3)=-9+27=18
f(0)=0
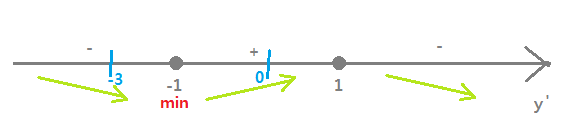
f(-1)=-3+1=-2 Наименьшее равно f(-1)= -2 min$$ f’(x)=3-3 x^{2} =0 \\ x^{2} =1 \\ x_1=1;x_2=-1 $$
Убывает от $$ x \un [-3;-1] $$
Возрастает на $$ x\in [-1;0] $$
Наибольшее значение $$ y_{max}(-3)=3(-3)-(-3)^3=-9+27=18 $$
Наименьшее значение $$ y_{min}(-1)=3*(-1)+1=-2 $$