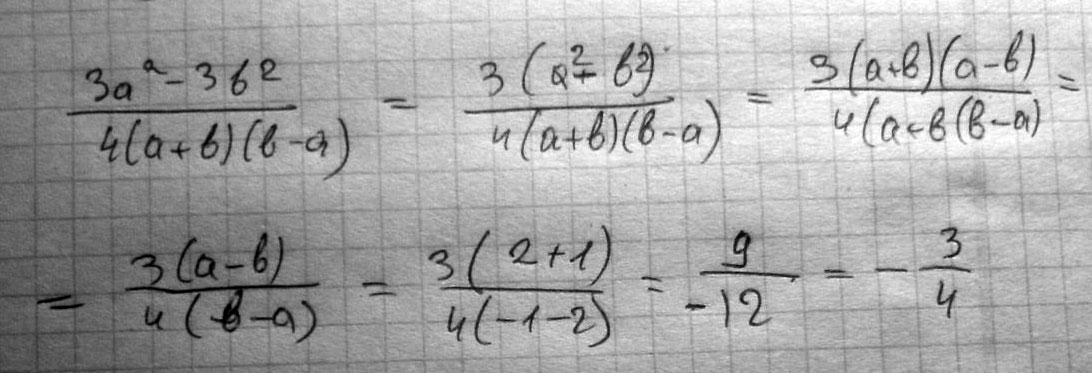найти значение »

значение алгебраического выражения

  • 1.Квадрат суммы; квадрат разности. Привести примеры.
    2.Найти значение алгебраического выражения 3а-2Ь при a= , b=1
    3.Правила раскрытия скобок и заключения в скобки. Привести примеры.
    4.Основные свойства уравнений. Привести примеры?


    Решение: 1.Докажем, что при любых значениях a и b верно равенство    (a+b) 2=a 2+b 2+2ab    или (a+b) 2=a 2+2ab+b 2.    Доказательство.    (a+b) 2=(a+b)(a+b)=a 2+ab+ab+b 2=a 2+b 2+2ab.  Если в эту формулу вместо a и b подставить какие-нибудь выражения,  то опять получится тождество.  Квадрат суммы двух выражений равен сумме квадратов этих выражений  плюс удвоенное произведение первого и второго выражений.    Докажем, что при любых значениях a и b верно равенство    (a−b) 2=a 2+b 2−2ab    или (a−b) 2=a 2−2ab+b 2.    Доказательство.    (a−b) 2=(a−b)(a−b)=a 2−ab−ab+b 2=a 2+b 2−2ab.  Квадрат разности двух выражений равен сумме квадратов этих выражений  минус удвоенное произведение первого и второго выражений.  2. a=2/3 3. Выражение а + (b + с) можно записать без скобок:    а + (b + с) = а + b + с.    Эту операцию называют раскрытием скобок.    Пример 1. Раскроем скобки в выражении а + ( – b + с).    Решение. а + ( –b + с) = а + ( (–b) + с ) = а + (–b) + с = а – b + с.    Если перед скобками стоит знак " + " , то можно опустить скобки  и этот знак " + " , сохранив знаки слагаемых, стоящих в скобках.  Если первое слагаемое в скобках записано без знака, то его надо  записать со знаком " + " .    – 2,87 + (2,87 – 1,5) = – 2,87 + 2,87 – 1,5 = 0 – 1,5 = – 1,5 .    Чтобы записать сумму, противоположную сумме нескольких  слагаемых, надо изменить знаки данных слагаемых:    – (а + b) = –a – b .    Обратите внимание, что отсутствие знака перед первым слагаемым  в скобках подразумевает знак "+" .    – ( а + b ) = – ( + а + b ) = – a – b .    Чтобы раскрыть скобки, перед которыми стоит знак " – " , надо  заменить этот знак на " + " , поменяв знаки всех слагаемых в скобках  на противоположные, а потом раскрыть скобки. 4. Основные свойства уравнений 1.В любой части уравнения можно приводить подобные слагаемые или раскрывать скобку. 2.Любой член уравнения можно переносить из одной части уравнения в другую, изменив его знак на противоположный. 3.Обе части уравнения можно умножать (делить) на одно и то же число, кроме 0.

  • Найдите значение алгебраического выражения (3a^2 - 3b^2)/(4(b+a)(b-a)), если a=2, b=-1


    Решение: Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий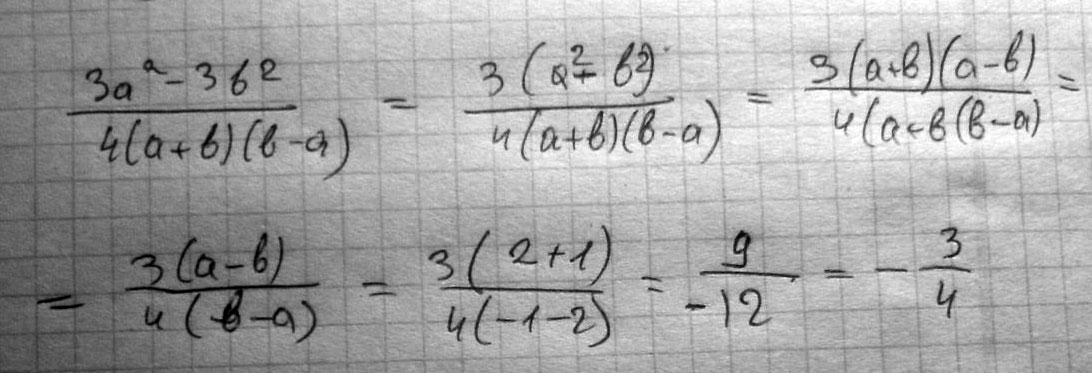Алгебраическим выражением называется одна или несколько алгебраических величин чисел и букв соединенных между собой знаками алгебраических действий...

  • Найдите значение алгебраического выражения: (7n+m)*(4m-n) при n= -3, m=2


    Решение: 1)Сначала упростим выражение:
    (7n+m)(4m-n)=28mn-7n²+4m²-mn=-7n²+27mn+4m²

    2)теперь подставим:
    -7*(-3)²+27*(-3)*2+4(2)²=-7*9-162+16=-63-162+16=-209
    Ответ: -209

    (7n+m)*(4m-n)
    раскрываем скобки, если перед скобками стоит знак + то мы остовляем всё как есть. А если перед скобками стоит знак минус, то все слагаемых меняем на противоположный знак.
    пишем: 7n+m+4m-n
    У нас подобные 7n и -n, m и 4m.
    дальше, 7n-n=6n, m+4m=5m
    получается 6n+5m
    Это мы упростили выражение.

    Теперь подставляем вместо n и m, -3 и 2
    6*(-3)+5*2= -18+10= -8
    Конец примера.

  • Найдите Значение Алгебраического Выражения: 1) \( 3a-2b \) при \( a= \frac{1}{3},b=1;a=0,01,b= \frac{1}{4} \)
    2) \( 2a+3b \) при \( a=3,b=-2;a=-1,4 ,b=-3,1 \)
    3) \( 0,25a-4c^2 \) при \( a=4,c=3;a=0,1,c= \frac{1}{2} \)
    4) \( 2a^2=- \frac{1}{3} b \) при \( a=2,b=9;a= \frac{1}{4} ,b=2,4 \)

    Сколько минут:
    1) в 7ч 30сек
    2) в M часах
    3) в P секундах
    4) в M часах,L минутах и P секундах


    Решение: 1)a=1/3;b=1  3*1/3-2*1=1-2=-1
    a=0,01;b=1/4  3*0,01-2*0,25=0,03-0,5=-0,47
    2)a=3;b=-2  2*3+3*(-2)=6-6=0
    a=-1;b=-3,1  2*(-1)+3*(-3,1)=-2-9,3=-11,3
    3)a=4;c=3  0,25*4-4*9=1-36=-35
    a=0,1;c=1/2  0,25*0,1-4*1/4=0,025-1=-0,975
    4)a=2;b=9  2*4-1/3*9=8-3=5
    a=1/4;b=2,4  2*1/16-1/3*2,4=1/8-0,8=0,125-0,8=-0,675

    1)7x30c=7*60+0,5=420,5мин
    2)mx=60*М мин
    3)Рс=Р/60 мин
    4)60М+L+P/60 мин

  • Найдите значение алгебраического выражения (15a + 8ab + 2b)/(3.5a - 1.5b) при a=2, b=0.4


    Решение: 15a +ab + 2b            8ab + 2                   8 × 2 × 0.4 + 2                     6.4
             ÷            =           ÷           =                      ÷                =             ÷      =  
            3.5                      3.5                               3.5                             3.5

    = 2.4

    Подставляем вместо переменных числовые значения:
    (15*2+8*2*0,4+2*0,4) / (3,5*2-1,5*0,4) = 37,2 / 1=37,2

1 2 > >>