Графический способ решения уравнения mx = n
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение не имеет корней.
Рассмотрим отдельно три случая.
-
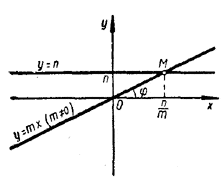m =/= 0. В этом случае графиком функции y = mx будет прямая, наклоненная к оси х под некоторым углом φ. Графиком функции у = n является прямая, параллельная оси х. Такие две прямые пересекаются и притом лишь в одной точке (точка М). Абсцисса точки пересечения, n/m , и есть корень уравнения mx = n. 
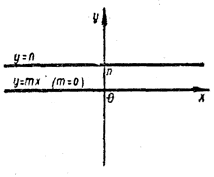m = 0, n =/= 0. В этом случае прямая у = mx сливается с осью х, а прямая у = n параллельна оси х. Прямые у = mx и у = n оказываются параллельными; точки пересечения таких прямых не существует. Поэтому не существует и корней уравнения mx = n.
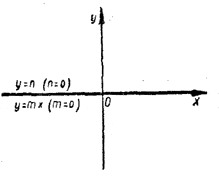m = n = 0. В этом случае прямые у = mx и у = n совпадают, сливаясь с осью х. О таких прямых можно сказать, что они пересекаются в каждой точке оси х. Поэтому в данном случае любое число является корнем уравнения mx = n.
m =/= 0. В этом случае графиком функции y = mx будет прямая, наклоненная к оси х под некоторым углом φ. Графиком функции у = n является прямая, параллельная оси х. Такие две прямые пересекаются и притом лишь в одной точке (точка М). Абсцисса точки пересечения, n/m , и есть корень уравнения mx = n.
m = 0, n =/= 0. В этом случае прямая у = mx сливается с осью х, а прямая у = n параллельна оси х. Прямые у = mx и у = n оказываются параллельными; точки пересечения таких прямых не существует. Поэтому не существует и корней уравнения mx = n.
m = n = 0. В этом случае прямые у = mx и у = n совпадают, сливаясь с осью х. О таких прямых можно сказать, что они пересекаются в каждой точке оси х. Поэтому в данном случае любое число является корнем уравнения mx = n.