решение уравнений »

найти действительные корни уравнения - страница 2

  • Уравнение х-2= с/х имеет два различных действительных корня, если С принадлежит множеству действительных чисел и выполняется условие C<1


    Решение: x-2=C/x, умножим левую и правую часть на x, получаем x^2-2*x=C, перенес С в левую часть x^2-2*x-C=0. Получаем квадратное уравнение, оно имеет два различных действительных корня если дискриминант больше 0.

     D=b^2-4*a*c, т.е D=4-4*1*C=4-4*C, 

    Решаем неравенство 4-4*С>0, получаем -4*С>-4, или 4*С<4, таким образом получаем что С<1.

    Ответ: Уравнение х-2=С/х имеет два действительных различных корня, если С принадлежит множеству действительных чисел и выполняется условие C<1

  • Найти все а, при которых уравнение x^5-5x+a=0 имеет два различных действительных корня


    Решение: 1)Для решения используем графическую интерпретацию. Количество решений уравнения f(x)=g(x) - это количество точек пересечения графиков y=f(x) и y=g(x).

    Запишем уравнение в виде ч$$ x^5=5x-a $$.

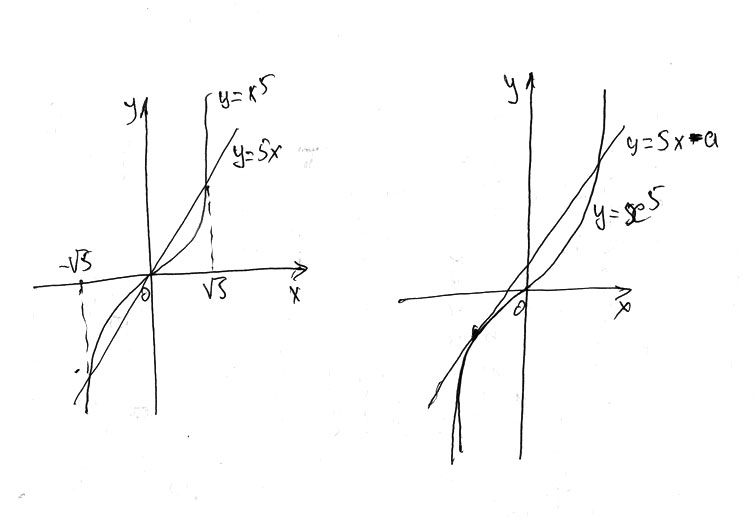
    2) При а=0 уравнение примет вид х⁵=5х, которое имеет три решения. (см рисунок).

    Если смещать прямую y=5x вдоль оси 0y можем получить две точки пересечения с графиком функции у=х⁵, если прямая y=5x-а будет касаться графика у=х⁵ (см рисунок). В этом случае и будет два решения. ( в остальных случаях либо 3 либо одна точка пересечения).

    3) По геометрическому смыслу производной в точке касания производная функции   у=х⁵ должна быть равна 5. $$ y’(x)=5x^4 $$ тогда $$ 5x^4=5 $$, тогда х=1 или х=-1.

    4) Уравнение касательной $$ y=y(x_{0})+y’(x_{0})(x-x_0) $$

    при х=1 у(1)=1; y’(1)=5 и уравнение касательной у=1+5(х-1), у=5х-4, тогда а=4.

    при х=-1 у(1)=-1; y’(1)=5 и уравнение касательной у=-1+5(х+1), у=5х+4, тогда а=-4.

    Ответ а=4 или а =-4

     Для решения используем графическую интерпретацию. Количество решений уравнения f x g x - это количество точек пересечения графиков y f x и y g x . Запишем уравнение в виде ч...

  • Найти действительные корни уравнения:

    2х4+3х3-10х2-5х-6=0


    Решение: Данное уравнение раскладывается на множители :
    (x-2)(x+3)(2x^2+x+1)=0
    т.е.
    x-2=0 or x+3=0 or 2x^2+x+1=0
    x=2 x=-3 не существует в множестве вещественных чисел
    Ответ -3;2

  • Найти действительные корни уравнения (2x^2-1)^2+x(2x-1)^2=(x+1)^2+16x^2-6


    Решение: $$ (2x^2-1)^2+x(2x-1)^2=(x+1)^2+16x^2-6 $$
    Перенесем в левую часть и раскрываем скобки
    $$ x(2x-1)^2+(-(x+1)^2-16x^2+6+(2x^2-1)^2)=0 $$
    $$ x(2x-1)^2+(-x^2-2x-1-16x^2+6+4x^4-4x^2+1)=0 \\ x(2x-1)^2+(-21x^2-2x+6+4x^4)=0 \\ x(2x-1)^2+(2x-1)(2x^3+x^2-10x-6)=0 \\ (2x-1)(2x^3+3x^2-11x-6)=0 $$
    Произведение равно нулю
    $$ 2x-1=0 \\ 2x=1 \\ x=1:2 \\ x_1=0.5 $$
    $$ 2x^3+3x^2-11x-6=0 $$
    Решаем методом разложение на множители
    $$ 2x^3-4x^2+7x^2-14x+3x-6=0 \\ 2x^2(x-2)+7x(x-2)+3(x-2)=0 \\ (x-2)(2x^2+7x+3)=0 $$
    Каждое произведение равно нулю
    $$ x-2=0 \\ x_2=2 $$
    $$ 2x^2+7x+3=0 $$
    Находим дискриминант
    $$ D=b^2-4ac=7^2-4\cdot2\cdot3=25 $$
    Воспользуемся формулой корней квадратного уравнения
    $$x_3,_4= \frac{-b \pm \sqrt{D}}{2a}$$
    $$ x_3=-3 \\ x_4=-0.5 $$

    Ответ: $$ -3;\,\,-0.5;\,\,0.5;\,\,2 $$

  • найти действительные корни уравнения:

    x^2(x-2)(6x+1)+x(5x+3)=1


    Решение: действиетльные это объединение рациональных и иррациональных чисел
     расскрываем скобки

    x^2(6x^2-12x+x-2)+5x^2+3x-1=0

    6x^4-11x^3-2x^2+5X^2+3x-1=0

    6x^4-11x^3+3x^2+3x-1=0

    дальше делим уголком

    ответ 6х^3-5x^2-2x+1 еще раз делим

    получаем 6х^2+x-1 ну а дальше решаем как обычное квадратное уравнение, уголком делить надо на х-1

<< < 12 3 4 > >>