найти действительные корни уравнения - страница 4

Найти значения а, при которых уравнение имеет действительный решение и указать знаки корней: $$ x^{2} -2(a-1)x+2a+1=0 $$

X^2-2(a-1)x+2a+1=0 чтобы уравнение имело 1 действительное решение дискриминант должен быть равен 0,
D=0 
D(половинный)=(a-1)^2-2a-1=a^2-2a+1-2a-1=a^2-4a
a^2-4a=0
a(a-4)=0
a=0 a=4
x^2+2x+1=0 x^2-6x+9=0
(x+1)^2=0 x=-1 отрицателен (x-3)^2=0 x=2 положителен

Вариант решения 2: X^2 - 2(a-1)x + (2a+1) = 0
1) Если оно имеет действительные корни, то D >= 0
D/4 = (b/2)^2 - ac = (a-1)^2 - 1(2a+1) = a^2 - 2a + 1 - 2a - 1 = a^2 - 4a >= 0
a(a - 4) >= 0
a <= 0 U a >= 4

Знаки корней.
2) Если a <= 0, то a - 1 < 0
x1 = (-b/2 - √(D/4)) / a = (a - 1 - √(a^2 - 4a)) / 1 = a - 1 - √(a^2 - 4a) < 0
x2 = (-b/2 + √(D/4)) / a = (a - 1 + √(a^2 - 4a)) / 1 = a - 1 + √(a^2 - 4a)
x2 может быть и больше и меньше 0.
a) a - 1 + √(a^2 - 4a) < 0
√(a^2 - 4a) < 1 - a
a^2 - 4a < a^2 - 2a + 1
2a > -1;
-1/2 < a <= 0
b) a - 1 + √(a^2 - 4a) > 0
Аналогично получаем
a < -1/2

3) Если a = -1/2, то c = 2a + 1 = 0, тогда
x^2 - 2(-1/2 + 1)x + 0 = 0
x^2 - 2(1/2)x = 0
x^2 - x = 0
x1 = 0, x2 = 1 > 0

4) Если a >= 4, то a - 1 > 0
x1 = (-b/2 - √(D/4)) / a = (a - 1 - √(a^2 - 4a)) / 1 = a - 1 - √(a^2 - 4a)
x1 может быть и больше и меньше 0.
x2 = (-b/2 + √(D/4)) / a = (a - 1 + √(a^2 - 4a)) / 1 = a - 1 + √(a^2 - 4a) > 0
a) a - 1 - √(a^2 - 4a) < 0
√(a^2 - 4a) > a - 1
a^2 - 4a > a^2 - 2a + 1
2a < -1
a < -1/2 - не подходит, потому что a >= 4
b) a - 1 - √(a^2 - 4a) >= 0
√(a^2 - 4a) <= a - 1
a^2 - 4a <= a^2 - 2a + 1
2a >= -1
a >= -1/2 - подходит для любых a >= 4
Значит, при любом a >= 4 оба корня положительны.
Ответ: При -1/2 < a <= 0 будет x1 < 0, x2 < 0
При a = -1/2 будет x1 = 0, x2 > 0
При a < -1/2 будет x1 < 0, x2 > 0
При a >= 4 будет x1 > 0, x2 > 0
При 0 < a < 4 действительных корней нет.

a) √5x+8=6,где под знаком корня все выражения( 5x+8)
б) √X²-4x+13=5, где под знаком корня выражение (x в квадрате-4x+13)
в) (√x²-4) - √8x+5=0, где под первым знаком корня выражение( x в квадрате -4), а под вторым знаком корня (8x+5)
г) √2x²-5x+1=x-1, где под знаком корня выражение( 2x в квадрате-5x+1).

Пусть уравнение x² + px + q = 0 имеет два действительных корня x₁ и x₂. Записать приведенное квадратное уравнение, имеющее корни -x₁ и - x₂.

$$ x_1+x_2=-p; $$

$$ x_1*x_2=q. $$

Если корни те же по модулю но противоположного знака, то соотношения для новых p и q будут следующие:

$$ -x_1-x_2=-p_1; $$

$$ (-x_1)*(-x_2)=q_2. $$

Отсюда видим, что:

$$ p_1=-p;\ \ \ \ q_1=q. $$

Тогда приведенное квадр. ур-ие будет выглядеть так:

$$ x^2-px+q=0. $$

2cos^2х+7sinx-5=0 и укажите корни,удовлетворяющие условию cosх ≤0

2(1-sin²x)+7sinx-5=0

2-2sin²x+7sinx-5=0

2sin²x-7sinx+3=0

замена sinx=t

2t²-7t+3=0

D=49-24=25

t₁=3 sinx≠3 - решений нет

t₂=1/2 sinx=1/2

  x=(-1)^n · π/6 + πn, n∈Z

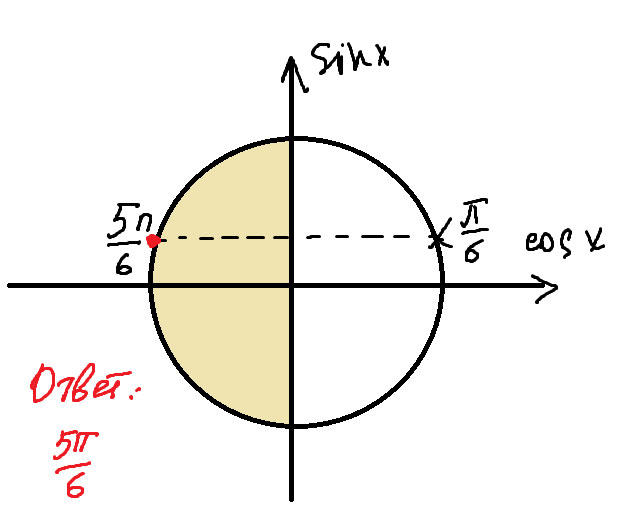
+ отбор на рис.

корни, удовлетворяющие условию cosх ≤0

$$ 2cos^{2}x+7sinx-5=0\\2(1-sin^{2}x)+7sinx-5=0\\-2sin^{2}x+7sinx-3=0\\sinx=t\\-2t^{2}+7t-3=0\\ D=49-4\cdot(-2)\cdot (-3)=25; \\x_{1,2}=\frac{-7\pm \sqrt{25}}{2\cdot (-2)}\\x_{1}=\frac{-7+ 5}{-4}=\frac{1}{2},\\x_{2}=\frac{-7-5}{-4}=3;\\sinx=\frac{1}{2}\\x=(-1)^{n}arcsin \frac{1}{2}+\pi n, n\in Z,\\ x=(-1)^{n}\frac{\pi}{6}+\pi n, n\in Z, \\cosx\leq 0,\\ x=\pi -\frac{\pi}{6}+2 \pi n=\frac{5 \pi}{6}+2 \pi n, n \in Z\\sinx=3 \varnothing $$

Ответ: $$ x= \frac{5 \pi}{6}+2 \pi n, n \in Z $$

Найти корни уравнения x^3+3x^2-6x+a=0, если известно, что оно имеет три различных действительных корня, образующих геометрическую прогрессию.