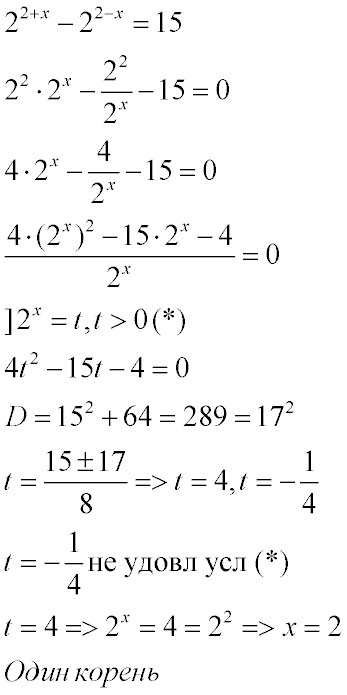решение уравнений »

число корней уравнения

  • Число корней уравнения ctg(2х + 120) = корень из 3 на 3, принадлежащих промежутку (-180;270], равно

    A) 0

    B) 5

    C) 1

    D) 4


    Решение:

    Ctg(2x + 120) = √3/3
    ctg(2x + 2π/3) = √3/3
    2x + 2π/3 = π/3 + πk, k∈Z
    2x = π/3 - 2π/3 + πk = -π/3 + πk, k∈Z
    x = -π/6 + πk/2, k∈Z
    x∈(-π; 3π/2]
    -π < -π/6 + πk/2 ≤ 3π/2
    -π + π/6 < πk/2 ≤ 3π/2 + π/6
    -5/3 < k ≤ 10/3, k∈Z
    k = -1, 0, 1, 2, 3 - значит указанному промежутку принадлежит ПЯТЬ корней.

    k = 0, x1 = -π/6 = -30 градусов
    k = -1, x2 = -π/6 - π/2 = -2π/3 = -120градусов
    k =  1, x = -π/6 + π/2 = π/3 = 60градусов
    k = 2, x = -π/6 + π = 5π/6 = 150градусов
    k = 3, x = -π/6 + 3π/2 = 8π/6 = 4π/3 = 240градусов

    Ответ: В) 5 корней 

  • Число корней уравнения равно \( 2^{2+x}-2^{2-x}=15 \)


    Решение: $$ 2^{2+x} - 2^{2-x} =15 $$
    $$ 2^{2} * 2^{x} - \frac{ 2^{2} }{ 2^{x} } =15 $$
    $$ 2^{x} = t $$
    $$ 4t^{2} - 15^{t} - 4 = 0 $$
    D=225+64=289, $$ \sqrt{289} =17 $$
    $$ t1= \frac{15-17}{8} = -\frac{1}{4} $$
    $$ t2= \frac{15+17}{8}=4 $$
    $$ 2^{x} = -\frac{1}{4} $$-не подходит;
    $$ 2^{x} =4 $$
    x=2
    Ответ:2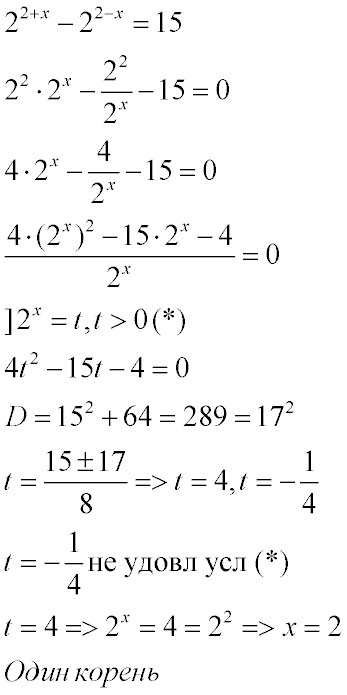

    x - -x x - frac x x t t - t - D sqrt t frac - - frac t frac x - frac -не подходит x x Ответ...

  • Число корней уравнения равно: \( \sqrt{4x+\sqrt{16+17x^{2}}}=x+2 \)


    Решение: Выражение под корнем должно быть больше или равно нуля. Кроме того, значение корня всегда больше или равно нуля. Таким образом:

    x+2≥0 (значение корня)

    x≥-2

    16+17x²≥0 (выражение под корнем)

    17x²≥-16

    x²≥-16/17

    x∈R

    4x+√(16+17x²)≥0 (выражение под корнем)

    √(16+17x²) всегда ≥0 ⇒ 4x≥0

    x≥0

    x≥-2 ∧ x∈R ∧ x≥0 <-- назначаем общей часть промежутков

    ОДЗ∈<0,∞)

    4x+√(16+17x²)=(x+2)²

    √(16+17x²)=x²+4x+4-4x

    √(16+17x²)=x²+4

    16+17x²=(x²+4)²

    16+17x²=x⁴+8x²+16

    x⁴-9x²=0

    x²(x²-9)=0

    x²(x-3)(x+3)=0

    x=0 ∨ x=3 ∨ x=-3

    -3∉ОДЗ

    x=0 ∨ x=3

  • Число корней уравнения \( cos^2x+3sin^2x-1=\sqrt{3}sin2x \) на отрезке \( [\frac{\pi}{2};\pi] \) равно?


    Решение: (cos²x+sin²x)+2sin²x-1=√3(2sinx cosx)

    1+2sin²x-1=2√3sinx cosx

    2sin²x-2√3sinx cosx=0

    2sinx(sinx-√3cosx)=0

    1) sinx=0, x=πn, n∈Z ⇒ n=0,x=0

    n=1, x=π∈[π/2,π]

    2) sinx-√3cosx=0 Делим на cosx≠0

    tgx=√3, x=π/3+πk, k∈Z ⇒ k=0, x=π/3

    k=1, x=4π/3

    k=-1, x=-2π/3 ...

    Ответ: корень из сегмента [π/2, π] - это х=π.

  • Определите число корней уравнения -х2+4x+5=0


    Решение: Два корня уравнения. Это:
    x1=-5
    x2=1

    A= -1, b= 4, c= 5 - ЧИСЛА ВЗЯТЫ ИЗ ВАШЕГО УРАВНЕНИЯ!
    Формула дискриминанта следующая D=(b)2 ( b в квадрате) - 4*a*c.
    Получается, D=(4)2 - 4*(-1)*5= 16+25= 36.
    Чтобы найти корни уравнения понадобится формула, которую можете увидеть на картинке. Корень из 36 = 6.
    Получается, Х1=-4+6/ 2*(-1) = 2/-2= -1.
    Находим Х2=-4-6/2*(-1) = -10/-2 = -5.
    Корни уравнения равняются -1 и -5.

1 2 3 > >>