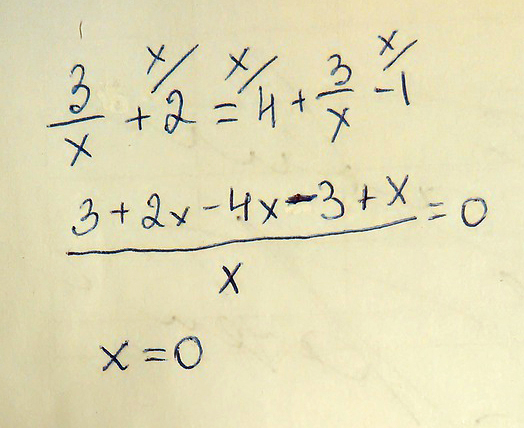решение уравнений »
дробное рациональное уравнение - страница 2
Дробные рациональные уравнения
3/x+2=4+3/x-1
Решение:
решить уравнение: 3/(x+2) = 4+3/(x-1)3/(x+2) = 4+3/(x-1) ОДЗ: x+2 ≠ 0 и x-1 ≠ 0 x ≠ - 2 и x ≠ 13/(x+2) = 4 + 3/(x-1) | *(x+2)*(x-1)3*(x-1) = 4*(x+2)*(x-1) + 3 *(x+2)3х - 3 = 4(х² -х + 2х -2) + 3х + 63х - 3 = 4(х² + х - 2) + 3х + 63х - 3 = 4х² + 4х - 8 + 3х + 63х - 3 = 4х² + 7х - 2 4х² + 7х - 2 - 3х + 3 = 0 4х² + 4х + 1 = 0D = 16 - 4*4 16 -16 = 0х₁ = х₂ = - 4/8 = - 1/2 (удовлетворяет ОДЗ) Ответ: - 1/2. Упростим выражение:3/(x+2)=7/(x-1) Составим пропорцию:7(x+2)=3(x-1)7x+14=3x-34x=-17x=-17/4x= -4 1/4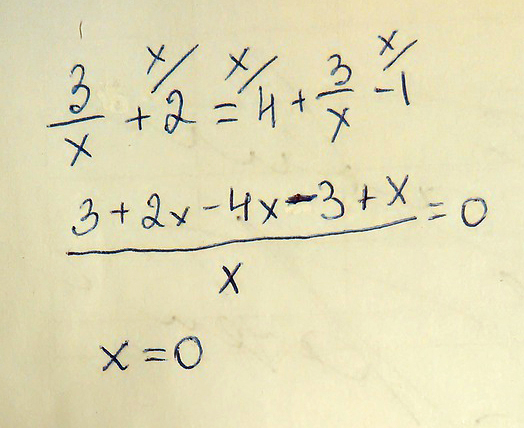
Решите дробно-рациональные уравнения
1) 1/x-5 - 1/x = 1, в ответе укажите сумму корней.
2) x -2= 4x-14/x-3
3)4/x^2 +4 + 5 / x^2 - 5 =2
4) 3- 7x/ 2x+4 = 1,5 - 3,5x / x+2
5) x/x+1 + x+1/x+2 + x+2/x =3
Решение: 1) $$ \frac{1}{x-5} - \frac{1}{x}=1 $$
Общ. знам.: x (x-5) ≠0
x - (x-5) = x(x-5)
x - x + 5 = x² - 5x
x² - 5x - 5 = 0
D = 25 + 20 = 45
x₁ = $$ \frac{5+ \sqrt{45} }{2} $$
x₂= $$ \frac{5- \sqrt{45} }{2} $$
x₁ + x₂ = $$ \frac{5+ \sqrt{45} }{2} + \frac{5- \sqrt{45} }{2} = \frac{5+ \sqrt{45}+5- \sqrt{45} }{2} = \frac{10}{2} =5 $$
Ответ: 5
2) $$ x-2= \frac{4x-14}{x-3} $$
Общ. знам.: x-3≠0
(x-2)(x-3) = 4x-14
x² - 3x - 2x + 6 = 4x - 14
x² - 9x + 20 = 0
D = 81-80=1
x₁ = (9+1) /2 = 5
x₂ = (9-1) / 2 = 4
Ответ: 5; 4
3) $$ \frac{4}{ x^{2} +4} + \frac{5}{ x^{2} -5}=2 $$
Общ. знам.: (x² + 4)(x² - 5) ≠ 0
4(x²-5) + 5(x²+ 4) = 2(x² +4) (x²-5)
4x² - 20 + 5x² + 20 = 2x⁴ - 10x² + 8x² - 40
2x⁴ -11x² - 40 = 0
x² = t; t≥0
2t² - 11t - 40 = 0
D = 121 + 320 = 441
t₁ = (11+21) / 4 = 8
t₂ = (11-21) / 4 = -2.5 не удов. усл.: t≥0
x² = 8
x₁ = $$ \sqrt{8}=2 \sqrt{2} $$
x₂ = $$ -2 \sqrt{2} $$
Ответ: $$ 2 \sqrt{2} ;-2 \sqrt{2} $$
4) $$ \frac{3-7x}{2x+4}= \frac{1.5-3.5x}{x+2} \\ \frac{3-7x}{2(x+2)} = \frac{1.5-3.5x}{x+2} $$
Общ. знам.: 2(x+2) ≠ 0
3-7x = 2*(1.5-3.5x)
3 - 7x = 3 - 7x
0 = 0
x - любое, НО 2(x+2)≠0 ⇒ x≠-2
x∈ (-беск.; -2) U (-2; +беск.)
Ответ: (-беск.; -2) U (-2; +беск.)
5) $$ \frac{x}{x+1}+ \frac{x+1}{x+2}+ \frac{x+2}{x}=3 $$
Общ. знам.: x (x+1)(x+2) ≠ 0
x*x(x+2) + (x+1)(x+1)*x + (x+2)*(x+1)*(x+2) = 3x(x+1)(x+2)
x³ + 2x² + x*(x+1)² + (x+1)(x+2)² = 3x (x² + 2x + x + 2)
x³ + 2x² + x (x² + 2x + 1) + (x+1)(x²+4x+4) = 3x³ + 9x² + 6x
x³ + 2x² +x³ + 2x² +x + x³ + 4x² + 4x + x² + 4x+ 4 = 3x³ + 9x² + 6x
3x³ + 9x² +9x + 4 = 3x³ + 9x² + 6x
3x = -4
x = $$ - \frac{4}{3} =-1 \frac{1}{3} $$
Ответ: $$ -1 \frac{1}{3} $$Решите дробные рациональные уравнения. \(\frac{x^2-6}{x-3}=\frac{x}{x-3}\)
\(\frac{x-4}{x}=\frac{2x+10}{x+4}\)
Решение: 1) 2 дроби равны, если равны их числители и знаменатели следовательно x^2-6=x
ОДЗ х не равен 3. x^2-x-6=0 Дискриминант= 1+4*6=25=5^2
x1=(1+5)/2=3 x2=(1-5)/2=-2 корень 3 не соответствует ОДЗ сл-но Ответ:-2
2) по св-ву пропорций имеем (х-4)(х+4)=х(2х+10) ОДЗ х не равен 0 х не равен -4
х^2-16=2x^2+10x x^2+10x+16=0 Дискриминант= 10^2-4*16=100-64=36=6^2
x1=(-10+6)/2=-2 x2=(-10-6)/2=-4 -4 не удовлетворяет ОДЗ Ответ-2Решить дробно рациональные уравнения
x/(x+2)+(x+2)/(x-2)=8/(x^2-4)
3x/(3-x)+9/(x-2)=x
1/(2-x)-1=(6-x)/(3x^2-12)
Решение: 1) Разложить знаменатель правой части уравнения на множители
x\(x+2)+(x+2)\(x-2)=8/((x-2)(x+2))
привести к общему знаменателю и перенести правую часть уравнения в левую
(x(x-2) +(x+2)^2-8)/((x-2)(x+2))=0
Отбрасываем знаменатель, раскрываем скобки и решаем получившееся квадратное уравнение
(x+2)^2+x(x-2)-8=0
x^2+2x+42x^2-2x-8=0
2x^2-4=0
x^2=2
x=+-(корень)2Решите дробные рациональные уравнения
\( \frac{x^{2}-12}{x-3} = \frac{x}{3-x} \)
\( \frac{2x^{2}-5x+2}{x-2} = 4x+1 \)
Решение: x²-12 x- = - ОДЗ: х≠3
x-3 x-3
х²-12+х =0, (х+4)(х-3)=0, х=-4, х=3 - не входит в ОДЗ
Ответ: х=-4
2) ОДЗ: х≠2
2х²-5х+2=(х-2)(4х+1)
2х²-5х+2=4х²-8х+х-2
2х²-2х-4=0, х²-х-2=0 Корни по теореме Виета равны х=-1 или х=2 - не входит в ОДЗ
Ответ: х=-1