корни »
при каких значениях уравнение не имеет корней
С какими значениями параметра "a" у уравнения нету действительных корней?ax^2-(a+1)x+2a-1=0
Решение: Когда дискриминант меньше нуля.
Находим D:
D=(a+1)^2-4*a*(2a-1)=
=a^2+2a+1-8a^2+4a=-7a^2+6a+1.
Находим дискриминант дискриминанта, решаем ур-е.
D=36+28=64=8^2
a1=-6+8-14=-17
a1=-6-8-14=1
Ур-е:
-7(a+17)(a-1).
Методом интервала находим, когда меньше нуля:
От -бесконечности до -17 и от 1 до бесконечности.При каких значениях m уравнение 2x^2+mx+2=0 не имеет действительных корней
Решение: Уравнение не имеет корней, если дискриминант меньше 0, значит:
D=b²-4ac
D=b²-4*2*2=b²-16
т.к. квадрат любого числа всегда положительный, то дискриминант будет отрицательный при m∈(-4;4)
Ответ: уравнение корней не имеет при m∈(-4;4)Квадратное уравнение не имеет действительных корней если дискриминант меньше 0
2x²+mx+2=0
D=m²-4*2*2=m²-16
m²-16<0
m²=16
m=4 m=-4
+ - +
---------------------(-4)-----------------------(4)-----------------------
m∈(-4;4)При каком значении параметра α уравнения имеет три различных действительных корня |2x²-5x+3|=α
Решение: График функции - парабола, отраженная относительно оси х, у=а, прямая параллельная оси х, три точки пересечения возможны только при а=1/8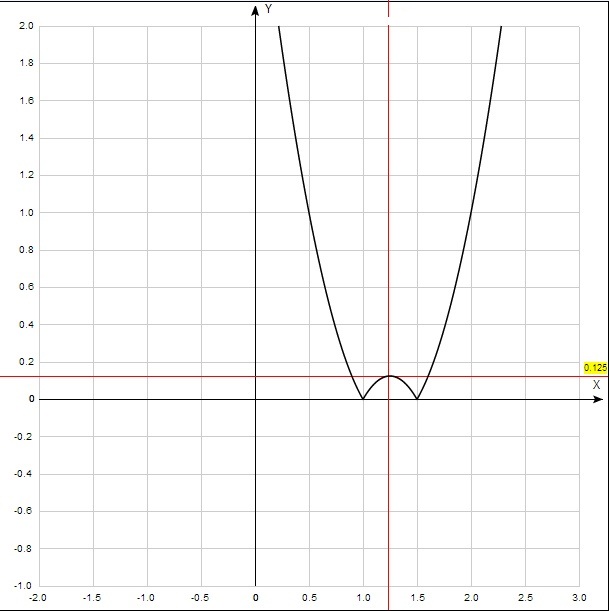
Уравнение |2-3x-x^2|=5a имеет три различных действительных корня. Каково значение а ?
Решение: Равносильно совокупности : 2-3x-x^2=+-5a При этом a>=0 3 корня возможно лите когда 1 уравнение имеет 1 корень а другое два или наоборот. 1) положим, что второе имеет один корень: x^2+3x-5a-2=0 9-4*(-5a-2)=0 Невозможно, т.к. a>0, проверим второе: x^2+3x+5a-2=0 9-4*(5a-2)=0 5a-2=9/4 a=17/4 Подставив его в дискриминант первого уравнения сразу очевидно, что он положительный. То есть у него будет два корня. А в итоге 3 ответ:17/4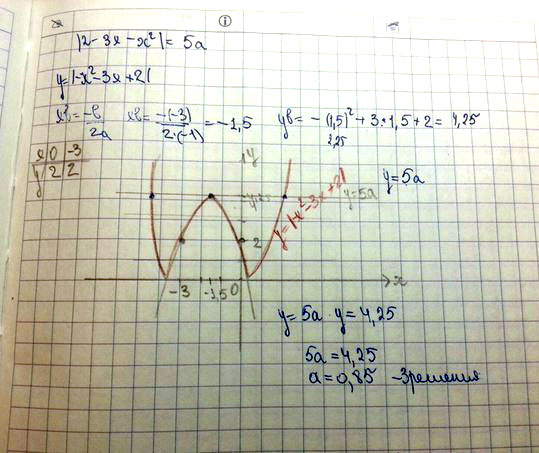
При каких значениях n квадратное уравнение x^2 + 2nx + 4 = 0 имеет два различных действительных корня?
Решение: Начнем с того, что это уравнение квадратное. Квадратное уравнение имеет два различных действительных корня при условии, что дискриминант больше 0, т.е когда дискриминант положителен. Дискриминант (D) вычисляется по формуле D=b^2-4ac где a b и c - коэффициенты. Значит мы должны найти такое n, когда неравенство b^2-4ac>0 - действительно.
Подставим заданные значения a b и c в неравенство:
(2n)^2-4*1*4>0
4n^2-16>0
4n^2>16
n^2>4
n> +/- 2
Отметим точки -2 и 2 на координатной прямой и узнаем в каких из интервалов (-∞;-2); (-2;2); (2;+ ∞) значение дискриминанта положительное.
Получаем соответственные знаки + - +, значит искомые интервалы (со знаком +) это (-∞;-2);(2;+ ∞). Эти интервалы и будут ответами.


