при каких значениях уравнение не имеет корней - страница 5
При каких значениях параметра а уравнение имеет два различных натуральных корня.
ax^2-(2a^2+5)x+10a=0
1. если а=0,то 0*x^2-(2*0+5)x+10*0=0. -5x=0 x=0, при а=0 уравнение имеет 1 корень, не удов решению задачи. Если а не равно 0, то уравнение квадратное имеет 2 корня, если d>0 D=(2а^2+5)^2-4*a*10а=4a^2+25-2а^2
Решение: Чтобы уравнение имело два корня, дискриминант должен быть больше нуля:
$$ D=(2a^2+5)^2-4*10a*a=4a^4+20a^2+25-40a^2 = 4a^4-20a^2+25 $$ $$ = (2a^2-5)^2 $$. И вот эта вот штука должна быть строго больше нуля. Но так как это квадрат какого то числа, то она всегда будет положительна или равна нулю. А когда дискриминант равен нулю, уравнение будет иметь одно решение. Значит:
$$ 2a^2-5 eq 0, a^2 eq \frac{5}{2}, a eq \frac{+}{-} \sqrt{ \frac{5}{2} } $$
Ну и плюс, что а не равно нулю.
То есть подходят все числа кроме 0 и $$ \frac{+}{-} \sqrt[]{ \frac{5}{2} } $$При каких значениях параметра a уравнение 4/3*x^3-4x+3=a имеет более одного корня?
Решение: Конечно такие задачи имеют какой-то определенный алгоритм через экстремум, но4x^3/3-4x=0
4x^3=12x
4x^2=12
x^2=3
x=+-V3
то есть при а=3 имеет уже 2 корня, посмотрим что будет при а=1
4/3*x^3-4x+3=1
4x^3-12x+9=3
4x^3-12x+6=0
2x^3-6x+3=0
имеет 3 корня
а при а =0 не имеет решений вообще
Сделаем вывод: при a>0
Какие будут значения х1 и х2 в уравнениях: х^-6х+1=0, х^-6х-1, х^-6х+2, х^-6х+4.
Возможные ответы: х1,2=3+-√5; 3+-√10, 3+-2√2 ; 3+-√11 ;3+-√7
Решение: X² - 6x + 1 = 0
D = b² -4ac = 36 - 4 × 1 = 32
x1,2 = 6+/-√32/ 2
x² - 6x + 2 = 0
D = 36 - 4 × 2 = 36 - 8 = 28
x1,2 = 6+/-√28/2
x² - 6x + 4 = 0
D = 36 - 4×4 = 36 - 16 = 20
x1,2 = 6+/-√20/2
X²-6x+1=0
D= 6²-4*1*1= 36-4=32
х= (6 +- √32) /2= 3 +- √ 8= 3+-2√2
x²-6x-1=0
D= 36+4= 40
х=(6+- √40) /2 = 3 +-√10
х²-6х+2=0
D= 36-8= 28
x= (6+-√28)/2= 3+-√7
x²-6x+4=0
D= 36-16= 20
x= (6 +-√20)/2 = 3 +- √5
При каких значениях k уравнение 3xво 2 степени +kx+1=0 не имеет корней? Приведите пример отрицательного значения k, при котором выполняется это условие.
Решение: Корней нет, когда дискриминант отрицательный (хотя там корни есть, но только они комплексные)Это обычное квадратное уравнение, оно не имеет корней, когда дискриминант строго меньше нуля, следовательно 3х^2+кх+1=0 Д=k^2-12 K^2-12<0 k^2<12 k<(12) ( ( ) - корень ) При К < корня из 12 уравнение не имеет корней. Тут получается любое отрицательное число, например -1
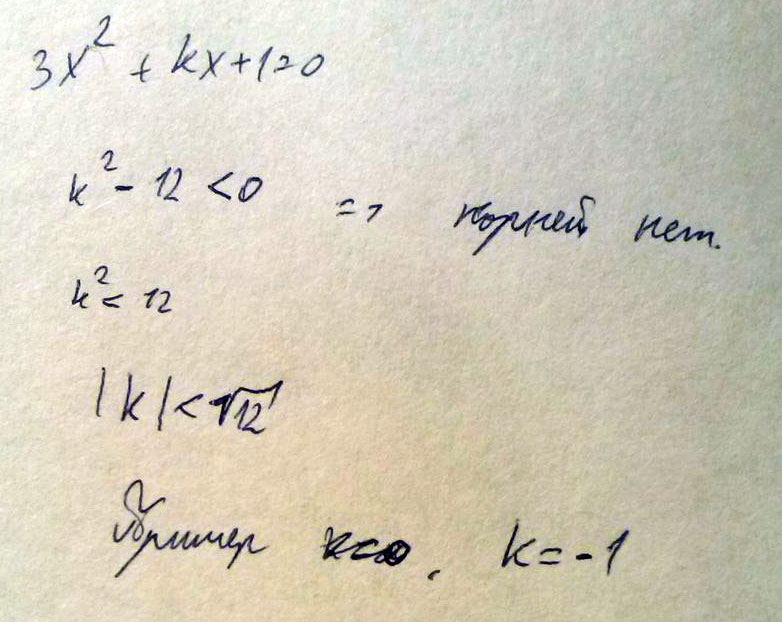
При каких значениях k уравнение 3x^2 +kx+1=0 не имеет корней? Приведите пример отрицательного значения k, при котором выполняется это условие.
Решение: Это обычное квадратное уравнение, оно не имеет корней, когда дискриминант строго меньше нуля, следовательно3х^2+кх+1=0
Д=k^2-12
K^2-12<0
k^2<12
k<(12) ( ( ) - корень )
При К < корня из 12 уравнение не имеет корней.
Тут получается любое отрицательное число, например -1