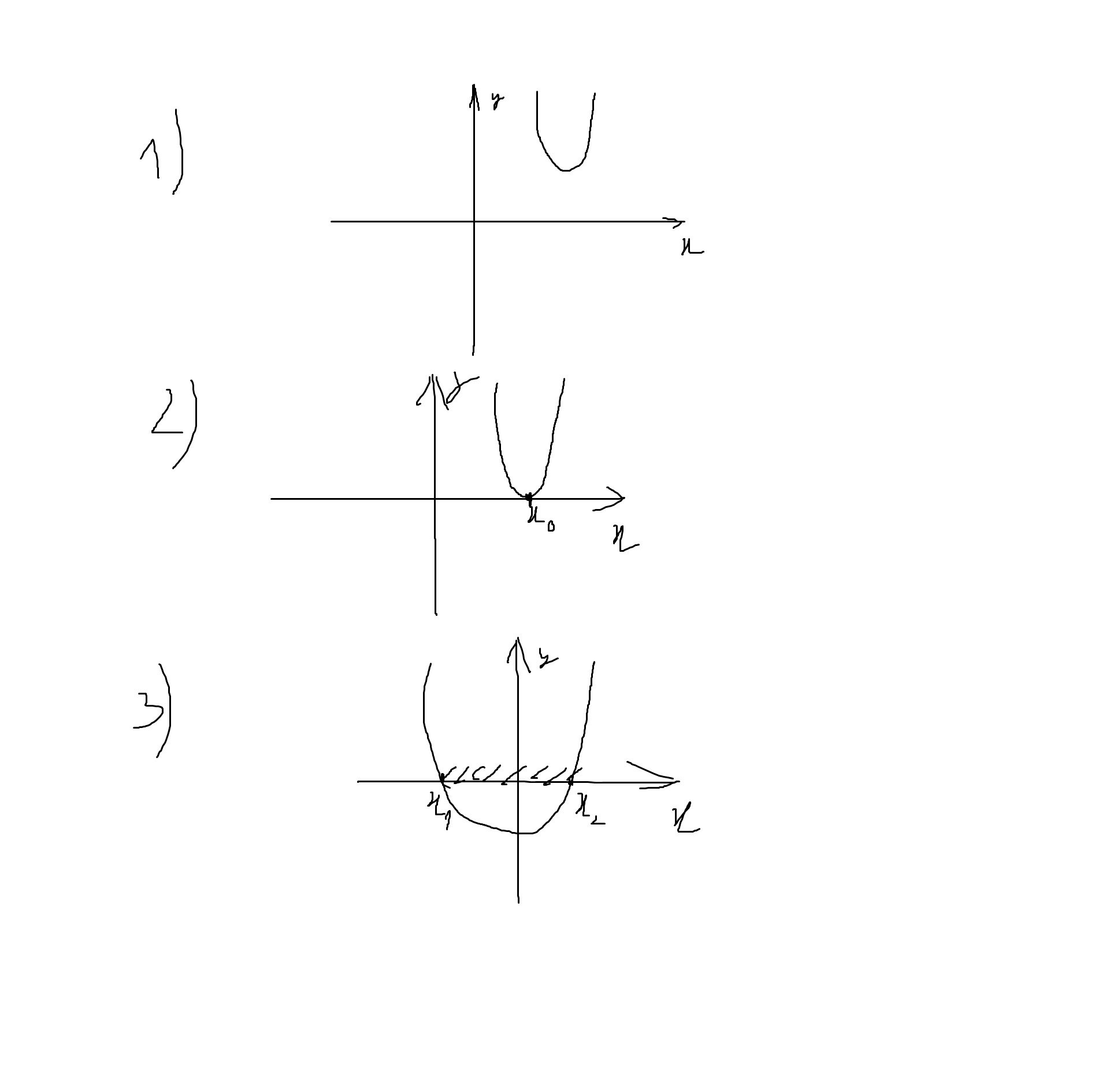упростите выражение
1. Найдите значение числового выражения:(2/7 + 3/14)(7,5 – 13,5)
2. Упростите выражение:
а) 5а – 3b – 8а + 12 b
б) 16с + (3с – 2) – (5с + 7)
в) 7 – 3(6y – 4)
3. Сравните значения выражений 0,5х – 4 и 0,6х – 3 при х = 5
4. Упростите выражение 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при х = ⅔
5. В прямоугольном листе жести со сторонами х см и y см вырезали квадратное отверстие со стороной 5 см. Найдите площадь оставшейся части. Решите задачу при х = 13, y = 22.
Решение: 1) (2/7 + 3/14)(7,5 – 13,5) = (4/14 + 3/14)* (-6) = -7*6/14 = -7*3/7 = -3
2) 5а – 3b – 8а + 12 b = -3a + 9b = 3(3b - a)
16с + (3с – 2) – (5с + 7) = 16c + 3c - 2 - 5c - 7 = 14c - 9
7 – 3(6y – 4) = 7 - 18y + 12 = 19 - 18y
3)0.5*5 -4 = 2.5 - 4 = -1.5
0.6*5 - 3 = 3 - 3 = 0
-1.5 < 0
4) 6,3х – 4 – 3(7,2х + 0,3) = 6.3x - 4 - 21.6x - 0.9 = -15.3x - 4.9
-15.3 * 2/3 - 4.9 = -15.1
5) площадь всего листа = 13*22 = 286
площадь вырезанного = 5*5 = 25
площадь оставшейся части = 286 - 25 = 261№ 1
( 2 + 3 ) (7,5-13,5) = 7/14 ×6 = 3
7 14
№ 2
а) 5а-3в-8а+12в = 9в-3а = 3(3в-а)
б) 16с+(3с-2)-(5с+7) = 16с+3с-2 -5с-7= 14с-9
в) 7-3(6у-4)= 7-18у+12=5-18у
№3
0,5х-4 и 0,6х-3 х=5
0,5*5-4= -1,5 ≤ 0,6*5-3=0
№4
х=2/3
6,3х-4-3(7,2х+0,3) = 6,3х-4-21,6х-0,9= -15,3х-4,9
х= -15,3 *2/3 -4,9 = 10,2-4,9=5,31)Найдите все значения параметра b, для каждого из которых неравенство выполняется при любых действительных значениях x
(b+2)x^2 - (2b+4)x +7b +3 < 0
2) Упростите выражение:
(1+ ctg2x ctg x) / (tg x + ctg x)
Решение: Что такое параметр? Вообще, нелегко ответить на этот вопрос. Чем отличается параметр от переменной? Часто бывает так, что школьник видит подобные уравнения и неравенства и думает "а что, это неравенство с двумя переменными? Как же тогда его решать?" Поэтому разницу между параметром и обычной переменной необходимо уяснить. Переменная - это то, к чему мы привыкли, когда имеем дело с уравнением или неравенством. Мы не знаем, что из себя представляет этот самый икс. Наша задача - его найти. А чем отличается параметр? В нашем неравенстве есть переменная x и параметр b. Параметр - это ЧИСЛО. Оно не задано. Его обозначили буквой b. Представьте себе обычные уравнения или неравенства с обычными числами. Эти числа взяли и заменили на какие-то буквы. Вот это и есть параметры. Значение переменной ещё нужно находить. А значения параметра уже известно. Просто можно считать, что параметр b - это абстрактное число. Оно не задано, но мы знаем, что оно есть. Нам не важно, чему оно равно, важно, что это ЧИСЛО. Так что это никакая не вторая переменная, а лите буквенная запись числа. В отличие от обычной переменной, значение которой нам надо найти, значение параметра нас не интересует.
В задачах обычно просят всё же найти значение параметра, при котором будут выполняться какие-то условия, например, уравнение будет иметь столько-то корней, решением неравенства будет интервал какой-то длины и так далее.
У нас есть задача. Есть неравенство. b- здесь параметр. Спрашивается, при каких b неравенство выполняется для любых x. Просто представьте себе. Вместо b мы подставляем нужные значения, получаем обычное неравенство относительно x, решением которого будут все числа. Вот такие b нам и надо отыскать. Такие числа, при которых полученное "нормальное" неравенство будет иметь решением все числа. Кстати, обратите внимание, что если вместо b мы будем подставлять какие-либо значения будут получаться различные неравенства каждый раз, имеющие свои решения и свои свойства. Вот нам надо отыскать такие b, при подстановке которых получается то неравенство, о котором спрашивается. Думаю, теперь формулировка должна быть понятной.
Смотрим на неравенство. Воспринимаем b как обыкновенное число. Очень похоже на квадратное неравенство. Но оно ли это? Дело в том, что мы не знаем значение параметра, оно вполне может быть таким, что при x^2 коэффициент обращается в 0. Так что рассматриваем сначала этот случай.
1)Пусть b + 2 = 0. Отсюда b = -2. Это b может подходить нам, а может и не подходить, проверяем его, подставляя в неравенство и решая полученное.
$$ 0 x^{2} - 0x - 11 < 0 \\ -11 < 0 $$ - да это совершенно верное неравенство. Обратите внимание, что выполняется оно ВСЕГДА, то есть. при всех x. Так что b = -2 - то, что нам нужно, не забудем в конце дописать её к ответу. Кстати, в этом случае у нас даже не квадратное неравенство.
2)А вот теперь, когда при квадрате коэффициент у нас отличен от 0, я имею право сказать, что неравенство у нас квадратное. Затруднение вызывает
, как в случае квадратного неравенства ответить на поставленный вопрос. Для этого надо учесть ещё одну вещь. Помните, когда мы решали неравенство методом интервалов, у нас было несколько вариантов разных, какие могут быть решения. Что мы делали тогда? Рисовали параболу(потому что квадратный трёхчлен левой части у нас задаёт параболу), ветви её направляли в зависимости от знака коэффициента при квадрате(если положителен, то ветви вверх, если отрицателен - то вниз). Затем мы заштриховывали интервал либо между корнями, либо за ними в обе стороны в зависимости от знака самого неравенства. Мы могли обратить внимание на два принципиально разных случая - направления ветвей. В этом случае решения получаются совершенно разными. Так что вот это нам и надо будет учесть. При квадрате коэффициент зависит от параметра, какой он: положительный или отрицательный? А кто его знает. Надо рассмотреть оба случая.
а)Пусть b + 2 > 0, b > -2, то есть ветви параболы задающей левую часть неравенства, направлены вверх. Теперь поиграемся с самой параболой, её точное положение мы не знаем, так что будем двигать её. Вот так, как на первых трёх фотографиях. Очевидно, что двигать её будем именно так. Это три основных случая, которые мы рассматривали тогда, когда учились решать такие неравенства. Двигать параболу по горизонтали нам смысла нет, так как множество решений зависит именно от расположения параболы относительно оси OX. Корни x1,x2 - это корни квадратного трёхчлена(помните, вначале мы находили корни левой части). Возникает вопрос. В случае направления ветвей вверх может ли быть такая ситуация, что квадратный трёхчлен отрицателен для всех x(то есть, для всех y парабола ниже оси OX). Смотрим, в первом случае наше неравенство вообще решений не имеет(вся парабола выше оси OX). Во втором случае аналогично(есть лите одна точка, где многочлен равен 0 - это x0, но точек, где парабола ниже оси OX, то трёхчлен отрицателен, нет).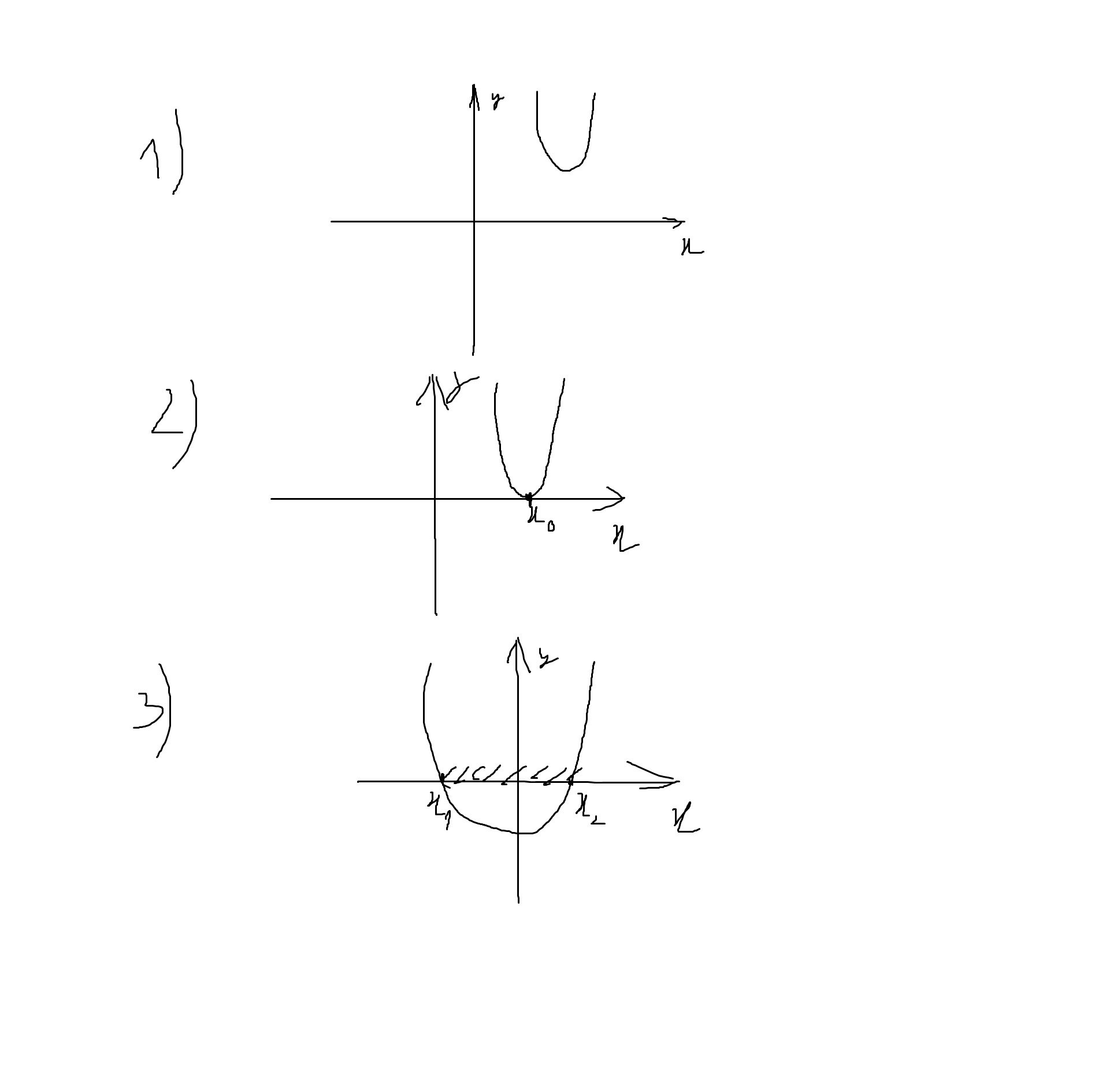
Упростите выражение √(12+2√11)+√(12-2√11)
Решение: $$ \sqrt{12+2\sqrt{11}}+\sqrt{12-2\sqrt{11}}= \\ = \sqrt{2(6+\sqrt{11})}+\sqrt{2(6-\sqrt{11})} \\ 2(6+\sqrt{11})=1+2\sqrt{11}+11=1+2\sqrt{11}+(\sqrt{11})^2=(1+\sqrt{11})^2 \\ 2(6-\sqrt{11})=1-2\sqrt{11}+11=1-2\sqrt{11}+(\sqrt{11})^2=(\sqrt{11}-1)^2 \\ =\sqrt{(1+\sqrt{11}^2}+\sqrt{(\sqrt{11}-1)^2}= \\=1+\sqrt{11}+\sqrt{11}-1=2\sqrt{11} $$√(12+2√11) + √(12-2√11) =√(1+11+2√11) + √(1+11-2√11)=√(1+√11)² + √(1-√11)²=
=|1+√11| + |1-√11| = (1+√11 )+( √11-1)=2√11
Так как 1-√11<0, то модуль |1-√11|=-(1-√11)=√11-1
№1. Упростите выражение: b^1/3 : b^²29
№2. Найдите значения выражения: log₃ (9а) если log₃ а = 0,3
№3. Вычислите: -⁵√0,016 · ⁵√-0,02
№5. Решите неравенство: 2x+14/(x+4) (x-7) ≥ 0
№6. Укажите промежуток, которому принадлежат корни уравнения: x - √2x² - 9x+5=3
Решение:1) b^(1/3)/29b^2 =1/ 29*b^(5/3)
2) log₃ (9а) если log₃ а = 0,3
log3 (9a) = log 3 9 + log 3 a = 2+ log 3 a = 2+0.3=2.3
3) ⁵√0,016 · ⁵√-0,02 = (0.016*-0.02)^(1/5) = ( -0.00032)^( 1/5 ) = -0.2
5) (2x + 14)/(x+4)(x-7) >=0
2(x+7)/(x+4)(x-7) >=0
{ x+7 >=0
{ (x+4)(x-7) >0
x >= -7
x>-4
x>7
[-7;-4) U (7;oo)
6) x-√2x^2-9x+5 = 3
√2x^2-9x+5 = x-3
2x^2-9x+5 = (x-3)^2
2x^2-9x+5=x^2-6x+9
x^2- 3x -4 = 0
D=9 +4* 1 *4 = 5^2
x=3+5/2=4
x2=3-5/2=-1
Подходит только 4
1. Упростите выражение а) (а+6)в квадрате-2а*(3-2а) б) (а-4)*(а+4)-2а*(3-а)
2. Найдите корни уравнения а) y^2 - 81 = 0; б) 9х-х в кубе=0
3. Постройте график функций y=2x-2. Определите, проходит ли график через точку (-10;-20)
4. Решите систему 5х-2y=11; 4х-y=4
5. Разность двух чисел равна 12. Одно из них больше другого в 4 раза. Найти эти числа.
6. У Толи 18 монет по 2руб и сколько-то по 5руб, всего на сумму 96руб. Сколько монет каждого достоинства у Толи?
Решение: a)a^2+12a+36-6a+4a^2=05a^2+6a+36=0
D<0 следовательно решений нет.
1.
а)$$ (a+6)^{2} -2a*(3-2a)=a^{2}+36-6a+4a^{2}=-6a+5a^{2}+36 $$
б)$$ (a-4)(a+4)-2a(3-a)= a^{2}-16-6a+2a^{2}=-6a+3a^{2}-16 $$
2.
а)$$ y^{2}-81=0\\y^{2}=81\\y=9 $$
б)$$ 9x-x^{3}=0\\x(9-x^{2})=0\\9-x^{2}=0\\x^{2}=9\\x=3 $$
3.
y=2x-2
x | 2 | 1 |
y | 2 | 0 |
Графиком функции является прямая.(ты просто отметь эти точки на графике)
Если х=-10, а у=-20 то,
у=2х-2
-20=2(-10)-2
-20=-20-2
-20=-22-неверно, значит график не проходит через точку (-10;-20)
4.
$$ \left \{ {{5x-2y=11} \atop {4x-y=4}} \right. \\ \left \{ {{5x-2y=11} \atop {-8x+2y=-8}} \right. $$
_____________
-3x=3
x=-1
$$ \left \{ {{x=-1} \atop {5x-2y=11}} \right. \\ \left \{ {{x=-1} \atop {-2y=11+5}} \right. \\ \left \{ {{x=-1} \atop {y=-8}} \right. $$
Ответ:(-1;-8)
5.
Пусть первое число х, тогда второе 4х. Разность этих чисел по условию задачи равна 12
Составляем уравнение:
4х-х=12
3х=12
х=4 - первое число.
4*4=16- второе число.
Ответ: 4 и 16.
6.
Какая сумма в двухрублевых монетах: 18*2=36руб.
Сколько денег в 5-ти рублевых монетах: 96 - 36 = 60руб.
60 : 5 = 12 монет достоинством 5 руб.
Ответ: 12 пятирублевых монет.
1) Упростите выражение a^2 - 16/a * 1/(a-4) + (4-a)/a и найдите его значение при а = 0,82) Упростите, 2√125 - 0.5√20 + 9√45 - 6√5
3) Найдите все корни уравнения 2x^2 = 90 - 7x
4) Решите неравенство 7x-2(4x-3) > 4 В ответе укажите наибольшее решение
5) Упростите выражение 6x^-5*y^7 * 1,5x^6*y^-6
Решение: 2). 2·5√5-0,5·2√5+9·3√5-6√5= 10√5-√5+27√5-6√5=30√5
5). 6х⁻⁵у⁷·1,5х⁶у⁻⁶=6·1,5х⁻⁵⁺⁶у⁷⁻⁶= 9ху
1). (а-4)(а+4) 1 4-а а+4 4-а
--------------- · ---------- + ------------ = ---------- + -------- =
а (а-4) а а а
а+4+4-а 8 8
= --------------- = --------- ( при а = 0,8) = -------- = 10
а а 0,8
4). 7х-2(4х-3)>4
7х-8х+6>4
-х>4-6
-x>-2
x<2
x∈(-∞; 2)1. Найдите корни уравнения 6х^2-х-35=0
2. Упростите выражение 1дробь х-у * 1 дробь х+у * (х дробь у-у дробь х).
3. Решите неравенство 14+4(3-х)<-2(5-х)
Решение: 1)6x2-x-35=0d=(-1)2-4*6*(-35)=1+840=841
x1=(1+29)/12=15/6
x2=(1-29)/12=-3/2
1. Найдите корни уравнения 16-х^2=0
2. Решите систему уравнений {2х+у=1
х+2у=-7
3. Запишите число 0,0056 в стандартном виде.
4. Из формулы р=0,8h+10 выразите h.
5. Упростите выражение (а-2)^2-3a(a-1)
6. В выражении 3ху^2-6ху вынесите за скобки общий множитель.
7. Вычислите (3^-4)^2*3^5
Решение: 1.
-x²=-16
x²=16
x=4 x=-4
Ответ:-4; 4
2. 2х+у=1 => y=1-2x
x+2(1-2x)=-7
x+2-2x=-7
-x=-9
x=9
y=1-2*9=1-18=-17
Ответ: 9, -17
3. $$ 0,0056= \frac{56}{10000} = \frac{7}{1250} $$
4.$$ p=0,8h+10 \\ 0.8h=p-10 \ h= \frac{p-10}{0.8} = \frac{5(p-10)}{4} $$
5. (а-2)^2-3a(a-1) = a² - 4a + 4 -3a² +3a = -2a² - a+4
6. 3ху^2-6ху = 3xy(y-2)
7. $$ (3^{-4} )^{2} *3 ^{5} = 3^{-8} * 3^{5} = 3^{-3} = \frac{1}{27} $$1. Найдите корни уравнения sin(x+пи/4)+cos5x=0, удовлетворяющие условию |x|< пи/5 2. Вычислите: sin50* (1-2cos80*) 3.Упростите выражение: sin^2(a)+sin^2(b)+2sin(a)*sin(b)*cos(a+b)
Решение:1.cos(П/4 -х) + cos5x = 0, (так как sina = cos(П/2 -а))
По формуле суммы косинусов:
2cos(П/8 +2х) * cos(П/8 -3х) = 0
Получим две группы решений:
П/8 +2х = П/2 + Пк и 3х -П/8 = П/2 + Пк
х = 3П/16 + Пк/2 х = 5П/24 + Пк/3
Нам задан промежуток: (-П/5; П/5).
Давая к разные целые значения выберем подходящие корни:
х1 = 3П/16 (<П/5) при к = 0 х3 = -П/8 (>-П/5) при к= -1
х2 = -5П/16 (>-П/5) при к = -1 (5П/24>П/5 - не подходит)
Ответ: -5П/16; -П/8; 3П/16.
2.
$$ sin50(1-2cos80)=cos40(1-2(2cos^240-1))=cos40(3-4cos^240) $$
$$ =\ -\ (4cos^340\ -\ 3cos40)= -cos(3*40) =-cos120=0,5 $$
Здесь мы воспользовались формулой косинуса утроенного угла.
Ответ: 0,5.
1) Найти корни уравнений: х^2-4<0 х^2+4<0 х^2-4>0 x^2+4>0
2) Решите неравенство: 2х-5<9-6(х-3)
3) Упростите выражение при с=1,2 6с-с(в квадрате) с(в квадрате) ______ : __________ 1-с 1-с
Решение: 1) Решаем неравенства:x^2-4<0
переносим как в уравнении числа в правую часть неравенства,меняя знаки,как в уранении
x²<4
x<2
x<-2
чертим ось, ставим эти координаты, штрихуем, и на пересечение штриховки, выписываем ответ : х принадлежит(-∞; -2)
дальше с другими неравенствами проделываем то же самое
2) 2x-5<9-6(x-3)
2x-5<9-6x+18
2x+6x<28+5
8x<33 (:8)
x<4,125
опять чертим ось, ставим число, потом штрихуем, выписываем ответ:(-∞;4,125)
