неравенства »

решите неравенство методом интервалов

  • Решите неравенство используя метод интервалов
    А) (х+8)(х-4)> 0
    Б) х-5
    ----- <0
    х+7


    Решение: $$ (x+8)(x-4)>0 $$
    ----------()----------()------->
      -8 4
    Подставим 0 в неравенство (так как он лежит между -8 и 4). Получаем отрицательное число, а значит нами подходит два интервала: (-∞;-4)U(8;+∞)

    $$ \frac{x-5}{x+7} <0 $$
    ----------()--------------()------>
      -7 5
    Подставим 0 в неравенство (так как он лежит между -7 и 5). Получаем отрицательное число, а значит нами подходит интервал (-7;5)

    Вместо скобок () должны стоять выколотые (то есть пустые внутри) точки на прямых

  • решите неравенство , используя метод интервалов (х+8)(х-4)>0


    Решение: (х+8)(х-4)>0
    (х+8)>0            (х-4)>0
    X>-8                 x>4
    Вычерчиваем две прямые и выделяем промежутки:x>-8 ,  x>4
    Ответ:(4;плюс ∞)





    Раскрываем скобки x2-4x+8x-32>0
    x2+4x-32>0
    y=0  y=x2+4x-32
    x2+4x-32=0
    D=144
    1x= -4+12:2=4 2x=-4-12:2=-4
    Строим график функции x и отмечаем точки (-4:4)
    Находим интервалы для x и получаем ответ
    x принадлежит от ( -∞:-4) и(4:∞)

  • Решите неравенство, используя метод интервалов: (х+3)(х-4)(х-6)<0


    Решение: Н.ф.:-3; 4; 6

    ответ: (-бесконечности;-3); (4; 6)

    X+3=0 x-4=0 x-6=0
    x=-3 x=4 x=6
    Строим точки на числовой оси.
    В промежутке между точками -3 и 4 брем точку 0 и подставляем ее вместо х.
    В первых скобках получ. положительное значение (+).Во вторых (-).И в третьих (-). Минус на минус = плюс.Плюс*плюс= +.
    Значит, в этом промежутке (-3;4) знак +.
    Т.к. нам надо найти значение меньше 0, то берем интервалы со знаком (-). (После нахождения пляса знаки в интервалах чередуем).
    Получаем ответ:
    (-∞;-3)
    (4;6)
    или так
    х<-3
    4<х<6

  • Решите неравенство, используя метод интервалов.(x+8)(x-4)(x+1)>0.


    Решение: Х+8=0; х-4=0; х+1=0;⇒х=-8;х=4; х=-1. Три критические точки!!! Чертим числовую прямую, отмечаем пустыми кружками на ней эти координаты! Берём число из множества (-∞;-8), вставляем в искомое неравенство, получаем отрицательное число. Потом любое число из (-8;-1), получаем "+", из (-1;4), получаем "-", из (4;+∞) , получаем "+".

    Ответ:положительным неравенство будет на интервале (-8;-1) U (4;+∞)

  • Решите неравенство используя метод интервалов

    (х+8)(х-4)(х+1)>0


    Решение: Часть слева равна 0 если х = -8, 4, -1

    Строим координатную прямую.

    Проверим положительное или отрицательное х, если подставить значение, большее чем 4

    (5+8)(5-4)(5+1)=78.

    (х+8)(х-4)(х+1)>0

    Находим корни среди нулей функции.

    х₁=-8 х₂=4 х₃=-1

    Расставляем на координатной прямой по возрастанию : -8, -1, 4.

    Делим на интервалы. Правый крайний интервал "+", Дальше чередуется : -, +, -.

    Знак неравенства показывает, что нам нужны значения больше 0, значит выбираем интервалы с "+".

    Ответ: х∈(-8;-1)U(4;+∞)

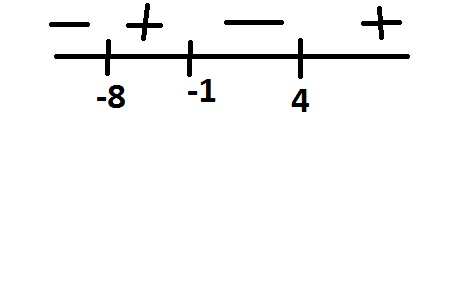
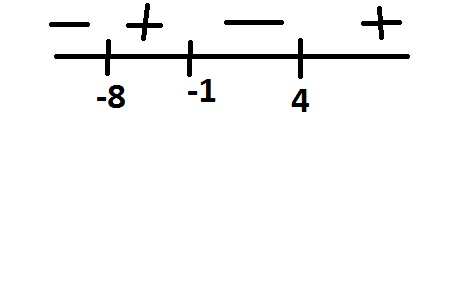
    Часть слева равна если х - - Строим координатную прямую. Проверим положительное или отрицательное х если подставить значение большее чем - . х х- х Находим корни сред...
1 2 3 > >>