неравенства »
решите неравенство методом интервалов - страница 3
Решите неравенство методом ИНТЕРВАЛОВ
1)(5-х)(х+6)<0
2)(х-10)(15-х)> ЛИБО РАВНО 0
3)(7-х)(11+х)>0
4)х-2.7/х-3 ( и все это < ЛИБО РАВНО 0)
5)Х-7/х-1 (и все это > ЛИБО РАВНО НУЛЮ)
6)х(х-18)(х+1.7)<0
Решение: 1)(5-х)(х+6)<0 2) (х-10)(15-х)≥0
5-х=0 х+6=0 х-10=0 15-х=0
х=5 х=-6 х=10 х=15
- + - - + -
------ -6----------- 5--------------- ---------- 10 -------------- 15--------
х∈(-∞; -6) и (5; +∞) х∈[10;15] или 10≤х≤15
3) (7-х)(11+х)>0 4) [(х-2,7)/(х-3)]≤0
7-х=0 11+х=0 х-2,7=0 х-3=0
х=7 х=-11 х=2,7 х=3
- + - + - +
------- -11 ------------ 7 ----------- --------- 2,7----------- 3 -------------
х∈(-11; 7) или -11<х<7 х∈[2.7; 3) или 2,7≤х<3
5) (х-7)/(х-1) ≥0 6) х(х-18)(х+1,7)<0
х-7=0 х-1=0 х=0 х-18=0 х+1,7=0
х=7 х=1 х=18 х=-1,7
+ - + - + - +
--------- 1 ------------ 7----------- -------- -1,7 ------- 0 ------------- 18 ---------
х∈(-∞; 1) и [7; +∞) х∈(-∞; -1,7) и (0; 18)Решите неравенство методом интервалов (x(2x-x^2)(2-x^2)(x^2-5x+6))/((4+x^2)(x^3-8)(x^2+x+200))<=0
Решение: X(2x-x²)(2-x²)(x²-5x+6)/(4+x²)(x³-8)(x²+x+200)≤0
x²(2-x)(√2-x)(√2+x)((x-2)(x-3)/(4+x²)(x-2)(x²+2x+4)(x²+x+200)≤0
x≠2
x²(x-2)(x-√2)(x+√2)(x-3)/(4+x²)(x²+2x+4)(x²+x+200)≤0
4+x²>0 при любом х,x²+2x+4>0 при любом х,x²+x+200>0 при любом х т.к.D<0⇒
x²(x-2)(x-√2)(x+√2)(x-3)≤0
x=0 x=2 x=√2 x=-√2 x=3
+ - - + _ +
------------------------------------------------------
-√2 0 √2 2 3
x∈[-√2;√2] U (2;3]
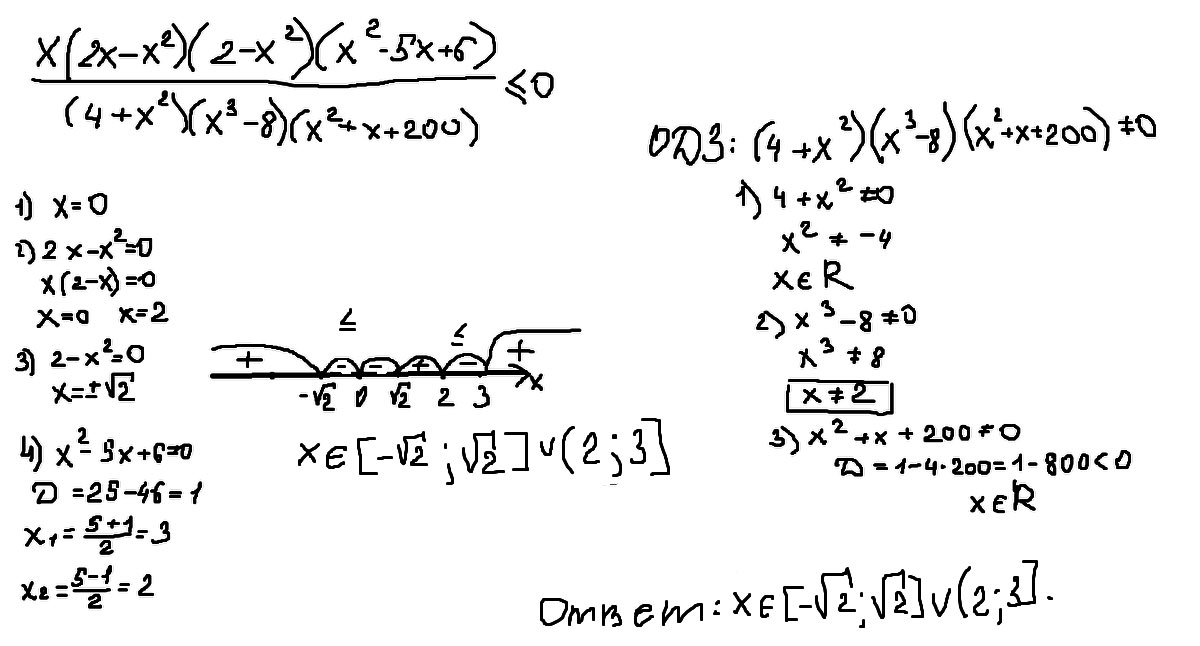
Решите неравенство методом интервалов (2-3x) (3-2x) (2x-1)≤0
Решение: Находим нули функции
у=(2-3x) (3-2x) (2x-1)
Решаем уравнение:
(2-3x) (3-2x) (2x-1)= O
2-3х = 0 или 3-2х = 0 или 2х-1 = 0
-3х = -2 -2х = -3 2х = 1
х= 2/3 х=3/2 х=1/2
Отмечаем эти точки на числовой прямой и расставляем знаки функции. Знаки чередуются:
- + - +
----------------[1/2]------[2/3]-----------------------[3/2]--------------
Ответ. [1/2; 2/3] U [3/2;+∞)решить неравенство методом интервалов x ²(х-3) (х+6)<0
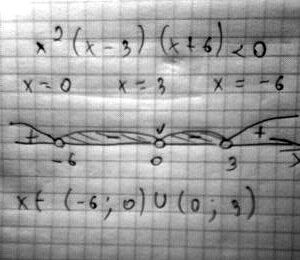
Решение: находим нули функции и изображаем на числовой прямойx ²(х-3) (х+6)<0
x² = 0, x - 3 = 0, x + 6 = 0
x = 0 x = 3 x = -6
x ∈ (-∞; -6) - положительный знак;
х ∈ (-6; 0) - отрицательной
х ∈ (0; 3) - отрицательной
х ∈ (3; +∞) - положительной.
Поскольку " < ", то х ∈ (-6; 0) U (0; 3)
решите неравенство методом интервалов -х*2+11х+60≥0
Решение: -х*^2+11х+60≥0x^2 -11x-60 <= 0
D=361
x1=15, x2=-4
(x-15)(x+4) <= 0
+ - +
_____________ -4____________15________________
Ответ: [-4; 15]
Решение в приложенном файле
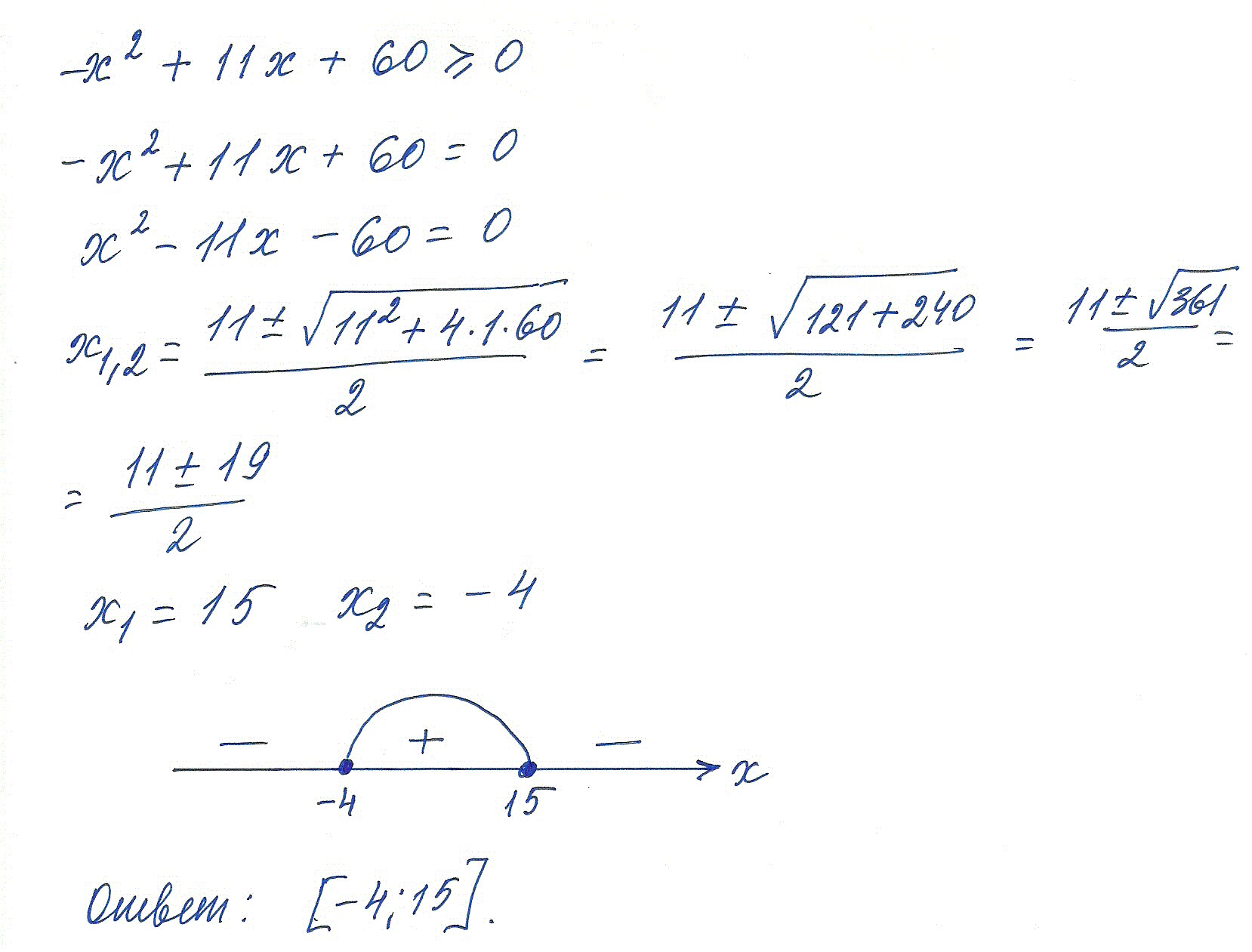

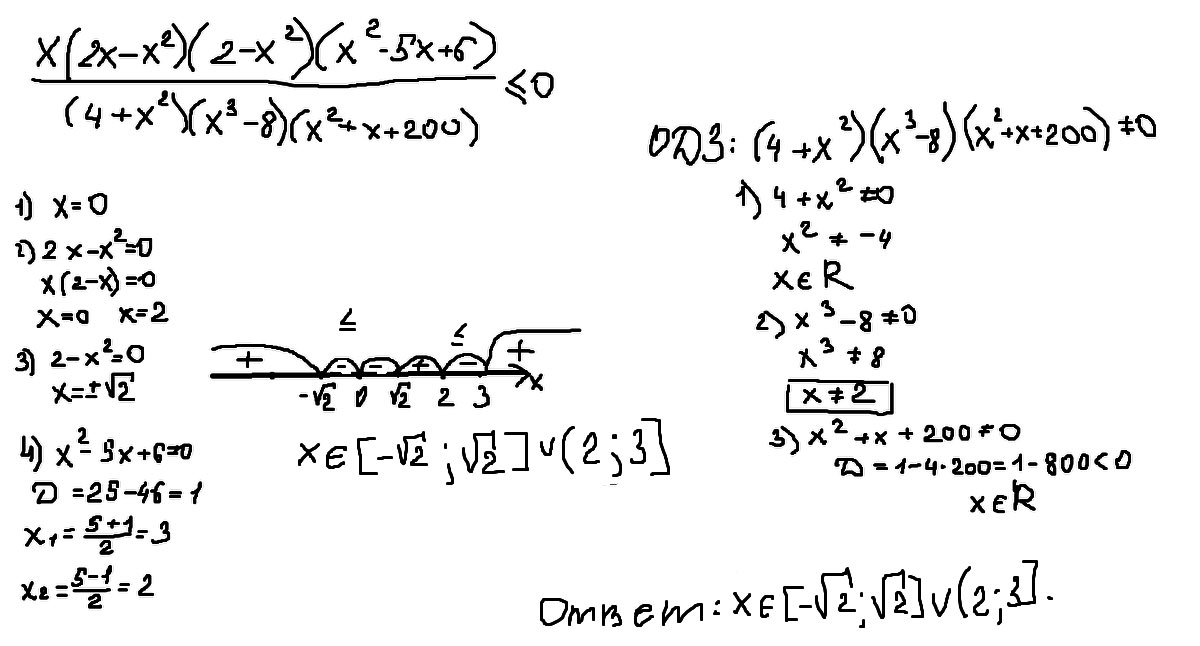

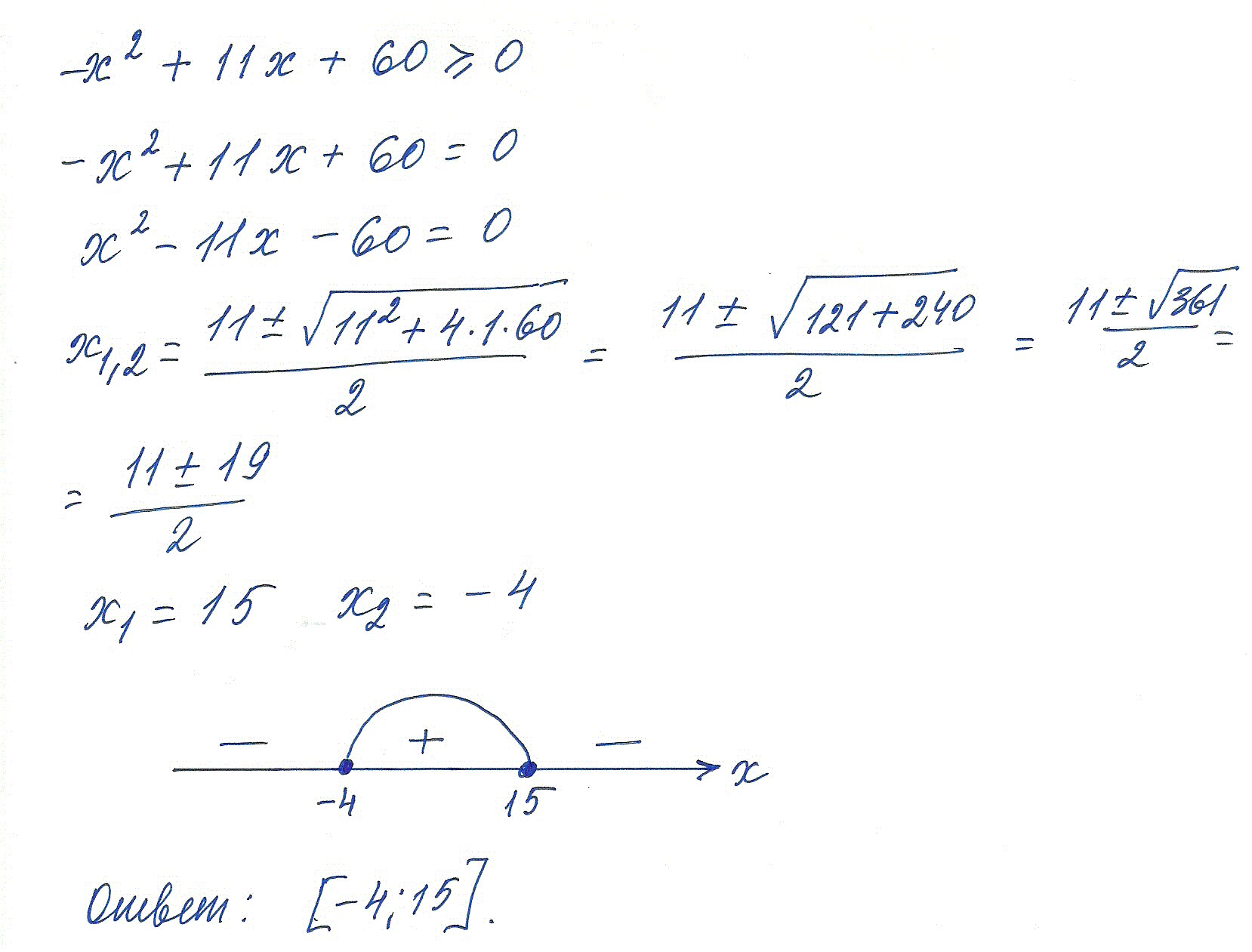
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...