решите неравенство методом интервалов - страница 5
Решить неравенство методом интервалов (x-2)(2x+3)/4-x ≥0
Решение: $$ \frac{(x-2)(2x-3)}{4-x} \geq 0 $$
Чтобы решить методом интервалов нужно сначала найти точки, для этого:
1. x-2=0 ⇒ x=2
2. 2x+3=0 ⇒ $$x= \frac{-3}{2} $$
3. $$ 4-x eq 0 ⇒ x eq 4 $$
Знаки расставляем так:
Подставим в неравенство -2, получим ≈4,6 ⇒ на интервале знак +
Дальше знаки чередуются.
Т.к. нам нужен промежуток, где ≥ 0, то получим ответ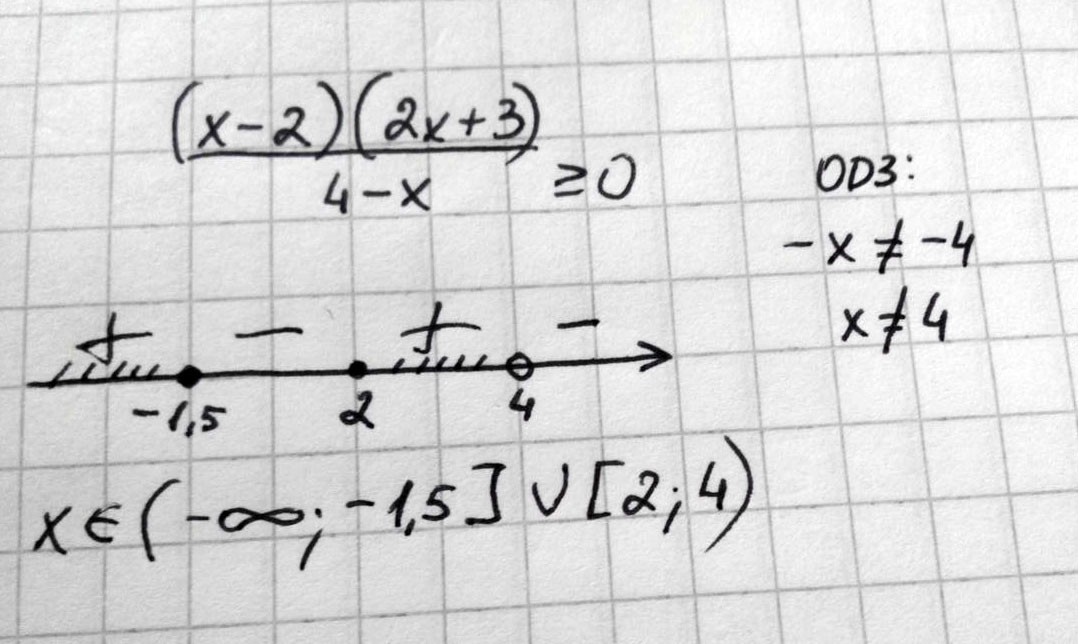
Решить неравенство методом интервалов:\((x^2-16)\cdot \sqrt x+3<0\)
Решение: (x²-16)·√(х + 3) < 0ОДЗ х + 3≥ 0 откуда х≥-3
(x²-16) = 0
х = ±4 х = -4 не входит в ОДЗ
х + 3 = 0
х = -3
разбиваем числовую прямую на интервалы точками х = -3 и х = 4 и определяем знаки неравенства в интервалах
f(x) =(x²-16)·√(х + 3)
f(0) < 0
f(5) > 0
- +
-3----------- 4 -------------
По картинке видим, что решением неравенства является
х∈(-3; 4)
границы открыты, т.к. заданное неравенство строгое
Решить неравенство методом интервалов: х(х-1)(х+2)>или равно 0
Решение: Нули функции 0, 1,-2Чертите прямую, отмечаете на ней эти точки
от минус бесконечности до -2 включая будет знак минус
от -2 до 0 включая конечные точки знак плюс
от 0 до 1 включая конечные точки знак минус
и от 1 включая до плюс бесконечности будет знак плюс
нашему уравнению удовлетворяет от минус 2 включая до 0 включая и от 1 включая до плюс бесконечности)
x(x-1)(x+2)=0 разбиваете на 3 уравнения.1:х=0 2:х-1=0 х=1 3:х+2=0 х=-2. чертите числовую прямую.отмечаете корни уравнений в порядке возрастания.точки закрашены.отмечаете знаки(после 1 +,а левее просто чередуете их)если надо объяснить почему так знаки.говорите,что за х бралось число 100.все х получились положительные.значит первый знак +.остальные чередуются.вот и все:)ответ: [-2;0],[1,+∞)
Решить неравенство методом интервалов 8x-3<x в квадрате +3
Решение: $$ 8 x-3< x^{2} +3 $$8x-3-x^2-3<0
-x^2+8x-6<0 домножаем на -1 знак неравенства меняется на противоположный
х^2-8x+8>0
D=100 x1=9 x2=-1 отмечаем на числовой оси числа 9 и -1 соединяем змейкой начинаем со знака + и ответ выписываем согласна тому где + ответ:(-бесконечности до -1) и (от 9 до + бесконечности
Решить неравенства методом интервалов. 1. -(х - 3) (х + 5) > 0 2. (x + 1) (3-x) ( x - 2)≤ 0
Решение: Разделите обе части уравнения на -1, при этом знак неравенства меняем на противоположный (x-3)(x+5)<0, отмечаем на числовой прямой точки 3 и -5, ищем знаки на каждом из промежутков. знаки будут такими(считая слева направо) +,-,+.решением будет интервал от -5 до 3 не включая концы промежутка.
второе неравенство аналогично, вынесем минус из второй скобки, получим
-(x+1)(x-3)(x-2)<=0. меняем знак неравенства (делим на -1)
x+1)(x-3)(x-2)>=0 отмечаем на числовой прямой точки -1,3,2. ищем знаки на каждом из промежутков (слева направо знаки будут такими) -,+,-,+. решением будут 2 промежутка: от -1до 2 и от 3 до +бесконечности.

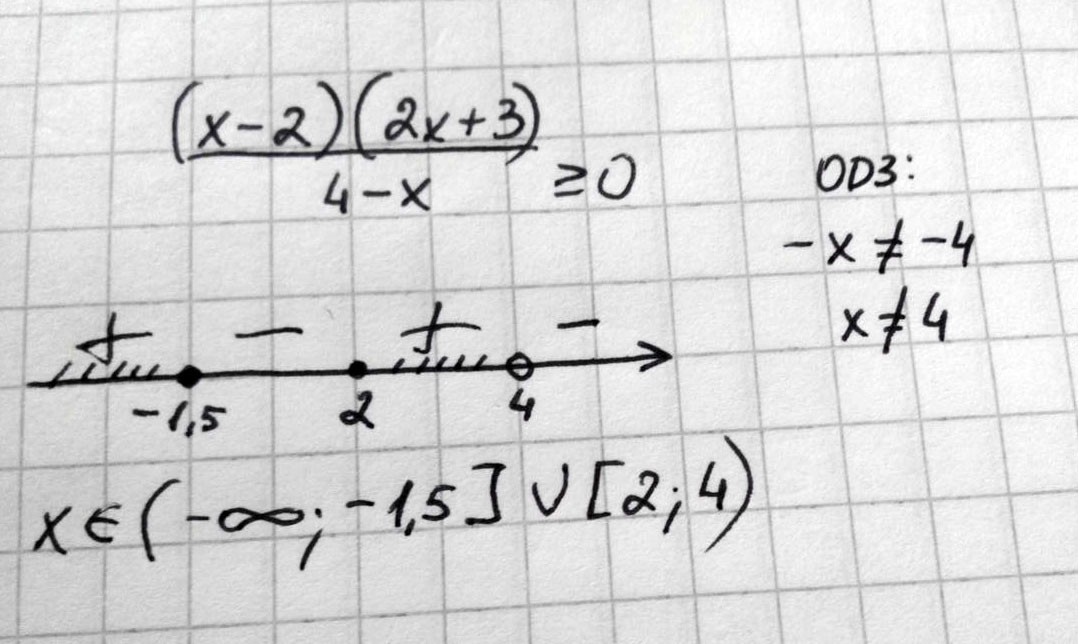
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...