неравенства »

решите неравенство методом интервалов - страница 4

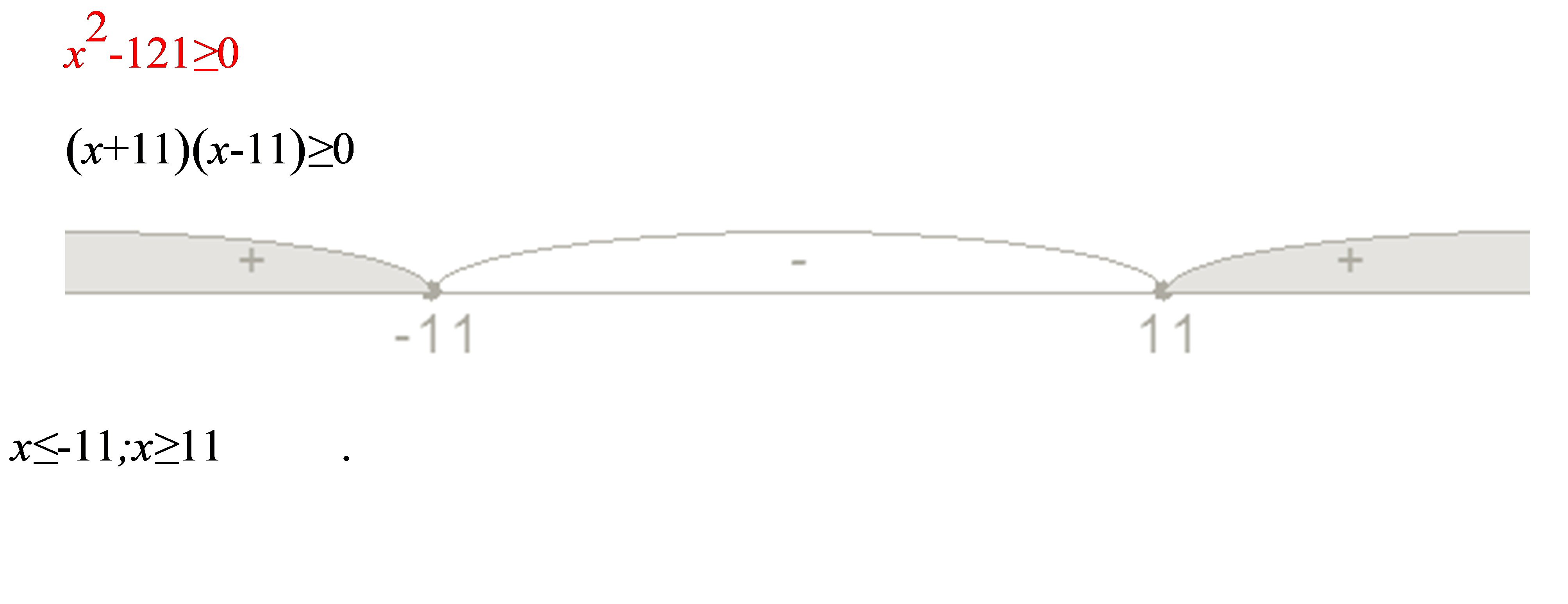
  • Решите неравенство методом интервалов х*2-121 ≥ 0


    Решение: x^2 -121>=0

    (x-11)(x+11) >=0

        +                           -                           +

    _________  -11______________11_______________

    (- бескон; -11] объединённое [11;+ ∞)

    x - x- x                                -                             - - бескон - объедин нное...

  • Решите неравенство методом интервалов:x^4-15x²-16≤0


    Решение: X⁴ - 15x² - 16 ≤ 0,
    Решаем биквадратное уравнение
    x⁴ - 15x² - 16 = 0
    Замена переменной
    х²=t  
    x⁴=t²
    t² - 15t - 16 = 0
    D=225+4·16=289=17²
    t=(15-17)/2=-1  или  t=(15+17)/2=16
    обратная замена
    х²=-1 - уравнение не имеет решений
    х²=16  ⇒ х=-4  или х=4
    Отмечаем корни на числовой прямой сплошным кружком  или квадратными скобками [ ]
    --------------------------[-4]----------------[4]-------------------
    Находим знак на [4;+∞) например при х=10
    10⁴-15·10²-16=10000-1500-16>0
    Ставим знак "+" и знаки чередуем
       +  -  +
    --------------------------[-4]----------------[4]-------------------

    Решение неравенства -4 ≤ х ≤ 4
    Ответ. [-4;4]



  • Решить неравенство методом интервалов:(2х+7)*(3х-4)*(х+5)≥0


    Решение: (2х+7)*(3х-4)*(х+5)≥0
    находим нули функции
    2х+7 = 0
    2х = -7
    х = -3.5
    3х-4 = 0
    3х = 4
    х = 1 1/3 
    х+5 = 0
    х = -5
    _-_-5__+__-3.5_-__1 1/3_+___
    х Э [-5;-3.5] v [1 1/3; +]


    $$ (2x+7)(3x-4)(x+6) \geq 0 \\ 2x+7=0\\2x=-7\\x=-3.5\\3x-4=0\\3x=4\\x= 1\frac{1}{3} \\ x+5=0\\x=-5 $$


      - + - +
    -----------------|------------------------|-----------------------|------------> x 
      -5 -3.5 1 1/3

    x ∈ $$ [-5;-3.5]U[1 \frac{1}{3} ;+ \infty ) $$



  • Решите неравенство методом интерваловх-3/х+1>5


    Решение: $$ \frac{x-3}{x+1}>5\\\frac{x-3}{x+1}-5>0\\\frac{x-3-5x-5}{x+1}>0\\\frac{-4x-8}{x+1}>0\\\frac{4x+8}{x+1}<0 $$
    Найдём нули неравенств:
    $$ \begin{cases}4x+8=0\\x+1=0\end{cases}\Rightarrow\begin{cases}x=-2\\x=-1\end{cases} $$
    Нанесём точки на числовую прямую и определим знаки (см.рис.).
    Неравенство выполняется на промежутке (-2; -1).
    Ответ: $$ x\in(-2;\;-1) $$

  • Решить неравенство методом интервалов:
    а) x^3-16x>0
    б) $$ (3x-5)/(x^2+3x) \leq 0 $$


    Решение: x(x^2-16)>0
    x(x+4)(x-4)>0,
    В знаменателе всегда выкалываем точки,т.к. на 0 нельзя делить.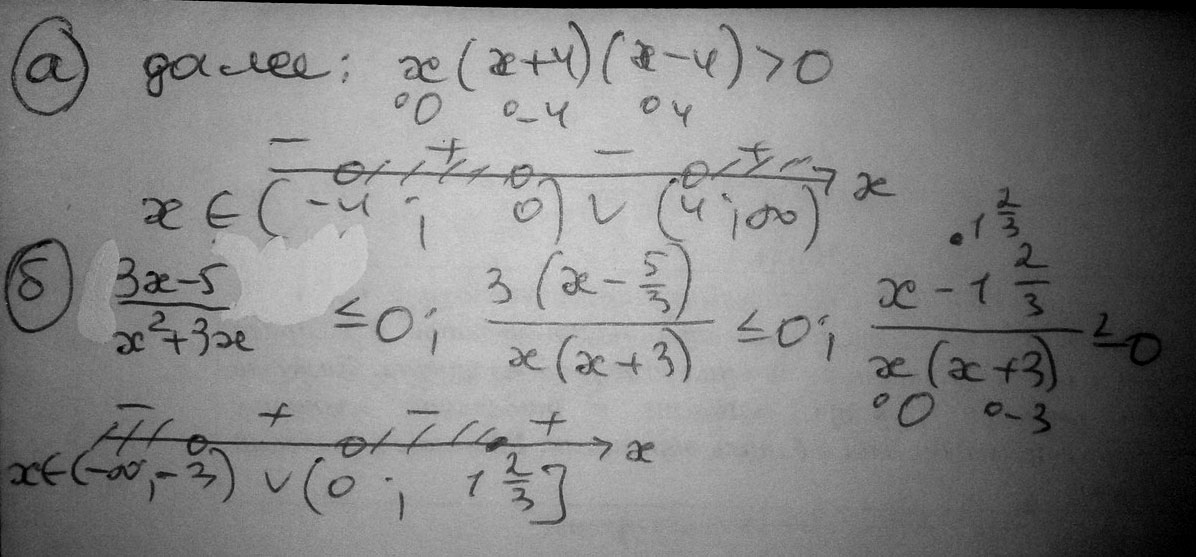

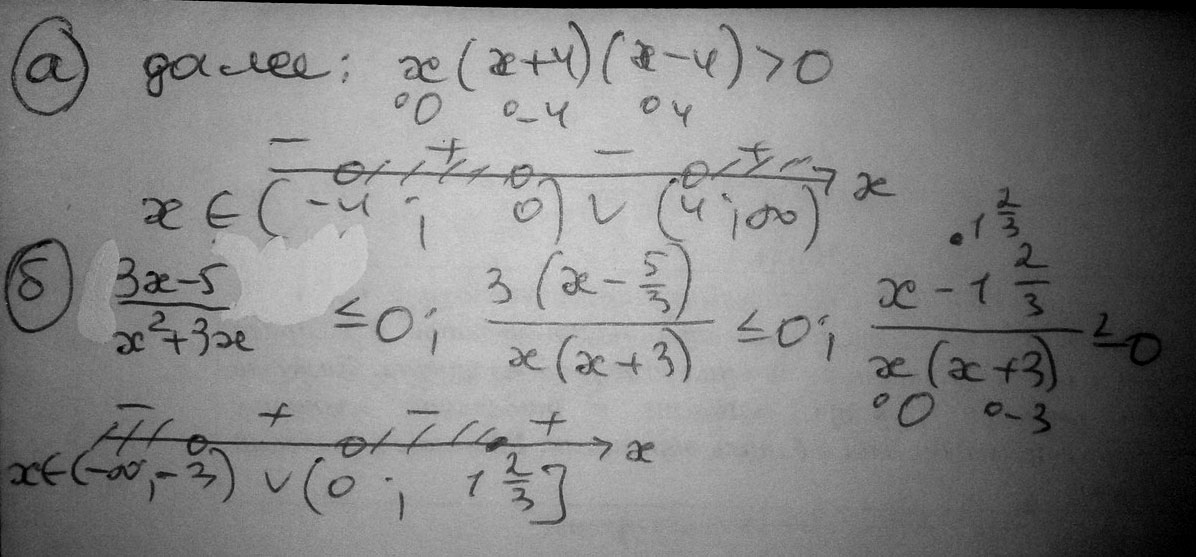
    x x - x x x- В знаменателе всегда выкалываем точки т.к. на нельзя делить....

<< < 234 5 6 > >>