неравенства »

решите неравенство методом интервалов - страница 2

  • Решите неравенство,используя метод интервалов 2x^2-x-15=0


    Решение: Дискриминант равен: 1+4*2*15=121, значит дискриминант равен 11. Х1=-5/2, Х2=3, рисуете прямую Ох, отмечаете на ней точки Х1, Х2, рисуете "змейку" расставляете знаки: слева-направо: + - +, и потом смотрите по своему неравенству, если у тебя знак больше то выбираете интервалы с плюсом, если меньше с минусом! И точки будут незакрашенные если у тебя строгое неравенство, а если не строгое то закрашенные. Строгое это когда больше или меньше, а не строгое: больше или равно нулю, меньше или равно нулю! И в ответе скобки круглые если строгое, квадратные если не строгое!

  • 1) Решите неравенство,используя метод интервалов

    (x+8)(x-5)>0

    (x-14)(x+10)<0

    2) Решите неравенство

    x(x+1)(x+5)(x-8)>0


    Решение: 1)
      ------- -8------------- 5-------------
      + - +
    х∈(-∞; -8)∪(5; ∞)
     
    ------- -10------------14------
      + - + x∈(10;14)

    2)
      ------ -5---------- -1----------- 0---------- 8---------
      + - + - +

    x∈(-∞; -5)∪(-1; 0)∪(8;∞)

  • Решить неравенство, используя метод интервалов: ( х + 2 ) ( х -5)>0


    Решение: 1. Нули неравенства - $$ x=-2 $$ и $$ x=5 $$
    Расставляем знаки, подставляя числа из промежутков в неравенство
    Ответ: $$ x \leq -2 $$ и $$ x \geq 5 $$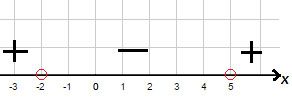

    . Нули неравенства -  x - и x Расставляем знаки подставляя числа из промежутков в неравенствоОтвет   x leq - и  x geq...

  • Решить неравенство, используя метод интервалов:

    (× + 8) (х - 5) > 0

    (x - 14) (x + 10) < 0

    (x + 25) (x - 30) < 0

    (x + 6) (x- 6) > 0


    Решение: 1.х2-5х+8х-40>0                                 3.х2-30х+25х-750<0

    x2+3x-40>0                                              х2-5х-750<0

    Д=3*3-40*4*1=169                                     Д=-5*-5-4*-750*1=3025

    х1=-3+13/2=5                                           х1=5+55/2=30

    х2=-3-13/2=-8                                           х2=5-55/2=-25

    ответ:(5;до бесконечности)                      ответ:(-25;до бесконечности)

    2. х2+10х-14х-140<0

    х2-4х-140<0                                      4.х2-6х+6х-36>0

    Д=-4*-4-4*(140)*1=576                        x2-36>0

    х2=4-24/2=-10                                   x-6=0    x+6=0

    ответ:(-10,до бесконечности)    x=6        x=-6  ответ:(6;до бесконечности)

  • Решите неравенство методом интервалова)
    (x+3)(x-4)(x-6) <0
    б)
    5x+1 деленное на x-2 < 0


    Решение: А) 1. -3,4,6 - нули
    2.располагаем эти числа на координатной прямой
    3. ответ: (-∞;-3)
    б) 1. умножаем обе части неравенства на (х-2)
       получаем: 5х-1<0
    2. решаем получившееся неравенство:
    5х<-1
    х<-0,2
    НО! х не равен 2. т.к при х=2 знаменатель=0
    Ответ: (-бескон; -0,2)

<< < 12 3 4 > >>