неравенства »
решите неравенство методом интервалов - страница 6
1) Решить систему уравнений \( \left \{ {{x-2y=2} \atop {xy=12}} \right. \)
2) Решить неравенство, используя метод интервалов (x+3)*(x+5)*(x-2) > 0
Решение: $$ 1) \left \{ {{x-2y = 2} \atop {xy=12}} \right. \\ \left \{ {{x = 2 + 2y} \atop {(2+2y)y=12}} \right. \\ 2y + 2y^2 = 12 \\ 2y^2 + 2y - 12 = 0 |: 2 \\ y^2 + y - 6 = 0 \\ D = 1 + 24 = 25 \\ y_{1,2} = \frac{-165}{2}; y_1 = 2; y_2 = -3 \\ x = 2 + 2y \\ x_1 = 2 + 2y_1 = 2 + 2 * 2 = 6 \\ x_2 = 2 + 2y_2 = 2 + 2 * (-3) = -4 $$
Ответ: (6;2);(-4; - 3)
$$ 2) (x+3)(x+5)(x-2) < 0 \\ (x+3)(x+5)(x-2) = 0 \\ x + 3 = 0; x_1 = -3 \\ x+5 = 0; x_2 = -5\\ x - 2 = 0; x_3 = 2 $$
См. рис.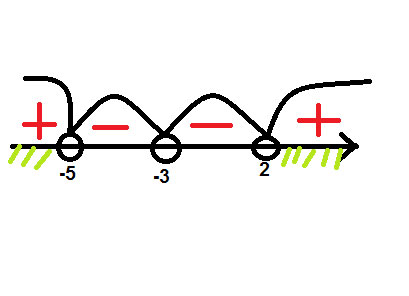
Метод интервалов, решите неравенства
(2x-3)(x+1)>0
Решение: 2X - 3 =0;⇒ x = 1,5;
x+1 =0; ⇒ x = - 1.
на прямой отмечаем эти точки(х= -1 и х=1,5), получается 3 интервала, рисуем + - + над ними и выбираем те, где плюс.
ответ х∈( - ∞: -1) ∨ ( 1,5; + ∞)Решите неравенство используя метод интервалов x-5деленое на x+7<0
Решение: Рассмотрим функцию y = (x - 5)/(x + 7)
Нули функции: x - 5 = 0
x = 5
Область опр: x + 7≠0
x ≠ -7
Отметим обе точки на числовой прямой и определим знаки функции на каждом интервале:
____+_____°____-____°_____+______>
- 7 5
y<0 при x∈( - 7 ; 5 )
Это ответРешите неравенство используя метод интервалов:
а) (x+8)(x-4)(x+1)>0
б) (6-x)(3x+12) (< или =) 0
Решение: То что я знаю:
1) 1
2)1(x+8)(x-4)(x+1)>0
x+8=0
x=-8
x-4=0
x=4
x+1=0
x=-1
(x+8)(x-4)(x+1)>0, то [-8;-1];[4;+∞]
2)(6-x)(3x+12)=<0
6-x=0
-x=-6/(-1)
x=6
3x+12=0
3x=-12
x=-4
(6-x)(3x+12)=<0, то [-4;6]
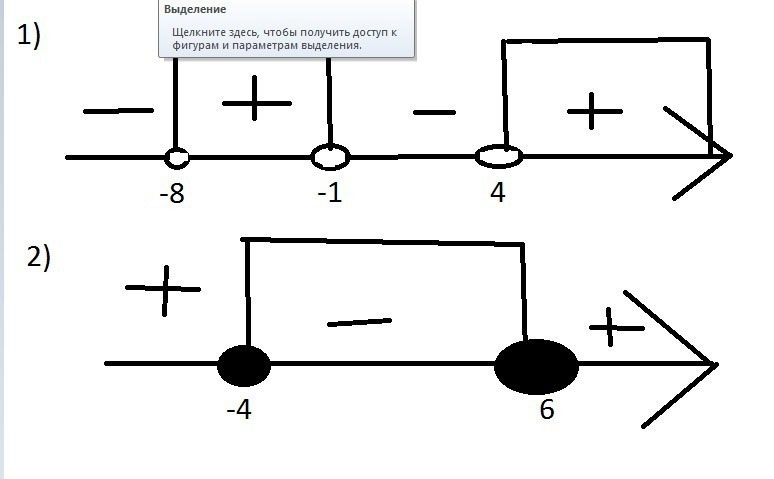
Решите неравенства, используя метод интервалов
1) x^2+12x+80<0
2)x+3/x-8 >0
Решение: 1) D=144-240=-176
D<0
x^2+12x+80 всегда строго больше 0;
Ответ: нет решений
2) x+3/x-8 >0
см. рисунок
Ответ:(-∞;-3) ∪ (8;+∞)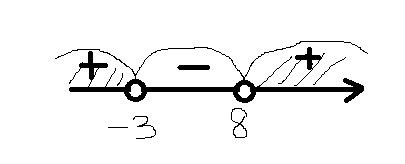




 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...